Donner une définition précise ? Pas si simple !

Au XVII^e siècle, suite à « son » invention de la géométrie analytique (voir article "Une notion géométrique insaisissable", § Vers l'époque moderne), René Descartes sait déterminer les tangentes à une courbe géométrique donnée. Son contemporain et correspondant Pierre de Fermat (vers 1601 ; 1665), en utilisant une notion de « nombres infiniment petits », le fait pour une multitude de courbes, géométriques comme mécaniques. Prenons le folium de Descartes, une courbe qui a pour équation x³ + y³ – 3xy = 0. Il s’agit d’un exemple de courbe géométrique, dans la terminologie de Descartes, qui ne provient pas d’une construction mécanique. Avec la terminologie moderne, c’est une cubique, c’est-à-dire une courbe algébrique de degré 3. Bien que jugé difficile par Descartes, le calcul des tangentes à cette courbe fut réalisé par Fermat de manière élégante.

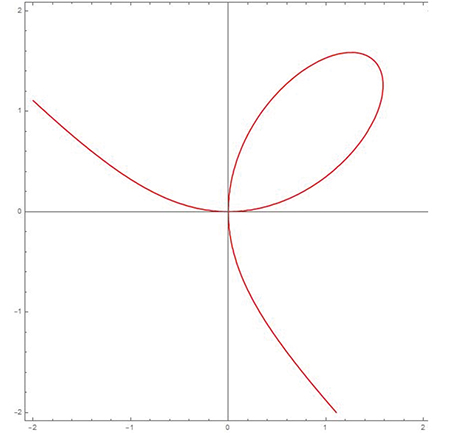
Le folium de Descartes.

C’est alors le début du calcul infinitésimal, qui va se développer avec Isaac Newton (1642–1727) et Gottfried Wilhelm Leibniz (1646–1716). Pierre-Simon Laplace (1749–1827) affirmera d’ailleurs dans son Programme : « L’un des plus féconds rapprochements que l’on ait faits dans les sciences est l’application de l’algèbre à la théorie des courbes. La recherche de ces propriétés a conduit à l’analyse infinitésimale, dont la découverte a changé la face des mathématiques. »

L’analyse et l’ère classique

Avec les nouvelles techniques permises par l’avènement du calcul infinitésimal, on sait dorénavant étudier et calculer de nombreuses caractéristiques des courbes, essentiellement locales : tangente, normale, rayon et centre de courbure en un point… Apparaissent alors les courbes définies comme un arc paramétré : c’est l’image d’un intervalle de \( \mathbb{R}\) , ensemble des nombres réels, dans le plan habituel, le plan  \( \mathbb{R}^2\) , par une application continue  : \( \overset{\rightarrow}{\varphi} : I\to \mathbb{R}^2\) .

Cela permet de définir beaucoup de courbes mais certaines passent au travers des mailles du filet : l’hyperbole possède ainsi deux morceaux (composantes connexes) et ne peut donc pas être l’image par une application continue d’un intervalle de  \( \mathbb{R}\) , qui, lui, est constitué d’un seul morceau.

Une hyperbole.

Par contre, avec cette définition, d’autres objets mathématiques sont aussi des courbes mais nous surprennent, comme ces rosaces où seul l’intervalle de définition I diffère d’une courbe à l’autre. Elles sont définies par  \( x=\sin(t\sqrt{2})\times\cos t,\,\, y=\sin(t\sqrt{2})\times\sin t.\)    On imagine l’aspect de la courbe quand I devient encore plus grand ! Sans doute bien loin de la représentation géométrique que l’on se fait habituellement d’une courbe.

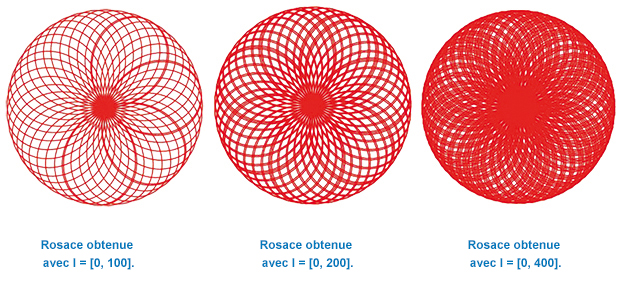
Si l’on veut éviter certaines complications, comme la non-existence de tangente en certains points, on demande à l’application  \( \overset\to{\varphi} \) , dans la définition de la courbe comme arc paramétré, d’être dérivable, voire de classe  \( \mathrm{C}^n\)  avec n ≥ 1 (c’est-à-dire que l’on impose que les dérivées jusqu’à l’ordre n soient continues), ou même de classe C^∞ (indéfiniment dérivable). On peut aussi demander que  \( \overset\to{\varphi} \)  soit injective pour éviter les points multiples. Mais on exclut alors des courbes comme la lemniscate de Bernoulli.

Après les travaux de Leibniz et de Jean Bernoulli (1667–1748), le génial mathématicien Leonhard Euler (1707–1783) précise la notion de fonction d’un point de vue formel et non plus géométrique. À une fonction \( f:I\to\mathbb{R}\)  est alors associée sa représentation graphique : la courbe d’équation y = f (x). On retrouve là une notion bien connue de tous les lycéens mais qui ne recouvre pas, loin s’en faut, tous les exemples de courbe…

Représentation graphique de la fonction f avec  \( f(x) = \sin(x^2+x)-\frac{x^2}{8}.\)

La topologie entre en jeu

La notion d’arc paramétré est plus générale mais, ne recouvrant pas, elle non plus, tous les exemples de courbes, une autre approche a été tentée, avec l’avènement de la topologie, au cours du XIX^e siècle. En fait, une courbe n’est qu’une ligne droite que l’on a « déformée de manière continue », d’où une définition possible : une courbe est une partie du plan homéomorphe à une droite. Mais ceci ne convient pas non plus car alors le cercle n’est pas une courbe !

Il faut nécessairement passer à une approche locale : on appelle courbe un sous-ensemble du plan dont tout point possède un voisinage homéomorphe à la droite. Cela revient à dire qu’en « zoomant suffisamment » en tout point de la courbe, ce que l’on voit est un segment de droite. Mais, avec cette nouvelle définition, il n’y a pas de point multiple car, dans ce cas, on verrait au moins deux segments de droite se coupant… et donc, à nouveau, certaines courbes sont exclues, comme la lemniscate de Bernoulli.

On pourrait alors définir une courbe comme un sous-ensemble du plan dont tout point possède un voisinage qui est la réunion finie de parties homéomorphes à la droite. Les points multiples sont maintenant possibles. Mais alors les rosaces précédentes ne sont pas des courbes, de même que la cochléoïde. Étudiée en 1685 par John Wallis (1616–1703), la cochléoïde est définie par  \( \Big(x=\frac{\sin t}{t}\,\,{\rm{et}}\,\, y=\frac{1-\cos t}{t} \Big)\)  pour t différent de 0, et par (x = 1 et y = 0) si t = 0. C’est le lieu de l’extrémité d’un arc de cercle mobile conservant une longueur constante dont l’autre extrémité, O, est fixe et tangente à une droite donnée, l’axe (Ox).

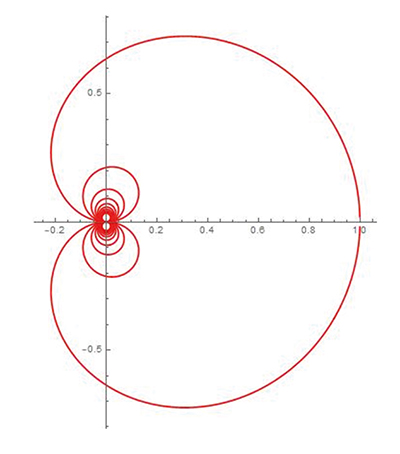
Repartons d’une autre idée. Une courbe algébrique est définie par une équation P (x, y) = 0, où P est un polynôme de deux variables. On pourrait généraliser cela en définissant une courbe comme le sous-ensemble du plan défini par l’équation f (x, y) = 0, où f serait une fonction continue de deux variables, voire de classe C¹ (au sens où toutes les dérivées partielles existent et sont continues) ou même C^∞ (les dérivées partielles de tous ordres existent et sont continues). Malheureusement, avec une telle définition, on obtiendrait aussi des courbes bien loin de l’idée que l’on s’en fait. Par exemple, toute bande serait une courbe ! En effet, en prenant 

\( f(x,y)=\left\{ \begin{array}{ll} 0 & \mathrm{si}\ 0\leq x<1 \\ -x & \mathrm{si}\ x<0 \\ -1+x & \mathrm{si}\ x\geq 1 \end{array} \right.\)

on obtient la représentation graphique ci-dessous.

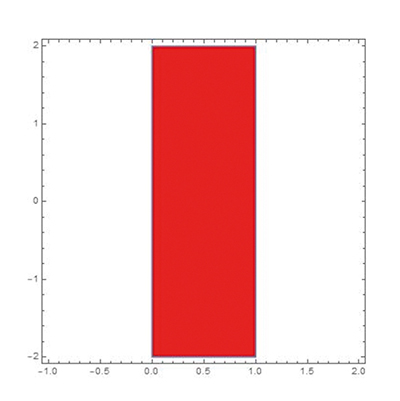
La fonction f est bien continue. Il est relativement facile de « lisser » f et de la remplacer par une fonction C^∞. Une piste de plus à abandonner…

Autant l’étude globale des courbes algébriques définies par P (x, y) = 0 a fait l’objet de travaux nombreux et profonds, après ceux de Descartes et de Newton, y compris dans d’autres espaces que le plan habituel, autant l’étude globale des courbes définies par f (x, y) = 0, où f est de classe C¹, est relativement récente et nécessite des concepts élaborés. Une des raisons est le fait que les courbes algébriques de degré inférieur ou égal à n forment un espace vectoriel de dimension finie, ce qui n’est absolument pas le cas des courbes de classe C¹.

L’ère moderne

La recherche d’une définition générale pour une courbe s’est encore aggravée avec l’introduction, à la fin du XIX^e siècle et au cours du XX^e siècle, d’exemples encore plus atypiques, par exemple la courbe de Peano ou le flocon de von Koch.

Giuseppe Peano (1858–1932) a défini « sa » courbe en 1890 comme exemple de courbe continue qui remplit intégralement le carré [0, 1]² sans jamais passer deux fois par le même point. Elle est la limite d’un processus dont voici, ci-dessous, les quatre premières étapes. Henri-Léon Lebesgue (1875–1941) a perfectionné en 1904 cette construction pour obtenir une courbe qui remplit, elle aussi, tout le carré mais qui, de plus, possède une tangente en « presque tous » les points !

Premières étapes de construction de la courbe de Peano.

Le mathématicien suédois Helge von Koch (1870-1924) a défini en 1904 son fameux flocon, premier exemple d’une courbe fractale (voir les Fractales, Bibliothèque Tangente 18, 2019). On part d’un triangle équilatéral. À chaque étape, on divise chaque côté en trois segments de même longueur. En utilisant celui du milieu, on construit un triangle équilatéral tourné vers l’extérieur. On enlève la base. Et on recommence. Le flocon de von Koch est la courbe obtenue en répétant ce processus indéfiniment. Comme pour la courbe de Peano, il est impossible de la tracer mais on peut s’en faire une idée en regardant les premières étapes de la construction. C’est une courbe continue mais il n’existe de tangente en aucun point : tous les points du flocon de von Koch sont « anguleux »… De plus, en un certain sens technique, sa « longueur » est infinie !

Premières étapes de construction du flocon de von Koch.

Au vu de la difficulté à définir ce qu’est une courbe, on ne sera pas étonné de l’écart qui existe entre l’énoncé suivant (le fameux théorème de Jordan, qui semble évident visuellement) et sa démonstration, qui nécessite d’avoir suivi un cursus mathématique très avancé. 

Une courbe plane continue et fermée ne se recoupant pas (sans point multiple) divise le plan en deux parties dont elle est la frontière : un intérieur et un extérieur.

L’énoncé est évident pour un cercle ou une ellipse. Il l’est déjà moins dans le cas de la figure suivante : peut-on dire facilement si un point choisi au hasard est à l’intérieur ou à l’extérieur de cette courbe ?

La démonstration de Camille Jordan (1838–1922) figure dans la deuxième édition de son fameux Cours d’analyse, publié en 1893. Si la démonstration est relativement difficile dans le cas où la courbe est continue, elle est beaucoup plus abordable avec l’hypothèse supplémentaire que la courbe est de classe C².

Finalement, définir une courbe, ce n’est peut-être pas si simple que cela et ce n’est sans doute pas le hasard si beaucoup de mathématiciens évitent de donner une définition générale !