Les distributions :

Les économistes s’intéressent volontiers à l’évolution temporelle de grandeurs. Ils se demandent comment les variations de certaines d’entre elles, privilégiées (qu’ils qualifient d’endogènes), dépendent des variations d’autres (appelées exogènes). Par exemple, on peut étudier quelle pourrait être l’influence d’une modification du taux d’imposition sur le niveau du revenu disponible des ménages.

Dans le cas le plus simple, on ne considère, au temps t, qu’une seule grandeur endogène y (t) (par exemple, le niveau des revenus) et une seule variable exogène i (t) (comme le taux d’imposition). Mathématiquement, y (t) est l’image de i (t) par une fonction f qui traduit la dépendance en question ; on dispose dès lors de l’égalité y (t) = f (i (t)). Cette fonction f peut aussi être interprétée comme un opérateur qui, au cours du temps, agit sur une fonction d’entrée, appelée une impulsion, pour fournir une fonction de sortie, baptisée une réponse.

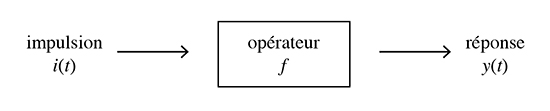
Transmission de l’influence au sein d’un système économique.

C’est quoi la réponse ?

Comme l’économie est contrôlée par des agents, une impulsion se ramène essentiellement à une décision adéquate ; ainsi, le gouvernement décide l’imposition d’une certaine taxe. Suivant l’objectif poursuivi, la décision considérée peut n’agir qu’en un seul instant ou présenter un caractère plus permanent, être déterministe ou aléatoire… Par souci de simplicité, attardons-nous uniquement sur le cas, idéalisé, d’une impulsion instantanée, prise au temps t = 0, qui fournit une réponse elle aussi instantanée et d’intensité unitaire.

Déjà, comment la réponse peut-elle être modélisée ? Admettons donc que la fonction de sortie possède une valeur nulle avant l’instant initial t = 0, puis prend la valeur constante, égale à 1, pour tout t ≥ 0. Il s’agit de la représentation graphique de la fonction indicatrice de l’ensemble des réels positifs. Cette fonction H admet plusieurs noms : fonction échelon unité, fonction marche d’escalier, fonction de Heaviside… On a H (x) = 0 si x < 0, et 1 si x ≥ 0.

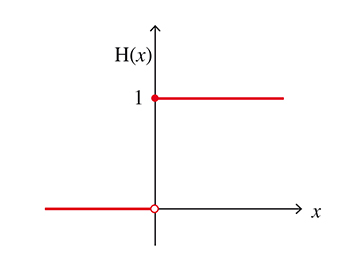
La fonction de Heaviside H.

Le physicien britannique Oliver Heaviside (1850–1925).

H est définie en tous les réels ; elle présente en x = 0 une discontinuité sous la forme d’un « saut fini », puisque ses valeurs passent brusquement de 0 à 1. Selon les applications, on peut laisser H (0) indéfini ou lui donner la valeur 1/2. Les physiciens ont l’habitude de représenter graphiquement H par une courbe continue ; cette représentation n’est plus celle d’une fonction (au sens des mathématiciens), puisqu’elle permet à H de prendre en x = 0 n’importe quelle valeur comprise entre 0 et 1.

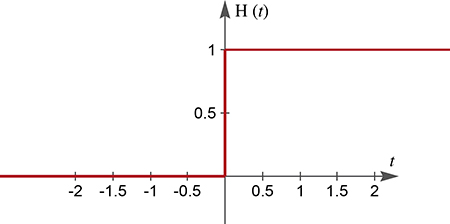
Cette représentation fournit une visualisation d’une « fonction généralisée »,
ou distribution en termes techniques.

Modélisons l’impulsion à partir de ce que l’on connaît sur la réponse H. À cet effet, intéressons-nous à la variation de la réponse, ou plus précisément au taux  \( \frac{\Delta H}{\Delta x}\)  pour une variation Δx de la variable x. Comme on s’intéresse aux impulsions et aux réponses instantanées, on souhaite connaître le taux de variation instantané ; celui-ci est donné par la limite de  \( \frac{\Delta H}{\Delta x}\)  lorsque Δx tend vers 0, ce qui correspond classiquement à la dérivée de H (x) par rapport à la variable x… pour autant que la fonction en question soit dérivable !

Or, si la fonction H est dérivable en chaque réel x non nul (où elle présente une dérivée nulle), elle n’est pas dérivable en x = 0 puisqu’elle n’y est pas continue. Ainsi, l’impulsion est nulle en tout réel différent de 0. De plus, en x = 0, elle devrait prendre une « valeur suffisamment grande » pour donner une réponse unitaire.

Pour résoudre pareil problème, le physicien britannique Paul Adrien Maurice Dirac (1902–1984) a introduit une « fonction », qui porte son nom et est souvent notée d : on pourrait la définir informellement comme étant « partout nulle, sauf en x = 0 où elle prend une valeur infinie », de sorte que son intégrale sur l’ensemble de tous les réels est égale à 1. Mais il n’est pas possible de trouver une fonction réelle f qui, comme δ, serait nulle partout sauf en 0 et dont l’intégrale \( \int^{+\infty}_{-\infty}f(x)dx\)  serait égale à 1 ; en effet, cette intégrale (au sens de Riemann comme de Lebesgue) vaut nécessairement 0. On ne peut donc pas présenter la « fonction » de Dirac dans le cadre des fonctions réelles.

Des dérivées généralisées

 Il est néanmoins possible de se faire une idée intuitive de δ en considérant une impulsion constante pendant une très courte période, mais de cumul (correspondant à la réponse) unitaire. On fait ainsi appel à une impulsion  \( i_\varepsilon (x)\) représentée graphiquement par un rectangle, dont la base horizontale est l’intervalle  \( [-\varepsilon /2,\varepsilon /2]\) et la hauteur mesure (à partir de l’axe des ordonnées) \( 1/\varepsilon\) , de sorte que son aire est bien égale à 1.

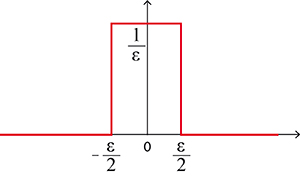
Une impulsion quasi instantanée.

Si  \( \varepsilon\) diminue, la hauteur du rectangle augmente, la largeur diminue, tandis que l’aire reste égale à 1. Si \( \varepsilon\)  devient infiniment petit, la « partie observable » du rectangle se confond avec le demi-axe positif des ordonnées. C’est pourquoi il n’est pas rare que l’on représente graphiquement  \( \delta\) par le schéma suivant. En l’abscisse x = 0, la présence d’une flèche verticale de hauteur 1 rappelle que toute l’impulsion est concentrée au temps initial et fournit une réponse unitaire.

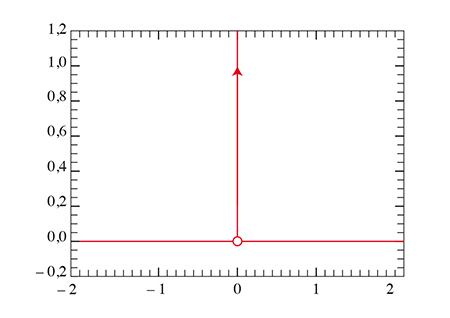
La distribution de Dirac.

Bien entendu, \( \delta\)  n’est pas une « vraie » fonction pour les mathématiciens ; il s’agit en fait d’une « fonction généralisée », c’est-à-dire une distribution. Par ailleurs, il existe une généralisation du concept de dérivée qui s’applique aux distributions ; elle permet de montrer que la « dérivée au sens des distributions » de H coïncide bien avec  \( \delta\) .

Comment donc montrer, au moins intuitivement, que la dérivée (au sens des distributions) de la fonction H de Heaviside est précisément la distribution  \( \delta\)  de Dirac ? En encadré se trouve un exemple élémentaire qui permet déjà d’aborder graphiquement la question de l’approximation de H par des fonctions H_n qui sont, elles, dérivables.

Lorsque le paramètre n croît, la représentation graphique de H_n « se rapproche » de celle de H, tandis que celle de H_n’ ressemble « de plus en plus » à une impulsion de Dirac. En effet, lorsque n est infiniment grand, la partie observable de H_n se confond avec la fonction de Heaviside H, tandis que celle de la fonction H_n’ coïncide avec l’impulsion de Dirac  \( \delta\) .

[encadre]

Une approximation de H par des fonctions dérivables

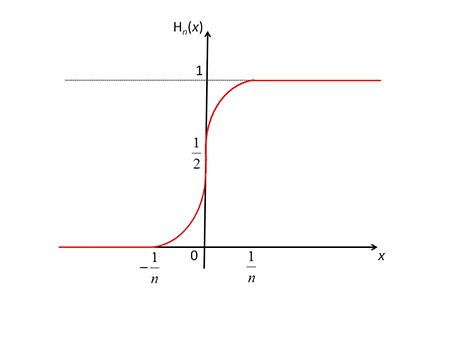
Comme la fonction H n’est pas partout dérivable en 0, essayons d’approcher géométriquement sa représentation graphique par des courbes provenant de fonctions qui, elles, sont partout dérivables. La suite de fonctions ci-dessous, indicées par l’entier n, peut être utilisée : 

\( $$H_n(x)=\left \{ \begin{array}{ll} 0 \ &\mathrm{si} \ x< -\frac{1}{n},\\ \frac{(nx+1)^2}{2}\ &\mathrm{si} \ -\frac{1}{n}\leq x\leq 0,\\ \frac{-(nx-1)^2 +2}{2}\ &\mathrm{si} \ 0< x\leq \frac{1}{n},\\ 1 \ &\mathrm{si} \ x> \frac{1}{n}.\\ \end{array} \right. $$\)

Ces fonctions sont partout dérivables. Leur représentation graphique se compose de portions de droites horizontales (pour | x | > 1 / n) et de portions de deux paraboles (la première tourne sa concavité vers le haut, et la seconde vers le bas). Les deux branches de parabole se raccordent parfaitement (avec la même tangente) entre elles en x = 0, avec l’axe horizontal en x = – 1 / n, et avec la droite horizontale d’ordonnée y = 1 en x = 1 / n.

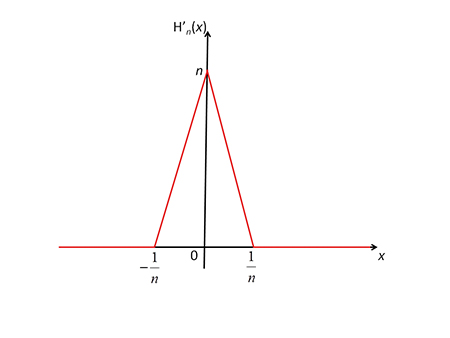
Les dérivées H_n’ de ces fonctions sont données par H_n’(x) = 0 si | x | > 1 / n, H_n’(x) = n (nx + 1) si – 1 / n < x < 0, et H_n’(x) = – n (nx – 1) si 0 < x < 1 / n. Ce sont des expressions qui sont partout continues ; elles sont affines par morceaux. Le maximum de H_n’ vaut n et l’aire du triangle délimité vaut 1, ce qui se traduit par l’égalité

\( \int^{+\infty}_{-\infty}H'_n(x)dx=1.\)

Dites-le avec des distributions

Cette modélisation, même rendue rigoureuse par un traitement mathématique approprié, n’est pas encore suffisante puisque les distributions doivent être indéfiniment dérivables. Il convient dès lors d’affiner notre exemple en travaillant avec une fonction indéfiniment dérivable d_n qui soit nulle pour | x | > 1/n, qui présente un maximum en 0 et qui soit telle que

   \( \int^{1/n}_{-1/n}d_n=1.\)  

Une telle fonction est telle que d_n (0) tend vers l’infini avec n et permet de se représenter la distribution \( \delta\) .

En définissant h_n (x) par l’aire sous le graphe de d_n (t) pour t variant de  \( -\infty\) à x, autrement dit en posant

  \( h_n(x)=\int^{x}_{-\infty}d_n(t)dt,\)  

et en faisant tendre n vers l’infini, on obtient une représentation de la distribution de Heaviside H. De telles fonctions existent et peuvent être effectivement construites en utilisant par exemple la fonction exponentielle.

Pour résoudre des problèmes qu’ils rencontraient dans leurs travaux de recherche, des physiciens, tels Heaviside et Dirac, et des électroniciens ont ainsi été amenés à utiliser des sortes de fonctions qui n’obéissent pas aux règles classiques des mathématiques. Les mathématiciens ont alors considéré ces « fonctions généralisées », qui ont été appelées des distributions. Ils ont construit rigoureusement la théorie mathématique des distributions, qui se révèle fort utile dans de nombreuses situations concrètes rencontrées notamment en physique ou en théorie des signaux. Dans certains domaines, le cadre d’étude naturel n’est en fait pas constitué d’ensembles de fonctions mais d’ensembles de distributions.

Cette théorie, amorcée notamment par les travaux de Jacques Salomon Hadamard (1865–1963) ou encore de Sergueï Lvovitch Sobolev (1908–1989), a principalement été développée par le Français Laurent Schwartz (1915–2002), qui a reçu pour cela une médaille Fields en 1950. Les distributions comptent sans aucun doute parmi les objets mathématiques les plus utilisés en physique !