Discontinuités et séries de fonctions

Les séries de fonctions ont pris leur essor au XVIII^e siècle, mais ce n’est qu’au siècle suivant que des théorèmes précis ont permis de connaître leurs propriétés, en particulier d’étudier leur continuité et leur dérivabilité. Cela a permis d’étendre considérablement le nombre de fonctions mathématiques, au lieu de se restreindre à des combinaisons d’opérations algébriques sur des fonctions élémentaires comme les puissances, les racines, le logarithme, l’exponentielle ou les fonctions trigonométriques. En particulier, de nombreux exemples de fonctions qui défient l’intuition ont pu être ainsi exhibés.

Quand la somme est discontinue

On connaît l’illusion d’optique, illustrée par Maurits Cornelis Escher, d’une fontaine dont l’eau semble toujours couler et qui se retrouve… à son point de départ.

Voici un exemple de fonction périodique, continue en tout point irrationnel mais admettant un saut négatif en tout point rationnel (c’est-à-dire que la limite à droite en ces points est toujours strictement inférieure à la limite à gauche). Une fonction périodique qui décroît toujours ? L’intuition en prend un coup…

Notons E(x) la partie entière du nombre réel x et h (x) la différence x – E(x). Cette fonction (appelée partie fractionnaire et souvent notée {x}) est périodique puisque E(x+1) = E(x) + 1 ; on a donc h (x+1) = x + 1 – (E(x) + 1) = h (x). En outre, pour tout x, | h (x) | ≤ 1. Enfin, la fonction h est continue en tout point non entier mais admet un saut négatif pour tout entier ; par exemple, h (1) = 0 mais h (x) tend vers 1 quand x tend vers 1 par valeurs inférieures.

La fonction partie fractionnaire.

Posons alors, pour tout entier n > 0, f_n (x) = h (n x) / 2 ⁿ. Pour n fixé, cette fonction est de période 1/n, donc en particulier f_n (x +1) = f_n(x) ; elle admet des points de discontinuité pour tout réel x de la forme k /n (avec k un entier), avec un saut négatif de 1/2 ⁿ. Par ailleurs, on a | f_n (x) | ≤ 1/2 ⁿ, qui est le terme général d’une série convergente. On est ainsi face à une convergence normale, donc uniforme ; on en déduit que la fonction

\( \text{S} = \sum_{n\geq 1} f_n\)

est bien définie ;

S est en particulier continue aux points où toutes les fonctions  f_n le sont (donc pour toute valeur irrationnelle de la variable).

En revanche, la convergence uniforme nous assure qu’en un rationnel a de la forme k /n (avec k un entier) la fonction f_n admet un saut ; comme tous les sauts de ces fonctions sont strictement négatifs, S est discontinue en ce point et y admet elle-même un saut négatif. Plus précisément, S est continue à droite en un tel point a et

\( \text{S} (a) - \lim\limits_{\substack{x \to a \\ x<a}} \text{S}(x) < 0.\)

De plus, S est périodique, de période 1.

Ainsi, la fonction S est définie explicitement, périodique, continue en tout point irrationnel mais est discontinue aux valeurs rationnelles de la variable en effectuant à chaque fois un saut négatif !

[encadre]

La convergence uniforme

Prenons une suite de fonctions ( f_n) _n ≥1 définies sur un intervalle J de l’ensemble ℝ des nombres réels et à valeurs réelles. Pour tout entier n ≥ 1, posons S_n la fonction de I dans ℝ définie par S_n ( x) = f₁( x) + f₂ (  x) + f₃ (  x) +… + f_n ( x). Si pour tout x de J la suite (S_n(x)) _n ≥1 admet une limite (qui dépend évidemment de x), notée S(x), on dit que la série

\( \sum_{n\geq 1} f_n\)

converge simplement vers la fonction S, dès lors appelée somme des fonctions f₁, f₂, f₃…

Contrairement à une assertion de Cauchy, la continuité des fonctions f₁, f₂, f₃… n’entraîne pas celle de S. À la fin des années 1840, George Stokes et Philipp Seidel ont (indépendamment) introduit une condition supplémentaire, appelée convergence uniforme, qui permet de conclure à la continuité de la somme.

 On dit que la série

\( \sum_{n\geq 1} f_n\)

converge uniformément vers S s’il existe une suite de réels positifs (s_n ) _n≥1 de limite nulle telle que, pour tout x dans J et tout n supérieur à 1, |S( x) – S_n( x)| reste inférieur à s_n (nombre qui ne dépend pas de x).

En pratique, on procède ainsi : s’il existe une suite de réels positifs a₁, a ₂, a ₃… telle que la série

\( \sum_{n\geq 1} a_n\)

converge, et si pour tout x dans J on a | f_n(x) | ≤ a_n, alors la convergence de la série

\( \sum_{n\geq 1} f_n\)

est uniforme. Cette condition, appelée de nos jours convergence normale, n’est cependant pas nécessaire pour avoir la convergence uniforme (elle est « plus forte », mais surtout plus confortable à utiliser).

[/encadre]

L’exemple de Riemann

Encore plus déroutant peut-être. Pour un réel x, notons, comme Riemann, p_x « l’entier le plus proche » de x, puis (x) = x – p_x . Lorsque x est équidistant de deux entiers (c’est-à-dire que x – 1/ 2 est un entier), on pose (x) = 0 ; ces nombres réels sont les seuls points de discontinuité de notre fonction, par ailleurs clairement périodique.

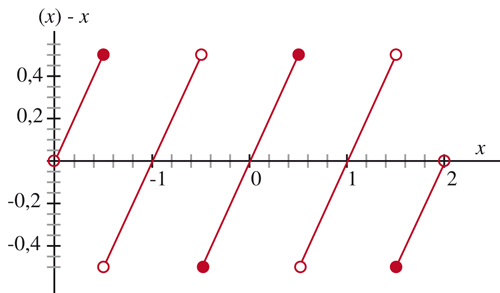
La fonction x ↦ px - x  introduite par Riemann.

Posons alors f_n(x) = (n x) / n ² pour n entier non nul. Cette fonction est continue en tout point, sauf ceux qui vérifient nx = p + 1/ 2 avec p entier, soit x = (2 p +1) / 2 n. Par ailleurs, la majoration |(x)| ≤ 1/ 2 entraîne l’inégalité | f_n (x) | = 1/ 2n ², qui est le terme général d’une série convergente. Cela montre la convergence (normale donc) uniforme de la série

\( \text{F}(x) = \sum _{n\geq 1} \dfrac{(nx)}{n^2},\)

et donc sa continuité en tout point de continuité de toutes les fonctions f_n , dont font partie tous les nombres irrationnels. En revanche, en tout point de la forme x = (2 p + 1) / 2 n où n et p désignent des entiers, la fonction n’est pas continue, comme l’a montré Riemann.

Georg Friedrich Bernhard Riemann (1826–1866). 

Les valeurs intermédiaires s’en mêlent

Le théorème des valeurs intermédiaires affirme qu’une fonction continue sur un segment [a, b] à valeurs réelles prend toutes les valeurs situées entre f (a) et f ( b). En d’autres termes, l’image par f du segment [a, b] est un intervalle, c’est même un segment. Mais qu’en est-il de la réciproque ? Elle est fausse ! En voici des exemples.

Plus précisément, convenons qu’une fonction définie sur un intervalle J, pas forcément fermé, vérifie la propriété de la valeur intermédiaire si, pour tous éléments a et b de J (avec a < b) et tout u compris entre f (a) et f ( b), il existe un réel c avec a < c < b tel que f (c) = u. Construisons alors une fonction discontinue en un point mais vérifiant tout de même la propriété des valeurs intermédiaires.

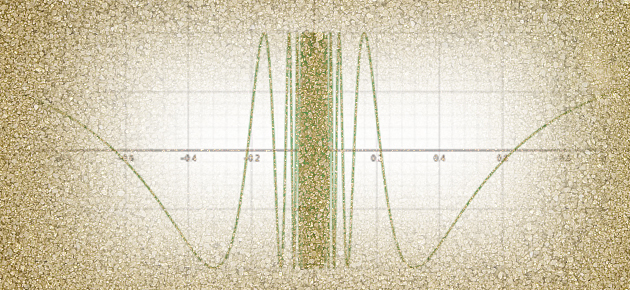
Posons f (x) = cos(1/ x) pour x non nul, et f (0) = 0. Cette fonction est discontinue en 0 et continue partout ailleurs. Aussi, pour démontrer que f vérifie la propriété de la valeur intermédiaire, il faut prendre a < 0 < b et u entre f (a) et f (b) et chercher un réel c compris entre a et b tel que f (c) = u.

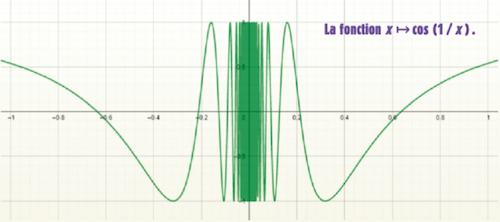
Comme, pour tout réel x, on a – 1 ≤  f (x) ≤ 1, le réel u vérifie lui aussi l’inégalité – 1 ≤ u ≤ 1. Mais la fonction cosinus est décroissante sur l’intervalle [0, π], avec
cos(0) = 1 et cos(π) = – 1. Il existe donc t compris entre 0 et π tel que cos(t ) = u. Enfin, comme la fonction cosinus admet 2π pour période, cos( t + 2 k π) = cos ( t  ) = u pour tout entier k. Posons alors x_k = 1 /( t + 2 k π ). Il vient que f ( x_k ) = f (– x_k ) = cos ( t + 2 k π ) = u. La suite (x_k )_k ≥1 tend vers 0, donc pour k assez grand, on obtient a < – x_k < x_k < b, ce qui démontre la propriété demandée.

Dans son Mémoires sur les fonctions discontinues, Gaston Darboux énonce et démontre que, comme les fonctions continues, la fonction dérivée d’une fonction vérifie la propriété de la valeur intermédiaire. Ceci permet de montrer qu’une fonction ne vérifiant pas cette propriété n’admet pas de primitive, c’est-à-dire qu’elle n’est la dérivée d’aucune fonction.

Ce résultat n’aurait évidemment aucun intérêt si toute fonction dérivée était continue. C’est pourquoi Darboux s’empresse de donner un exemple de fonction dérivable en tout point mais dont la dérivée est continue pour toute valeur irrationnelle de la variable, et discontinue pour toute valeur rationnelle (voir en encadré). Cette fonction manifestement l’émerveille et il affirme qu’« il existe des fonctions discontinues qui jouissent d’une propriété que l’on regarde quelquefois comme le caractère distinctif des fonctions continues, celle de ne pouvoir varier d’une valeur à une autre sans passer par toutes les valeurs intermédiaires ».

[encadre]

La fonction de Darboux

Pour construire une fonction dérivable mais discontinue sur un ensemble dense, Darboux pose f ( x) = x ² sin(1/ x) si x est non nul et f (0) = 0.

Ainsi, f est dérivable, avec f ’(0) = 0 et, pour x 0, on obtient f ’(x) = 2 x sin(1/ x) – cos(1/ x).

Pour |x| ≤ 1, on a | f ( x) | ≤ 1 et | f ’( x) | ≤ 3.

Posons alors

  \( \text{F}(x) = \sum _{n\geq 1} \dfrac{f(nx \pi)}{n2^n}.\)

 Darboux énonce alors le théorème suivant :

« Étant donnée une série f (x) dont tous les termes sont des fonctions continues ayant des dérivées, si la série des dérivées est uniformément convergente dans un intervalle donné et si les termes sont susceptibles d’intégration, elle représentera la dérivée de la série  f (x). »

Introduisons 

\( g_n(x) =\dfrac{f(nx \pi)}{n2^n}.\)

 Sa dérivée est 

\( g'_n(x) = \pi \dfrac{f' \big( \sin(nx \pi)\big)}{2^n} \cos (nx\pi).\)

 L’inégalité

\( \mid g'_n(x) \mid \; \leq \dfrac{3\pi}{2^n} \)

montre que la série converge uniformément et que l’on peut appliquer le théorème de Darboux.

La fonction F est donc dérivable, et sa fonction dérivée est

\( \text{F'}(x) = \sum _{n\geq 1} g'_n(x).\)

Tout point de discontinuité d’une des fonctions g_n est un point de discontinuité de F (soit tous les points x tels qu’il existe un entier positif n annulant sin(n x π), ce qui correspond à l’existence d’un entier k tel que n x π = k π, ou encore x = k /n). Comme tout nombre rationnel peut s’écrire de la sorte, la dérivée de la fonction proposée par Darboux est, suivant ses termes, « discontinue pour toutes les valeurs commensurables de x ».

[/encadre]

Le monstre inventé par Lebesgue

Terminons par une épouvantable fonction introduite en 1904 par Henri Lebesgue : non intégrable au sens de Riemann, elle devient intégrable (et d’intégrale nulle) dans la théorie qu’il a introduite quelques années plus tôt.

Henri-Léon Lebesgue (1875– 1941). 

Considérons un réel x compris entre 0 et 1, exprimé par son développement décimal propre x = 0,a₁a₂a₃ …a_n… (si le nombre est décimal, on évite le développement se terminant par une suite infinie de 9 pour lever toute ambiguïté). Si la suite de ses décimales de rang impair n’est pas périodique à partir d’un certain rang, on pose f (x) = 0 ; si cette suite est périodique à partir du rang p, c’est-à-dire de a_2p – 1, on pose
f (x) = 0, a _2p a _2p + 2 a _2p + 4…

Par exemple, si x = 0,6158742375297429762…, en supposant que les termes de rang impair soient alternativement 7 et 2 indéfiniment, alors p = 2 et on pose f (x) = 0,4359496… (ce sont les décimales de rang pair à partir de la sixième).

Prenons deux réels α et β tels que 0 < α < β < 1 ainsi qu’un réel c situé entre 0 et 1 ; on cherche un réel x compris entre α et β tel que f (x) = c. Considérons un nombre x dont les premières décimales en nombre pair, noté 2 p, le place entre α et β et complétons ce développement en prenant comme décimales de rang pair celles de c et en choisissant celles de rang impair de telle sorte qu’elles forment une suite périodique commençant au rang 2 p + 1. Alors l’image par  f du nombre obtenu est le nombre c, ce qui permet de conclure.

Il est impossible, bien sûr, de tracer le graphe d’une telle fonction ; il paraîtrait se confondre avec l’axe des abscisses…

Ainsi, l’intuition est souvent trompeuse et les fonctions que l’on manie couramment sont d’une immense régularité, même celles qui paraissent « un peu biscornues ».