
La pensée scientifique qui prit corps à la Renaissance avec Galilée et Descartes s’est employée à rechercher la régularité dans les phénomènes physique et, en parallèle, dans leur modélisation mathématique. Bien que l’hypothèse divine ne soit plus le moteur de la compréhension du monde, la croyance en Dieu était toujours vivace et il ne faisait aucun doute que Dame Nature répondait à Son désir de beauté, qualité qui se réalisait dans la régularité du monde. Cela explique peut-être pourquoi la notion de discontinuité était totalement absente de la recherche scientifique.
Dirichlet et les fonctions trigonométriques
Pour parler de fonctions discontinues, encore faut-il définir précisément la notion de fonction, mais surtout celle de continuité ! Jusqu’à la fin du XVIIIe siècle, une fonction était définie par une expression, éventuellement deux, qui se composaient de puissances, de racines, de logarithmes et se trouvaient de facto continues (voir les Fonctions, Bibliothèque Tangente 56, 2016). Le souci d’introduire une notion précise de continuité se développe au début du siècle suivant avec Bolzano et Cauchy et trouve son achèvement vers 1860 avec Karl Weierstrass et ses élèves.
Augustin Louis, baron Cauchy (1789–1857), photographié par Charles Reutlinger.

Bernard Bolzano (1781–1848).

Karl Weierstrass (1815–1897).
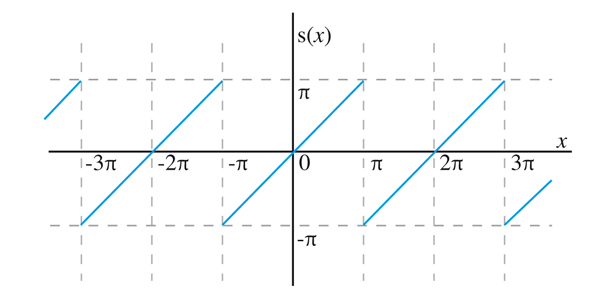
Dans les années 1810, Joseph Fourier, alors préfet de l’Isère, publie un mémoire sur la décomposition de fonctions périodiques en séries trigonométriques, c’est-à-dire comme somme (infinie) de fonctions de la forme an cos nx + bnsin nx. Son ouvrage, certes peu rigoureux, est le début de la formalisation d’une théorie qui motivera d’innombrables recherches tout au long de ce siècle ; elle permet de développer certaines fonctions élémentaires, comme la fonction x ⟼ x, sur l’intervalle ]–π, π[, reportée ensuite de manière périodique. Comme on le constate, cette fonction n’est pas continue aux raccords de ce report.

Jean Baptiste Joseph Fourier (1768–1830).
En 1822, un jeune étudiant allemand, Gustav Lejeune Dirichlet, vient parfaire ses études à Paris. Il rencontre Fourier et se passionne alors pour le nouveau domaine ouvert par son prestigieux aîné. Revenu en Allemagne, il se penche sur la convergence des séries trigonométriques, sujet sur lequel Fourier avait été très imprécis, et publie en 1828 un article dans le Journal de Crelle donnant des conditions suffisantes de convergence qui englobent de nombreuses fonctions discontinues et qui, d’après son élève Bernhard Riemann, est « le premier article ayant vraiment du fond sur le sujet ». Cela conduit Dirichlet à donner une définition de la notion de « fonction » beaucoup plus générale que ses prédécesseurs, en ces termes : « Si à chaque x correspond un unique y, alors y s’appelle une fonction de x. » Il n’est dès lors plus nécessaire d’avoir l’expression explicite de f (x) pour parler de « fonction », ce qui ouvre un champ beaucoup plus large à la construction de fonctions défiant les critères de régularité habituels. En fait, Dirichlet ne faisait que formaliser une notion qu’il utilisait déjà puisque, quelques années plus tôt, en 1829, il avait donné un exemple de fonction continue nulle part, définie par f (x) = 1 si x est rationnel et 0 sinon (voir page En Bref).

Johann Peter Gustav Lejeune Dirichlet (1805–1859).
[encadre]
Quand Abel s'oppose à Cauchy
En 1821 parait la première partie du Cours d’analyse de l’École royale polytechnique de Cauchy avec le titre Analyse algébrique. On y trouve pour la première fois une définition précise de la continuité. Le théorème énoncé au bas de la page 131 n’échappera pas à l’esprit aiguisé d’un jeune mathématicien norvégien, Niels Abel, lors de son séjour parisien en 1826.
Cauchy affirmait que lorsqu’une série de fonctions continues converge dans le voisinage d’une valeur particulière, la somme de cette série est continue en cette valeur. Dans un article publié en français en 1826, Abel écrit prudemment : « Mais il me semble que ce théorème admet des exceptions. Par exemple, la série sin x – (sin 2x) / 2 + (sin 3x) / 3 –… est discontinue pour toute valeur (2m+1) π de x, m étant un nombre entier. Il y a comme on sait beaucoup de séries de cette espèce. »
Abel avait parfaitement raison : cette fonction est égale à x /2 si x est strictement compris entre –π et π, elle vaut 0 en π, et elle est de période 2 π ; elle n’est donc pas continue au point π (et de même en tous les réels π + 2 k π avec k un entier relatif). Il faut ajouter une condition supplémentaire pour conclure à la continuité de la limite, que l’on appelle la convergence uniforme, notion introduite dans les années 1840, indépendamment, par trois mathématiciens, Philipp Ludwig von Seidel, George Gabriel Stokes et probablement Karl Weierstrass.
[/encadre]
[encadre]
La fonction de Seidel
On peut trouver des contre-exemples beaucoup plus simples au théorème erroné énoncé par Cauchy, en travaillant directement sur des suites de fonctions et non plus sur des séries. Il suffit de considérer les fonctions fn : x ⟼ x ndéfinies sur l’intervalle [0, 1]. Pour 0 ≤ x < 1, la suite (x n ) n ≥1 converge vers 0 tandis que la suite (1n ) n ≥1 est constante (égale à 1) et tend donc vers 1. La fonction limite est donc la fonction f qui est nulle sur [0, 1[ et telle que f (1) = 1 ; elle n’est donc pas continue au point 1.
Un ancien élève de Dirichlet, Philipp Seidel, remarque que les travaux de son maître sur les séries de Fourier fournissent d’innombrables nouveaux contre-exemples. Il propose par ailleurs un spécimen de type nouveau de fonction discontinue, obtenue comme limite d’intégrales de fonctions continues.
À cet effet, il pose
En posant le changement de variable u = xt, on obtient F ( x) = π / 2 si x > 0, F (x) = –π / 2 si x < 0, et on remarque directement que F(0) = 0. Ainsi, cette intégrale définie, dépendant du paramètre x, définit une fonction discontinue.
Posons alors
Les fonctions un sont toutes continues et, par la relation de Chasles généralisée, on se convainc que
On obtient alors un nouvel exemple qui met en défaut l’assertion de Cauchy.
Seidel se demande quelle « propriété cachée » pourrait permettre de conclure à la continuité de la fonction limite d’une suite de fonctions continues. Il en énonce une, bien maladroitement, mais qui correspond tout à fait à la notion de convergence uniforme.
[/encadre]
Voici Riemann et Weierstrass
Dans son cours professé à l’École polytechnique, Cauchy avait donné un sens précis à la notion d’intégrale d’une fonction continue sur un segment. Les séries de Fourier devenant un sujet d’étude très développé, les fonctions discontinues prennent une importance accrue ; mais alors, comment les intégrer ? Elles ne possèdent pas de primitive.
Bernhard Riemann s’attaque à ce problème dans un mémoire publié en 1854. Contrairement à Cauchy, qui donnait sens à quelque chose qu’on savait déjà calculer, Riemann s’attaque à définir ce que l’on peut appeler
pour des fonctions pas nécessairement continues. Sa méthode s’apparente certes à celle de Cauchy, mais il se heurte à une difficulté nouvelle : caractériser, parmi toutes les fonctions, celles pour lesquelles on peut définir une intégrale. Cette construction est connue de nos jours sous le nom d’intégrale de Riemann (voir le Calcul intégral, Bibliothèque Tangente 50, 2014). Le savant allemand exhibe alors un exemple de fonction intégrable dans sa nouvelle théorie mais possédant un ensemble dense de points de discontinuité, c’est-à-dire qu’entre deux points, « aussi près que l’on veut l’un de l’autre », on peut trouver un point de discontinuité (voir article Discontinuités et séries de fonctions, § L'exemple de Riemann).
Un autre obstacle à l’étude précise des fonctions discontinues était l’absence de construction des nombres réels. Au fond, on supposait de fait la complétude de ℝ, mais aucune définition précise n’était donnée. On doit principalement à l’école allemande de combler ce manque, avec Karl Weierstrass mais aussi Richard Dedekind et Georg Cantor. On peut alors donner des démonstrations rigoureuses de résultats importants d’analyse, comme le théorème des valeurs intermédiaires, ce à quoi s’emploient des élèves de Weierstrass comme Eduard Heine (1821–1881), Georg Cantor (1845–1918), Hermann Hankel (1839–1873) et Hermann Amandus Schwarz (1843–1921). La notion de continuité peut s’énoncer très rigoureusement, comme de nos jours, ce qui permet, par ricochet, d’avoir une définition précise de la discontinuité en un point.

Julius Wilhelm Richard Dedekind (1831–1916).
Gaston Darboux entre en scène
En France, le mathématicien nîmois Gaston Darboux se penche sur ce thème dans une étude publiée en 1875 sous le titre Mémoire sur les fonctions discontinues. Il fait connaître dans notre pays les travaux des mathématiciens allemands. Sa motivation, pourtant, est un peu différente. Il s’intéresse à la continuité de la fonction dérivée. En effet, toute fonction dérivable est continue ; qu’en est-il de la réciproque ? Darboux débute son mémoire en ces termes : « Jusqu’à l’apparition du mémoire de Riemann sur les séries trigonométriques, aucun doute ne s’était élevé sur l’existence de la dérivée des fonctions continues. D’excellents, d’illustres géomètres, au nom desquels il faut compter Ampère, avaient essayé de donner des démonstrations rigoureuses de l’existence de la dérivée […]. La publication du Mémoire de Riemann a décidé la question en sens contraire. »

Jean Gaston Darboux (1842–1917).
Darboux définit ainsi la continuité d’une fonction : « Une fonction f (x) est dite continue, pour la valeur x = x0 , quand on peut prendre h assez petit pour que l’on ait
f (x0 ± θh) − f (x0) < ε en valeur absolue, θ pouvant prendre toutes les valeurs positives plus petites que 1, et ε étant aussi petit que l’on veut. »
Ce qui l’intéresse ensuite est la construction de fonctions certes dérivables mais dont la dérivée n’est pas continue. Il introduit l’exemple désormais classique de la fonction définie sur l’ensemble des nombres réels par f (x) = x 2 sin (1/x) si x est non nul et f (0) = 0. Sa continuité en 0 s’obtient en majorant la valeur absolue de f par x 2, qui tend vers 0 quand x tend vers 0. Cette fonction est dérivable en 0 puisque | f (x) / x | reste inférieur à | x |, qui tend vers 0 en 0. Pour x non nul, on obtient f ’ (x) = 2x sin(1/x) – cos(1/x). Or cette fonction n’admet pas de limite en 0, ce qui montre que la fonction dérivée f ’ n’y est pas continue.
À l’aide de cet exemple (voir article Discontinuités et séries de fonctions, Focus La fonction de Darboux), Darboux construit une fonction dérivable en tout point mais dont la dérivée n’est continue sur aucun intervalle ouvert (c’est-à-dire qu’entre deux points, il existe toujours un point de discontinuité).
En cette fin de XIXe siècle, la notion de continuité, et donc celle de discontinuité, étaient apprivoisées. Le siècle suivant amènera de nouveaux rebondissements dans la modélisation du désordre, avec les fractales chères à Benoît Mandelbrot et la « théorie du chaos » de René Thom.
Lire la suite