Premières curiosités
Les mathématiciens, avant le XIXe siècle, n’étaient guère attirés par ces fonctions d’exception. Leonhard Euler, cependant, toujours très imaginatif, s’était pris à étudier celle définie par
avec plusieurs exposants superposés, qu’il nommait « exponentielle répliquée ». On la retrouve dans son manuscrit De formulis exponentialibus replicatis, avec l’expression
Après des débuts très numériques, où il pose r α = β, puis r β = γ, r γ= δ… et calcule ses valeurs particulières, il poursuit avec des cas de plus en plus compliqués, résolus en passant au logarithme. Il qualifie les résultats obtenus de « phénomènes merveilleux » et échange à leur sujet avec le marquis de Condorcet.

L’exponentielle répliquée d’Euler.
La fonction « partie entière »
L’une des fonctions les plus simples à présenter de nombreuses discontinuités est la fonction partie entière (ou floor function), qui associe à tout réel x le plus grand entier E (x ) inférieur ou égal à x. Ainsi, pour tout x appartenant à l’intervalle [n, n + 1[, E (x ) = n, et E(n ) = n pour tout n entier. Elle est, de par sa définition, continue à droite en tout point d’abscisse entière, mais pas à gauche puisque
Le premier à l’avoir introduite est le mathématicien français Adrien-Marie Legendre (1752–1833), utilisant en 1798 la notation E (x ) pour les besoins de la formule qui va porter son nom, donnant l’exposant
En 1808, le mathématicien allemand Carl Friedrich Gauss (1777–1855) introduit la notation [x] dans la démonstration de son théorème de réciprocité quadratique. On l’écrit parfois aujourd’hui x , comme l’a préconisé en 1962 le Canadien Kenneth Eugene Iverson (1920–2004) pour les langages de programmation.
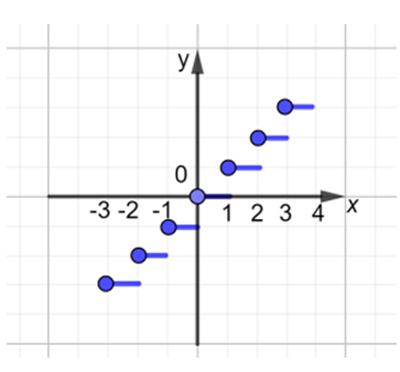
Représentation graphique de la fonction partie entière.
Les fonctions de Dirichlet et pop-corn
La fonction caractéristique d’un ensemble E est l’application
C’est en 1829 que Gustav Lejeune Dirichlet s’intéresse à la fonction qui va porter son nom, la fonction caractéristique de l’ensemble ℚ des nombres rationnels : f (x) = 1 si x est un rationnel, et 0 sinon. Ce sera le premier exemple de fonction discontinue… en tout point !
En effet, si r est un nombre rationnel, alors il existe, dans un de ses voisinages, aussi petit soit-il, un irrationnel x et donc | f (x) – f (r)| = 1 : on ne peut donc pas rendre cette distance aussi petite que l’on veut, comme l’exige la définition de la continuité.
De la même manière, f est discontinue en tout point irrationnel.
Une variante est la fonction popcorn ou fonction des gouttes de pluie. Introduite en 1875 par le mathématicien allemand Carl Johannes Thomae (1840–1921), elle se définit ainsi : tout rationnel x s’écrivant de manière unique p /q avec p et q premiers entre eux, la fonction popcorn vaut alors 1/q pour tout x rationnel, et 0 sinon. Elle a la spécificité, à la différence de la fonction de Dirichlet, d’être discontinue en tout point rationnel, mais continue partout ailleurs !