Le phénomène de Gibbs

Partons d’une scène présentant une forte discontinuité lumineuse, comme celle ci-dessous d’une tasse de café en plein soleil et de son ombre. D’un point de vue pratique, on va manipuler une photo numérisée sous le format JPEG en 300 dpi (c’est-à-dire en trois cents pixels par pouce) de la scène afin de la transformer en un fichier beaucoup plus « léger » de 36 dpi.

La tasse à café en 300 dpi.

La tasse à café en 36 dpi.

Outre le flou introduit par l’opération, on remarque des séries de petits points blancs suivant les lignes séparant les zones claires des zones foncées. Ce phénomène a été découvert en 1848 par le mathématicien britannique Henry Wilbraham (1825–1883) mais porte aujourd’hui le nom du physico-chimiste américain Josiah Willard Gibbs (1839–1903), qui semble le premier à avoir compris son origine mathématique. Il concerne l’accentuation des discontinuités des signaux, que ce soit des signaux électriques, des sons ou des images. Format papier oblige, limitons-nous au cas des images.

Du son à l’image

La compression JPEG est fondée sur la théorie du signal, plus facilement compréhensible avec les sons qu’avec les images. Un son est une vibration de l’air, un phénomène périodique. Il se décompose en une fréquence fondamentale f et des harmoniques, de fréquences n f multiples de la fréquence fondamentale (n est un entier supérieur à 2). Du point de vue mathématique, cela correspond à une somme de sinusoïdes de la forme a_n sin (2π n f t) + b_n cos (2π n f t) où a_n et b_n sont des constantes.

La compression consiste à se contenter des premières harmoniques (n = 2, 3, 4, 5…). L’effet aux points de discontinuité est particulièrement sensible, car le saut de discontinuité s’en trouve nettement augmenté.

En guise d’exemple, considérons la fonction impaire c dite fonction créneau, valant 1 sur l’intervalle ouvert ]0, π[, valant 0 en π et périodique de période 2π. Une fonction h définie sur \( \mathbb{R}\)  est impaire si elle vérifie, pour tout réel x, h (– x) = – h (x).

Ce signal peut être décomposé sous une forme très simple (voir le calcul en encadré) :

\( c(x)=\frac{4}{\pi}\left ( \sin x+\frac{\sin 3x}{3}+ \frac{\sin 5x}{5} +\cdots + \frac{\sin (2n+1)x}{2n+1}+\cdots\right ).\)

Les vagues du gué

Dans la pratique, on ne retient qu’un nombre fini de termes. La surprise vient à ce niveau car la discontinuité en π se trouve accentuée, comme le montre la représentation graphique des quatre premiers termes.

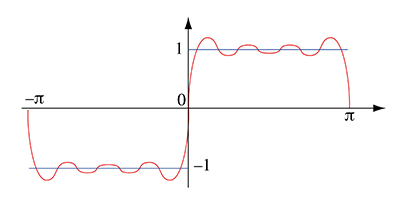
Somme de la série jusqu’à (sin 7x ) / 7.

Augmenter le nombre de termes ne sert à rien, il reste toujours un premier pic qui « monte au-dessus de 1 ». À la limite, ce pic vaut

\( \frac{2}{\pi}\int^\pi_0\frac{\sin x}{x}dx,\)

qui vaut 1,18 à 0,01 près. Le saut de discontinuité de la fonction créneau est donc augmenté de 18 %. D’un point de vue technique, ce résultat se confirme en tout point de discontinuité d’une fonction C¹ par morceaux (voir le dossier « La transformée de Fourier », Tangente SUP 76, 2014). Une fonction h est C¹ par morceaux sur un intervalle [u, v] s’il existe une subdivision u = α₀ < α₁ < … < α_m = v telle que h soit continue et dérivable sur chacun des intervalles ouverts ]α_i , α_i+1[ et que la fonction h ’ admette un prolongement continu sur chacun des intervalles fermés [α_i , α_i+1].

Quand le trop-plein d’un lac, d’un étang ou d’une grosse mare passe sur une route, la discontinuité sur l’un ou l’autre bord de la route crée de petites vagues, ce que l’on peut percevoir sur le bord gauche de la route de la photo. En musique, ceux qui ont une excellente oreille peuvent également entendre le phénomène de Gibbs lors d’un changement de note.

[encadre]

Calcul de la série de Fourier de la fonction créneau

La décomposition de la fonction créneau en série de Fourier est une application du problème consistant à écrire, d’une façon générale, une fonction périodique f , de période 2π, en une somme infinie 

f (x) = a₀ + a₁ cos x + b₁ sin x + a₂ cos2x + b₂ sin 2x + a₃ cos 3x + b₃ sin 3x + …

Le premier terme est facile à calculer, si l’on remarque que toutes les intégrales sur un segment d’amplitude 2π des fonctions de la somme ci-dessus sont nulles. En effectuant les calculs formellement (« comme si la somme était finie »), si l’on peut intégrer f , il reste :

\( \int^\pi_{-\pi}f(x)dx=2\pi a_0.\)

Cette méthode de calcul des coefficients semble s’arrêter là. Mais en fait, on peut obtenir celui de cos x de la même façon, si on multiplie d’abord f (x) par cos x :

f (x) cos x = a₀ cos x + a₁ cos 2x + b₁ cos x sin x + a₂ sin 2x cos x + b₂ cos 2x cos x + …

Ici encore, presque toutes les intégrales sur une période 2π sont nulles, d’où :

\( \int^\pi_{-\pi}f(x)\cos x\, dx=a_1\int^\pi_{-\pi}\cos^2 x\,dx.\)

Pour des raisons de symétrie, on a :

\( \int^\pi_{-\pi}\cos^2 x\,dx=\int^\pi_{-\pi}\sin^2 x\, dx= \frac{1}{2}\pi\int^\pi_{-\pi}(\cos^2 x+\sin ^2 x)dx= \pi.\)

La même démarche permet d’obtenir 

\( a_0=\frac{1}{2\pi}\int^\pi_{-\pi}f(x)dx\)

et, si n ≥ 1,

\( a_n=\frac{1}{\pi}\int^\pi_{-\pi}f(x)\cos (nx)dx\,\, \hbox{et}\,\, b_n=\frac{1}{\pi}\int^\pi_{-\pi}f(x)\sin (nx)dx.\)

On y remarque une dissymétrie dans les coefficients a, souvent résolue en utilisant la formule générale suivante :

\( a_n(f)=\frac{1}{\pi}\int^\pi_{-\pi}f(x)\cos(nx)dx \,\,\hbox{et}\,\, b_n(f)=\frac{1}{\pi}\int^\pi_{-\pi}f(x)\sin(nx)dx,\)

et alors

\( \) \( \) \( f(x)=\frac{a_0(f)}{2}+\sum _{n\geqslant 1}(a_n(f)\cos (nx)+b_n(f)\sin(nx)),\)

cette égalité n’ayant lieu que sous certaines conditions. En particulier, la continuité ne suffit pas pour l’assurer, même si elle suffit pour donner un sens aux coefficients du membre de droite, toujours appelé série de Fourier de f .

La convergence des séries de Fourier vers la fonction qui les génère est un sujet si délicat qu’il est à l’origine de la révolution cantorienne des infinis (voir article L'émergence des fonctions discontinues) ! On ne fait que l’effleurer ici, pour énoncer le théorème de Dirichlet : si une fonction f, de classe C¹ par morceaux, est périodique de période 2π alors sa série de Fourier converge vers la fonction qui la génère en tout point… à condition de remplacer f (x) par la demi-somme entre ses limites à droite et à gauche en x en tout point x de discontinuité.

Dans le cas de la fonction créneau, son caractère impair implique que tous les coefficients a sont nuls. Il reste pour tout entier n. L’intégration est immédiate et conduit à distinguer les cas selon la parité de n. On trouve

\( b_{2n}=0\,\,\hbox{et}\,\, b_{2n+1}=\frac{4}{\pi(2n+1)},\)

d’où finalement :

\( f(x)=\frac{4}{\pi}\sum _{n\geq 0}\frac{\sin[(2n+1)x]}{2n+1}.\)

 [/encadre]