
Au XVIIe siècle, Blaise Pascal a inventé une suite de nombres permettant de calculer le reste d’une division euclidienne, et donc de tester la divisibilité d’un entier par un autre.
Un nombre n étant donné, Pascal considère la suite des restes des puissances de 10 par n en commençant par la puissance 0. Si n = 7, cela donne :

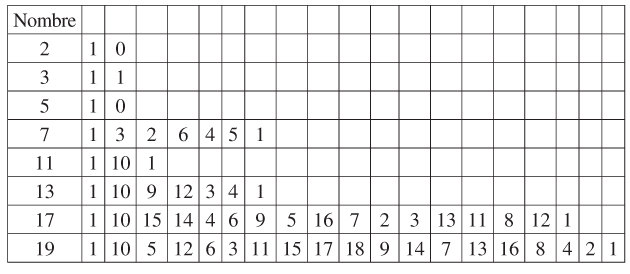
En effet, le reste de 1 est 1 (!), le reste de 10 est 3, celui de 100 est 2… et la suite des restes est périodique. Ce résultat n’est pas lié au nombre 7, il est général. En effet, les restes possibles sont au nombre de n (compris entre 0 et n – 1). Ainsi, parmi les restes des puissances de 0 à n, deux au moins sont égaux, soient les puissances k et k’ (avec k > k’ par exemple). Ceci s’écrit 10 k ≡ 10 k ’ [n], soit encore 10 k – k ’ ≡ 1 [n]. On en déduit que la suite est périodique, et sa période divise k – k ’.
Cette suite est le ruban de Pascal associé à 7.
Calcul du reste d’une division
À partir d’un ruban de Pascal, pour calculer le reste d’un nombre comme 348 dans la division par 7, on écrit les chiffres de 348 dans l’ordre inverse en dessous du début du ruban :

On effectue d’abord, modulo 7, les multiplications en colonnes (1 par 8 donne 8, 3 par 4 conduit à 5, et 2 par 3 produit 6). On additionne alors les résultats obtenus modulo 7 ; on trouve 5, qui est le reste de la division de 348 par 7. L’explication vient des règles de calcul sur les nombres modulo 7. On part de

On trouve rapidement que le reste est égal à 0, donc que 56 218 491 est divisible par 7. Le test de divisibilité par 7 est donc de même nature que le test de divisibilité par 9 : au lieu de faire la somme des chiffres, on en fait une combinaison linéaire dont les coefficients sont ceux du ruban de Pascal. Il en est de même pour tous les nombres.
On peut ainsi facilement déterminer le reste d’un nombre comme 521 365 941 dans la division par 19. On trouve 13, comme le montre le déroulé de la méthode dans le tableau suivant.

L’algorithme se généralise à toute base, et en particulier à la base 2, comme Pascal lui-même l’annonçait (voir le texte de Pascal en encadre).
[encadre]
Le texte de Pascal
Le texte de Pascal est très éclairant sur sa vision, très en avance, de l’arithmétique. Lisez plutôt.
« Rien de plus connu en arithmétique que la proposition d’après laquelle un multiple quelconque de 9 se compose de chiffres dont la somme est elle-même un multiple de 9. […] Dans ce petit traité […], j’exposerai aussi une méthode générale qui permet de reconnaître, à la simple inspection de ses chiffres, si un nombre est divisible par un autre nombre quelconque ; cette méthode ne s’applique pas seulement à notre système décimal de numération (système qui repose sur une convention, d’ailleurs assez malheureuse, et non sur une nécessité naturelle, comme le pense le vulgaire), mais elle s’applique encore sans défaut à tout système de numération ayant pour base tel nombre qu’on voudra, ainsi qu’on le verra dans les pages qui suivent. »
Extrait de De Numeribus Multiplicibus, qui se trouve dans les œuvres complètes de Blaise Pascal (volume 5).

Blaise Pascal (1623–1662).
[/encadre]
Le ruban de « 11 » en base 2 (il s’agit donc du nombre décimal 3) est extrêmement simple :

Donc le reste d’un nombre comme « 1101 » par « 11 » (écriture en base 2) est la somme binaire de ses chiffres, soit 1. À une époque où l’on aime tant opposer sciences et humanités, il est important de rappeler les contributions de Pascal aux mathématiques.
[encadre]
Confectionnez votre ruban
Pour utiliser cette technique, il est bon de disposer d’un certain nombre de rubans. Voici ceux des nombres premiers inférieurs à 20 (on s’est arrêté à la partie périodique) :
[/encadre]
[encadre]
L'algorithme de Vosburgh Lyons
Un autre procédé faisant intervenir un tableau a été établi par le neuropsychiatre et magicien américain Vosburgh Lyons (voir en page www.infinimath.com/tangentemag/saisie/tangentemag/article.php), dit Voz, spécialiste de mentalisme. Sa mise en œuvre peut sembler compliquée, mais le test s’avère efficace surtout pour les grands nombres. Il repose sur les valeurs modulo 7 des puissances de 10. Voyons-en le fonctionnement pour N = 987 654 312.
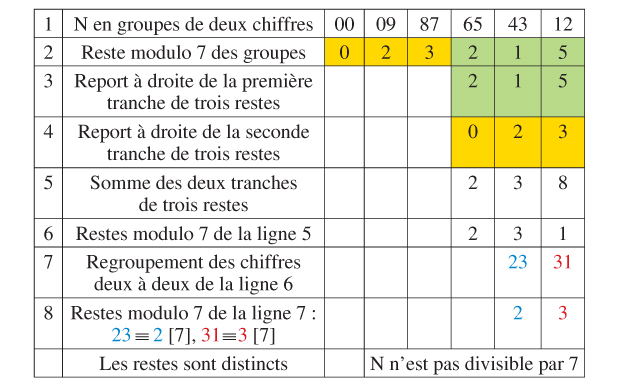
Ligne 1 : on divise N en groupes de deux chiffres (quitte à ajouter des « 0 », on s’arrange pour que le nombre de groupes, ici 6, soit multiple de 3).
Ligne 2 : on remplace chaque case par son reste modulo 7.
Lignes 3 et 4 : on reporte à droite chaque tranche de trois restes.
Lignes 5 et 6 : on en fait la somme et on en écrit le reste modulo 7.
Ligne 7 : on regroupe les chiffres par paires pour former deux nombres de deux chiffres.
Ligne 8 : on écrit le reste modulo 7 de ces deux nombres. S’ils sont distincts, c’est que le nombre initial n’est pas divisible par 7.
Pourquoi ça marche
On remarque que, comme 100 ≡ 1 [7] et 10 ≡ 3 [7], on a 102 ≡ 2 [7], 104 ≡ 4 [7], 106 ≡ 1 [7], 108 ≡ 2 [7], 1010 ≡ 4 [7]…
Si les six groupes de la ligne 1 s’écrivent « abcdef », alors
D’où N ≡ 4a + 2b + c + 4d + 2e + f [7], ou encore N ≡ 4x + 2y + z [7] avec x ≡ (a + d) [7], y ≡ (b + e) [7] et z ≡ (c + f ) [7] sont les restes renseignés en ligne 6.
Les deux nombres r et s de la ligne 8 s’écrivent donc : r ≡ 10 x + y [7] et s ≡ 10 y + z [7].
On en déduit que s – r ≡ –10 x + 9 y + z [7] ≡ 4 x + 2 y + z [7] ≡ N [7].
On voit bien que r = s si, et seulement si, N est divisible par 7.
Le procédé « fonctionne » quel que soit le nombre de chiffres de l’entier N. La divisibilité n’a pas fini de nous étonner !
Élisabeth Busser