
Que ce soit en devinant une carte, un nombre ou en effectuant des opérations stupéfiantes, le magicien utilise chaque fois une astuce mathématique. À vous de jouer en trouvant le truc mathématique qui conduit à la réussite du magicien.

Dominique Souder présentant un tour de cartes basé sur la décomposition en base 2 des entiers.
La carte chercheuse
Le magicien dispose d’un jeu de trente-deux cartes et demande à un spectateur S de battre les cartes, puis de distribuer alternativement carte à carte, faces cachées, le jeu en deux paquets (qui feront donc seize cartes chacun). Le magicien invite S à choisir l’un des deux paquets, à le couper, à regarder et à mémoriser la carte supérieure de l’un de ses deux tas. La carte est laissée à sa place, face cachée, et les deux tas restent en place, séparés. Le magicien coupe maintenant l’autre paquet de seize cartes, et retourne l’une des cartes supérieures de ses deux tas ; on en voit la valeur. Il ramasse alors les quatre tas dans l’ordre suivant (mais sans faire de commentaire sur cette étape) : son tas où se trouve, en haut, sa carte visible V ; puis le tas du spectateur où ne se trouve pas la carte qu’il a choisie ; puis le tas où se trouve sur le dessus (et face cachée) la carte choisie par S ; enfin le dernier tas du magicien. La carte du spectateur se trouve donc être la seizième au-dessus de la carte visible.
Le magicien va maintenant distribuer alternativement, une à une, les cartes en deux tas (elles sont toujours faces cachées, sauf sa carte visible). L’un des paquets distribués contiendra la carte visible : il sera conservé, alors que l’autre paquet, où toutes les cartes sont faces cachées, sera éliminé. En fait, V sert à repérer quel est le tas qu’il faut utiliser, et le magicien déclare que V est une carte chercheuse de celle du spectateur.
Il distribue alternativement, une à une, en deux tas, les seize cartes qui restent. Il conserve le tas de huit cartes contenant V. Il répartit alternativement, une à une, en deux tas, les huit cartes qui restent. Il conserve le tas de quatre cartes contenant V. Il distribue de même les quatre cartes qui restent. Il conserve le tas de deux cartes contenant V, qui est donc allée chercher une dernière carte face cachée : on la retourne, et on vérifie que c’est celle choisie par le spectateur.
Divisibilité par 9
Le magicien tend une calculatrice, un papier et un crayon à un spectateur S. Il lui demande d’écrire les dix chiffres de notre système décimal (0, 1, 2, …9).
Le magicien se retourne pour ne pas voir ce que va faire S maintenant. Le spectateur est invité à écrire trois nombres dont il devra faire la somme ensuite : les deux premiers devront avoir chacun trois chiffres différents pris parmi les dix (chaque chiffre doit être choisi une et une seule fois), le troisième devra être constitué des quatre derniers chiffres (le spectateur peut barrer au fur et à mesure sur sa liste de dix chiffres ceux qu’il a déjà utilisés).
Quand le total T est fait, le magicien demande à S de le multiplier par le code postal de la ville où il habite. Ensuite, S doit écrire sur son papier ce résultat, puis entourer l’un des chiffres, sauf un zéro. Le magicien (qui ne voit toujours rien) demande alors au spectateur de lui énoncer tous les chiffres du résultat, sauf celui qui est entouré, qu’il se charge de retrouver tout seul. Pour corser le défi, il autorise même S à donner les chiffres dans un ordre quelconque.
Répétition de chiffres
Vous demandez à un ami d’écrire sa pointure de chaussure, de multiplier ce nombre par 9, puis de multiplier par votre entier excentrique de seize chiffres, 1 122 334 455 667 789. Votre ami verra alors sa pointure écrite neuf fois en ligne.
Avant de réaliser ce tour, vérifier que vous avez à votre disposition une calculatrice permettant un affichage de dix-huit chiffres (ou un ordinateur ayant un logiciel de calcul à la hauteur).
Digne d’un calculateur prodige !
« Monsieur, vous avez bien un chiffre préféré de 1 à 9 ? Attention, ne me le dites pas, mais pensez-y. Maintenant quel nombre préférez-vous de 3 à 22 ? Cette fois, vous pouvez me dire votre choix.
– Le nombre 12.
Voulez-vous prendre cette calculatrice et faire les multiplications successives que je vais vous indiquer ? Prenez votre chiffre préféré, que je ne connais toujours pas, multipliez-le par 21. Multipliez ce que vous avez obtenu par 143. Multipliez le résultat par 37. Multipliez le tout par 101. Et enfin multipliez encore ce que vous avez obtenu par 9 901. »
Stupéfaction de l’ami, qui fixe sa calculatrice avec des yeux écarquillés.
« C’est curieux ce que vous voyez, n’est-ce pas ? Il y a douze chiffres identiques, et c’est douze fois votre chiffre préféré. Quel miracle ! On peut recommencer si vous voulez avec un autre chiffre préféré et un autre nombre choisi de 3 à 22… »
Le roi du produit
Le magicien a écrit au tableau le nombre 142 857 143. Il a demandé au spectateur de choisir un autre nombre de neuf chiffres, par exemple 123 456 789. Le magicien donne alors le produit de ces deux entiers, en écrivant les chiffres du résultat de gauche à droite.
Décomposition instantanéed’un nombre de six chiffres
Si vous avez l’occasion de passer près de Lyon (Rhône), ne manquez pas d’aller y visiter la Maison des mathématiques et de l’informatique (1 place de l’École). En déambulant parmi les pépites exposées sous la direction du statisticien et médiateur scientifique Jean-Baptiste Aubin, on découvre un jeu d’awalé et ses graines. Une idée de tour émerge.
On prend 3 × 9 = 27 graines, que l’on répartit équitablement dans les trois emplacements de gauche de la rangée supérieure ; chacun de ces trois creux contient donc neuf graines. Tous les autres emplacements (les trois autres creux du haut, les six du bas) sont vides au départ.

La disposition initiale.
Le magicien demande à un spectateur de répartir les graines du premier emplacement dans les creux numéros 1 et 4 (à partir de la gauche) de la rangée inférieure, puis de répartir celles du deuxième emplacement supérieur dans les creux numéros 2 et 5 de la rangée inférieure, et enfin de répartir celles du troisième creux supérieur dans les creux numéros 3 et 6 de la rangée inférieure. Le spectateur est invité à lire le nombre de six chiffres que l’on obtient grâce aux six emplacements maintenant remplis de graines de la rangée inférieure.

Un exemple de disposition des vingt-sept graines proposé
par un spectateur. Le nombre correspondant est 421 578.
Le magicien affirme alors qu’il est capable de décomposer en produit de facteurs premiers le nombre obtenu. Ici, par exemple, il énonce instantanément :
« 421 578 = 37 × 33 × 2 × 211. »
Essayez d’expliquer ces tours arithmétiques avant d’aller voir les solutions en pages suivantes !
Revenons au tour avec la carte chercheuse et essayons de comprendre ce qui a bien pu se passer. Dans le paquet de trente-deux cartes, la carte visible et celle choisie par le spectateur ont été placées dans des positions qui diffèrent de seize numéros. Après la distribution alternative en deux tas, elles ne le seront plus que de huit numéros. Après une nouvelle opération, elles ne le seront plus que de 4. À l’étape d’après, elles ne seront plus séparées que de 2. Et à la distribution finale, la carte visible sera logiquement accompagnée de la carte choisie par le spectateur. C’est finalement grâce à une dichotomie et aux puissances de 2 que réussit ce tour ! Quand on distribue un nombre impair de cartes, on change de tas, mais quand on distribue un nombre pair de cartes, on reste dans le même tas.
Le tour suivant mobilise un critère de divisibilité par 9. On constitue trois nombres avec les dix chiffres. Pour trouver le reste de la division de leur somme par 9, on peut passer par la somme des restes de chacun d’eux par 9. Ce qui est la même chose que la somme des trois sommes des chiffres de leur écriture. On aboutit donc finalement à diviser par 9 la somme des dix chiffres utilisés pour écrire les nombres. Mais
9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 + 0 = 45 = 9 × 5 ; le nombre obtenu alors sur la calculatrice sera toujours divisible par 9. Quand le spectateur entoure un nombre et le cache dans l’énoncé du résultat, le magicien fait la somme des chiffres révélés. Il faut imaginer alors quel est le chiffre manquant pour arriver à un multiple de 9. Par exemple, si le total de tous les chiffres (sauf celui qui est caché) est 37, il manque 8 car le multiple de 9 juste au-dessus de 37 est 45, et 45 – 37 = 8. Si le total est déjà un multiple de 9, le chiffre caché peut être un 0 ou un 9 ; pour que le magicien soit sûr de trouver et de choisir entre les deux possibilités, il a, par précaution, demandé d’entourer un chiffre différent de 0 ; ainsi, la seule réponse possible est 9 dans ce cas.
Avec ou sans la calculatrice
Les tours arithmétiques avec des répétitions de chiffres font souvent intervenir des calculs astucieux ; on en a vu un exemple. Partons du nombre qui s’écrit
1 122 334 455 667 789. Si on le multiplie par 9, on trouve 10 101 010 101 010 101, nombre de dix-sept chiffres qui s’écrit de la gauche vers la droite avec huit fois « 10 », et un 1 à l’extrême droite. Si l’on multiplie un nombre de deux chiffres qui s’écrit AB en base 10 par cet entier, on va trouver un nouveau nombre (de dix-huit chiffres) formé de neuf fois la cellule « AB ». Tout simplement !
Revenons à ce tour étonnant, digne d’un calculateur prodige. Pour le réussir, le magicien doit connaître la décomposition en produit de nombres premiers des « répuns » (ou repunits en anglais), ces entiers s’écrivant uniquement avec des 1 répétés. L’ordre du répun est le nombre de 1 qui interviennent dans son écriture (ainsi, 11 est le répun d’ordre 2). Voici le tableau qu’il convient d’avoir en tête (ou discrètement à portée du regard).
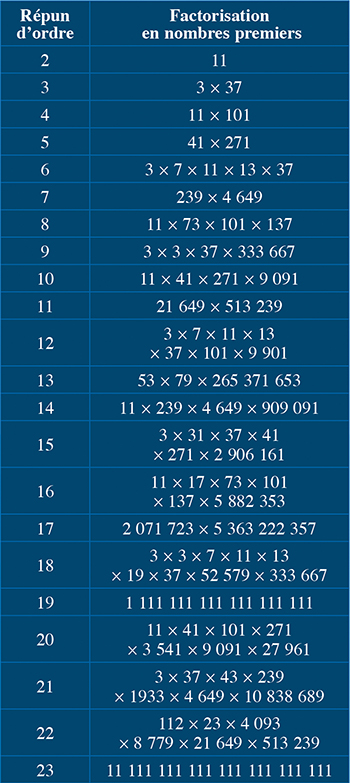
Si, au lieu de multiplier les nombres ci-dessus choisis dans la ligne correspondant au nombre préféré de 3 à 22, vous les multipliez encore par votre chiffre u préféré, le résultat ne sera constitué que d’une répétition de u.
La calculatrice est indispensable, et le magicien doit savoir au préalable combien de chiffres celle-ci peut afficher (jusque 12 pour les calculatrices scientifiques des collégiens, auquel cas le magicien peut proposer le choix d’un nombre de 3 à 12).
Le magicien peut aussi se transformer en « roi du produit ». Si l’on fait la division de
1 000 000 001 par 7, on trouve un quotient exact, qui est 142 857 143. Multiplier tout nombre par ce dernier peut donc se faire en deux étapes : d’abord le multiplier par
1 000 000 001, puis diviser le résultat par 7. Comment multiplier un nombre de neuf chiffres par 1 000 000 001 ? C’est très simple, il suffit de réécrire le nombre une deuxième fois à côté ! Par exemple :
123 456 789 × 1 000 000 001 = 123 456 789 123 456 789.
Il reste donc au magicien à faire de tête une division par 7 d’un nombre de dix-huit chiffres, après avoir imaginé ou visualisé la répétition de l’écriture du nombre de neuf chiffres choisi par le spectateur. On comprend ainsi pourquoi il donne l’écriture du résultat de gauche à droite.
Dans l’exemple : 123 456 789 123 456 789 / 7 = 17 636 684 160 493 827,
et donc 142 857 143 × 123 456 789 = 17 636 684 160 493 827.
Il va vous falloir un peu d’entraînement, c’est sûr, mais d’une part ce tour est très valorisant, et d’autre part il permet de prendre conscience qu’un calcul ne s’exécute pas, il se médite…
Passons maintenant au tour réalisé à partir d’un jeu d’awalé. L’astuce provient de la décomposition instantanée d’un nombre de six chiffres s’écrivant selon la forme particulière abc (9 - a)(9 - b)(9 - c). Les premier et quatrième chiffres sont complémentaires de somme 9, de même que les deuxième et cinquième chiffres, et que les troisième et sixième chiffres. On suppose de plus que c n’est pas égal à 9.
La tactique de répartition des graines permet en effet d’obtenir un nombre M de la forme voulue, en évitant de laisser un creux vide à la position c. Ce nombre M vaut
100 000a + 100 (9 – a) + 10 000b + 10 (9 – b) + 1 000c + (9 – c), soit 999 (100a + 10b + c + 1) après simplification. M est donc un multiple de 999 = 37 × 33.
Le nombre c + 1 n’atteint pas 10, donc il n’a qu’un seul chiffre (au maximum, il vaut 9). L’entier 100a + 10b + c + 1 s’écrit donc avec les trois chiffres ab (c + 1).
Revenons à notre nombre abc (9 – a)(9 – b)(9 – c).
Il est divisible par 37 et par 27, et aussi par celui qui s’écrit ab (c + 1). Ce dernier est un entier de trois chiffres qui doit être assez facile à décomposer de tête en produit de facteurs premiers. Par exemple, 421 578 = 37 × 33 × 2 × 211 a bien la forme voulue (car 4 + 5 = 2 + 7 = 1 + 8 = 9 ; il est divisible par 37, par 27, et par le nombre 421 + 1 = 422). On voit immédiatement que 422 se divise par 2, et comme 211 est premier, on peut même ajouter que 421 578 se divise par 211 et 2, en plus d’être divisible par 37 et 33.
Le magicien commence par annoncer que le nombre est divisible par 37, puis par 3 au moins trois fois (et donc par 27), puis par d’autres entiers. En pratique, il réfléchit à la décomposition du nombre qui s’écrit ab (c + 1) pendant qu’il parle de la division possible par 37, puis par 27 et qu’il confie cette vérification au spectateur qu’il a doté d’une machine à calculer. Mathémagicien, c’est aussi tout un art de la scène !
Lire la suite gratuitement