Connaître les diviseurs... sans diviser

On sait, depuis l’école primaire, reconnaître si un nombre est divisible par 2, 3, 4, 5, 6, 8, 10 ou 11. Pour des diviseurs comme 7, 13, 17, 23, 29… ou même 271, cela semble en revanche relever de la haute voltige. Pourtant, il existe des façons d’y parvenir. Faisons donc le tour, des plus simples aux plus compliqués, des critères de divisibilité dans le royaume des nombres entiers. Or, quand on parle de divisibilité, la notion de congruence (voir encadré) va très souvent faciliter la tâche.

[encadre]

Vous avez dit « congruences » ?

L’existence même du nombre r permet de définir sur l’ensemble ℤ des entiers relatifs une relation d’équivalence : a et a’ sont dits équivalents s’ils ont même reste dans la division par b. On dit encore « a est congru à a’ modulo b », ce que l’on écrit a ≡ a’ [ b ]. On fait ainsi une partition de  \( \mathbb{Z}\)  en b parties disjointes appelées classes, celles des brestes possibles dans la division par b. Chaque classe correspond à une valeur du reste, de 0 à b – 1 ; on les note  \( \{\dot{0}, \dot{1}, \dot{2}%E2%80%A6 \dot{(b-1)} \}.\)  

La relation « est congru à » est compatible avec l’addition, la soustraction, la multiplication et l’élévation à une puissance.

L’application qui à un entier associe sa valeur modulo b est un homomorphisme, c’est-à-dire que le reste d’une somme de deux nombres est congru, modulo b, à la somme de leurs restes ; de même, le reste d’un produit est congru, modulo b, au produit des restes.

On traduit en particulier, en utilisant le vocabulaire des congruences, la notion de divisibilité : « a est divisible par b » équivaut à dire que le reste dans la division de a par b est nul, ce qui s’écrit a ≡ 0 [ b ].

Lorsque b est un nombre premier, de nouvelles propriétés s’ajoutent. Tout élément N non congru à 0 admet un inverse pour la multiplication, c’est-à-dire une famille de nombres (égaux modulo b) qui, multipliés par N, donnent un nombre congru à 1 modulo b. Par exemple, si b = 5, on se convainc aisément que 1 et 4 sont leur propre inverse : 1  \( \times\)  1 ≡ 1 [5], 4  \( \times\)  4 ≡ 16 ≡ 1 [5]. De même, 2 et 3 sont inverses l’un de l’autre : 2  \( \times\)  3 ≡ 6 ≡ 1 [5].

[/encadre]

Révisez vos classiques !

Pour savoir si un entier est divisible par 2 ou 5, les propriétés des congruences ne sont même pas nécessaires. Un nombre N est divisible par 2 si son chiffre des unités u est pair. En effet, en séparant le chiffre des unités u de N, et N, amputé de ce chiffre, que l’on nomme d, alors N = 10 d + u. Comme 10 est un multiple de 2, N est divisible par 2 si, et seulement si, u l’est, c’est-à-dire est pair.

De même pour la divisibilité par 5. Comme 10 est aussi multiple de 5, N est divisible par 5 si, et seulement si, u l’est, c’est-à-dire est égal à 0 ou 5. Avec le vocabulaire des congruences, N ≡ u [2] et N ≡ u [5]. On reconnaît donc la divisibilité de N par 2, ou par 5, à celle de son chiffre des unités.

La technique se généralise à toute puissance de 2 ou de 5 : N est divisible par 2ⁿ ou par 5ⁿ si le nombre formé par ses n derniers chiffres l’est. De même, N est divisible par 10ⁿ s’il est terminé par n zéros.

La divisibilité par 3 ou par 9 se traite en remarquant que pour tout n, 10 ⁿ ≡ 1 [3] et 10 ⁿ ≡ 1 [9]. Ainsi, l’entier N s’écrivant comme la somme de ses chiffres multipliés chacun par une puissance adéquate de 10, N est congru à la somme de ses chiffres, que ce soit modulo 3 ou modulo 9. On en déduit que N est divisible par 3 (respectivement par 9) si, et seulement si, la somme de ses chiffres l’est.

On traite sur le même modèle la divisibilité par 11 : pour tout n pair, 10 ⁿ ≡ 1 [11] et pour tout n impair, 10 ⁿ ≡ –1 [11]. L’entier N est donc divisible par 11 si la différence entre la somme de ses chiffres de rangs impairs et celle de ses chiffres de rangs pairs est multiple de 11.

Un autre résultat important est que si c = ab est le produit de deux nombres a et b premiers entre eux (sans diviseur commun autre que 1), alors un entier N est divisible par c si, et seulement si, il est divisible à la fois par a et par b. Cela permet de reconnaître si un nombre est divisible par 6 (il suffit, comme 2 et 3 sont premiers entre eux, de savoir s’il est divisible par 2 et par 3), par 10, 12 (avec 3 et 4)…

La divisibilité par 7 comme modèle

Et les autres ? De multiples méthodes permettent de tester la divisibilité d’un nombre. Le diviseur 7 est un modèle à partir duquel une généralisation à d’autres nombres peut être imaginée. Évoquons quelques-unes des techniques d’étude de la divisibilité par 7 ; d’autres se trouvent dans l’article le Ruban de Pascal.

Une première méthode, assez courante, que l’on retrouve d’ailleurs pour d’autres diviseurs que 7, consiste à écrire, comme précédemment, N = 10 d + u, en séparant le chiffre des unités u, du nombre (et pas forcément « chiffre ») de dizaines d.

N ≡ 0 [7] équivaut à aN ≡ 0 [7] dès lors que a est premier avec 7. C’est une conséquence du fait que 7 est premier. En effet, N ≡ 0 [7] implique bien sûr aN ≡ 0 [7] ; réciproquement, si aN ≡ 0 [7], il existe b tel que ab ≡ 1 [7], et, en multipliant aN par b, il vient que N ≡ 0 [7].

Ainsi, dire que 7 divise N équivaut à dire que 7 divise par exemple 2N, ou encore que 20d + 2u ≡ 0 [7], c’est-à-dire 21d – d + 2u ≡ 0 [7]. Or 21d ≡ 0 [7], donc « N ≡ 0 [7] » équivaut à « 2u – d multiple de 7 ».

Appliquons ce principe au nombre 357 295. On obtient successivement : 35 729 – 25 = 35 719 ; 3 571 – 29 = 3 553 ; 355 – 23 = 349 ; 34 – 29 = 16, qui n’est visiblement pas divisible par 7. Pour les nombres de peu de chiffres, le critère donne vite la réponse, mais il est très lent sur les grands nombres. Il s’applique cependant à de nombreux autres entiers.

Ainsi, pour 13, N = 10d + u s’écrit, en multipliant par 4, 4N ≡ 40d + 4u [13] ≡ d + 4u [13]. « N ≡ 0 [13] » équivaut à « d + 4u multiple de 13 ».

Il existe, sur le modèles des précédents, des critères de divisibilité plus « exotiques », par 17, 19, 23, 29, 31… 71, 73, 79, 83, 89, 97…Mais qui les utilise ? 

Ainsi, vous établirez sans peine que :

« N ≡ 0 [17] » équivaut à « 5u – d multiple de 17 » ;

« N ≡ 0 [19] » équivaut à « 2u + d multiple de 19 » ;

« N ≡ 0 [23] » équivaut à « 7u + d multiple de 23 » ;

« N ≡ 0 [29] » équivaut à « 3u + d multiple de 29 » ;

etc.

Une seconde méthode est dans le même style. On sépare N en tranches de trois chiffres. On sait en effet que 1 001 est un multiple de 7. Ainsi, pour tout n, 1 000 ²ⁿ ≡ 1 [7] et 1 000 ²ⁿ⁺¹ ≡ –1 [7]. Pour repérer la divisibilité de N par 7, il suffira donc de faire la somme alternée des tranches et voir si le résultat final est divisible par 7. 

On en déduit les curiosités suivantes : tout nombre de six chiffres composé de deux tranches identiques est, du premier coup d’œil, divisible par 7 ; tout nombre de neuf chiffres de trois tranches identiques n’est divisible par 7 que si ces tranches le sont. Enfin, comme 1 001 = 71113, ce critère donne aussi une réponse pour la divisibilité par 11 et par 13.

Un graphe pour s’y retrouver

Outre les méthodes faisant intervenir des « tableaux », que l’on trouvera dans l’article suivant, les critères de divisibilité par 7 semblent avoir beaucoup inspiré les calculateurs, amateurs ou professionnels. Un de ces procédés, utilisant un graphe imaginé par David Wilson, passe par un diagramme qui fournit même le reste de la division par 7 du nombre proposé.

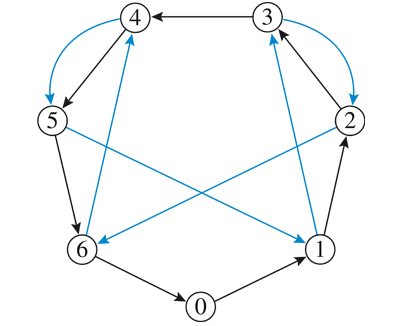
Ce graphe possède sept sommets (ce n’est sans doute pas un hasard !), les nœuds. Certaines flèches sont noires, d’autres sont bleues. Parcourir une flèche noire, c’est ajouter 1 modulo 7 ; parcourir une flèche bleue, c’est multiplier par 10 modulo 7.

Prenons un nombre au hasard, par exemple 978 324. Quel est son reste dans la division par 7 ? Pour l’établir, on part du nœud 0. Le premier chiffre étant 9, on parcourt neuf flèches noires et on se retrouve au nœud 2. Avant de passer au chiffre suivant, on utilise une flèche bleue : on aboutit au nœud 6. Maintenant, au vu du deuxième chiffre, 7, on parcourt sept flèches noires : on se retrouve au nœud 6. À nouveau, on utilise une flèche bleue et on arrive sur le nœud 4. On continue ainsi, de proche en proche, jusqu’à aboutir à 4. Le reste dans la division euclidienne par 7 de 978 324 est bien 4 (vérifiez-le !).

Le graphe original de David Wilson, 
qui lui a donné la forme ludique d’une tête d’animal.

Alors, quel est le « truc » ? Prenons l’exemple du nombre 642, qui peut s’écrire (6 x 10 + 4) 10 + 2. Après les deux premières étapes (les six flèches noires suivies de la flèche bleue), on a 4, résultat modulo 7 de 6 10. L’étape suivante (les quatre flèches noires) donne 1, résultat modulo 7 de 6 10 + 4, et ainsi de suite jusqu’au résultat final… qui est 5, résultat modulo 7 du nombre initial.

Cette méthode peut s’appliquer à la divisibilité par n’importe quel entier, à condition de construire le graphe correspondant. La seule difficulté, peut-être, est la complexité du graphe si le nombre est trop grand…

[encadre]

Six multiples pour le prix d'un

Féru de tours, le « magicien des nombres » Lawrence Vosburgh Lyons (1892–1976), rapporte Martin Gardner, a inventé une façon express de fabriquer de tête six multiples de 7 à six chiffres à partir d’un nombre… non forcément multiple de 7.

Soit un nombre de six chiffres, N = 752 146, non multiple de 7 (son reste est égal à 3). Recopiez-le six fois dans les lignes d’un carré 6  \( \times\)  6, en supprimant successivement l’un des chiffres sur la diagonale à partir de la droite.

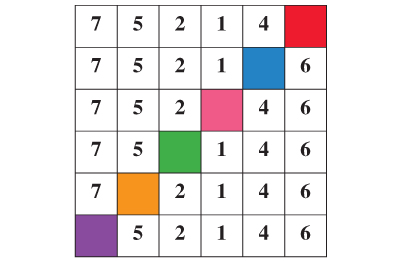
Comme N ≡ 3 [7], sur la ligne 1, pour être multiple de 7, le nombre devra « compenser » cet excès et se terminer par « 43 » : on écrit 3 dans la case rouge (on enlève de 6 le reste 3).

Ligne 2, le nombre devra être tel que « ? 6 » ait même reste que le « 43 » au-dessus de lui, c’est-à-dire 1 : on écrit 3dans la case bleue.

On continue : « ? 4 » ≡ 6 [7], comme « 13 » : on reporte 3 dans la case rose.

On poursuit en ligne 4 : « ? 1 » ≡ 23 ≡ 2 [7] : on inscrit 5 dans la case verte.

Finalement, on note 6 dans la case orange et 5 dans la case mauve.

Voilà : 752 143, 752 136, 752 346, 755 146, 762 146 et 552 146 sont six multiples de 7, obtenus en un « calcul éclair » !

[/encadre]