On Growth and Forms est l’une des œuvres scientifiques les plus originales qui aient été produites au XX e siècle. Son auteur, le biologiste et mathématicien britannique D’Arcy Thompson, y déploie une grande culture classique, mise au service d’un projet intellectuel visant à placer les mathématiques au cœur de l’étude du vivant.
Au moment où il s’attelle à sa tâche, la théorie de l’évolution de Charles Darwin fait encore couler beaucoup d’encre, mais est désormais bien acceptée dans ses principes généraux par la communauté scientifique. Le darwinisme, qui ne s’est pas encore transformé en la théorie synthétique de l’évolution que l’on connaît aujourd’hui, exprime l’idée que les mutations aléatoires qui se produisent chez les individus d’une espèce sont autant d’« essais » involontaires, souvent infructueux ou sans effet mais parfois bénéfiques pour la survie de l’espèce dans son milieu. Sorte d’« optimisation par essais et erreurs », le mécanisme offre une explication des transformations du monde vivant qui se dispense de devoir invoquer une intervention extérieure (notamment divine).
Quantifier l’évolution
Élégante, cette idée de « survie des plus aptes » n’en demeure pas moins surtout qualitative, et ne répond pas à l’évidente question : comment définit-on « les plus aptes » ? Un élément important de réponse est qu’il n’y a pas de définition in abstracto : tout dépend du milieu dans lequel l’espèce évolue, les conditions optimales de survie aux pôles, par exemple, n’étant pas les mêmes que dans une région tempérée.
D’Arcy Thompson tente une autre approche, pour surmonter l’écueil qui consisterait à dire que « les plus aptes » sont simplement… ceux qui survivent. Il cherche dans les mathématiques un critère extérieur de sélection, moins lié au milieu.
Pour une espèce donnée, réaliser un optimum de nature géométrique peut présenter un avantage en soi. Lorsqu’une espèce montre ainsi une forme particulière, l’analyse des propriétés mathématiques de cette forme doit permettre de comprendre quel optimum cette forme réalise, et donc quelle propriété mathématique favorable a été naturellement sélectionnée par l’évolution. En quelque sorte, l’histoire du vivant dans son ensemble serait ainsi celle d’algorithmes d’optimisation d’un genre spécifique, qui n’est pas sans présenter une parenté formelle avec l’algorithme de Monte-Carlo (voir article « La méthode de Monte-Carlo »).
Les algorithmes de la nature
D’Arcy Thompson retrouve ainsi dans la nature diverses manifestations de propriétés d’optimalité, comme par exemple la présence de surfaces minimales chez certains petits animaux aquatiques (à savoir, des surfaces dans l’espace de plus petite aire possible et dont le bord est fixé, comme la caténoïde).
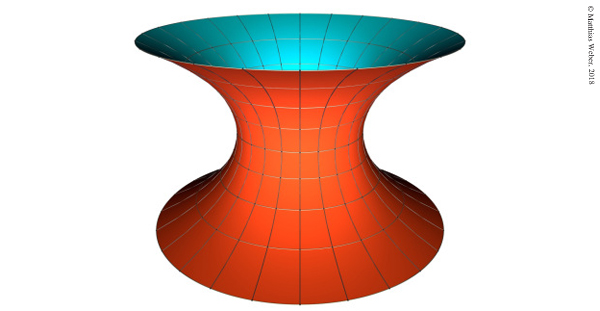
La caténoïde est la surface de plus petite aire
limitée par deux cercles à la verticale l’un de l’autre.
Si, dans certains cas, l’on peut envisager de déterminer mathématiquement une forme ou une taille optimale, parfois l’explication se fait davantage qualitative, tout en reposant sur un argumentaire analytique. Un exemple de tel raisonnement est donné par la taille des organismes monocellulaires.
Dans les premiers temps de la vie sur Terre, les êtres vivants étaient principalement à l’échelle d’une cellule. Une modélisation rudimentaire consiste à représenter celle-ci sous la forme d’une sphère séparant le milieu intérieur du milieu extérieur. Le travail que peut effectuer une cellule pour assurer sa survie est, en première approximation, une fonction de son volume. Si la sphère cellulaire est de rayon r, les capacités productives de la cellule sont donc proportionnelles à r 3 (le volume d’une sphère de rayon r étant égal à (4 / 3) π r 3 ). Quant à sa surface, elle quantifie les possibilités d’échanges avec l’extérieur, soit qu’il s’agisse d’« importer » des matières premières, soit qu’il s’agisse de rejeter les déchets.
La surface de la sphère cellulaire est, elle, proportionnelle à r 2 (la formule exacte est 4 π r 2 ). Le fait que la valeur de r 3 croît plus vite que r 2 à mesure que le rayon augmente implique donc que les capacités productives de la cellule augmentent plus vite que ses facultés d’échanges avec l’extérieur. Doit donc se produire un moment où, pour une cellule, il devient inutile, voire contre-productif, d’être d’une taille dépassant un certain seuil. Il y a ainsi un optimum au rayon d’une cellule, qui équilibre ses capacités d’actions avec les possibilités qui sont les siennes de capter des ressources et d’évacuer ses déchets.
Cet optimum ne peut pas être « calculé précisément » à proprement parler, car il dépend bien entendu beaucoup des propriétés physico-chimiques à l’œuvre. Toutefois, une fois reconnu qu’il existe un optimum mathématique, il devient facile d’expliquer le fait que les cellules n’aient jamais dépassé une certaine taille, évolution aidant.
Ce modèle cellulaire extrêmement rudimentaire suffit donc à offrir une explication très simple au fait que, une fois atteintes leurs tailles optimales respectives, les cellules n’aient pas pu aller plus loin, et que la complexification du vivant soit ensuite passé par des voies nouvelles – en l’occurrence celle des organismes multicellulaires.
Bien d’autres raisonnements sont ainsi présentés par D’Arcy Thompson dans sa vaste synthèse qui remonte jusqu’à de fines considérations faites par Galilée.
En se lançant dans une recherche systématique des propriétés géométriques ou analytiques des formes de la nature, D’Arcy Thompson s’est fait le premier biomathématicien. Reconnu comme un œuvre importante du XX e siècle, On Growth and Forms, qui n’a été traduit en français qu’en 2009 sous le titre Forme et Croissance (Seuil), est cependant toujours demeuré un peu à l’écart des grands mouvements de la science. Cette œuvre, que son auteur lui-même présentait comme une énorme préface, semble devoir à jamais éclairer les marges plutôt que d’être au centre.
[encadre]
D'Arcy Thompson, le premier biomathématicien
De nom complet D’Arcy Wentworth Thompson, cet Écossais parfois considéré comme le premier biomathématicien est né en 1860 et mort en 1948. Pionnier sur le sujet de la conservation des espèces vivantes, il a fait l’essentiel de sa carrière à l’University College de Dundee, puis à l’université de Saint-Andrews à Édimbourg.
Fin lettré et helléniste, il réalisa la première traduction pertinente de l’Histoire des animaux d’Aristote, rendant justice aux connaissances anatomiques des Grecs de l’Antiquité, les traductions antérieures étant considérées comme défectueuses.

D’Arcy Wentworth Thompson (1860–1948) photographié par David Shanks Ewart.
[/encadre]
Lire la suite