La méthode de Monte-Carlo

La complexité de problèmes réels rencontrés en économie, en biologie, en physique, en finance, voire en mathématiques, fait que les méthodes déterministes s’avèrent parfois insuffisantes. Le recours à des méthodes aléatoires numériques utilisant l’informatique se révèle alors d’un secours incroyablement utile. Parmi celles-ci, on retrouve la méthode dite de Monte-Carlo, qui fut mise au point peu avant 1950 par le physicien Nicholas Constantine Metropolis. Elle se montre efficace en mathématiques notamment pour le calcul d’intégrales à dimensions multiples, portant sur de très larges domaines, et fournit en pratique des résultats numériques plus précis que les méthodes classiques déterministes. Voyons en quoi consiste son principe dans un cas élémentaire.

Reproduire artificiellement le hasard

Pour calculer l’intégrale \( \hbox{I}=\int _0^1 f(x)dx\) , on va considérer le réel x (qui varie entre 0 et 1) comme une variable aléatoire pour laquelle il convient de construire une suite de valeurs x₁, x₂… x_n indépendantes, distribuées uniformément sur l’intervalle [0, 1[. On estime alors l’intégrale définie I par la relation suivante (dans laquelle on reconnaît la notion de moyenne) :

\( \hbox{I}-\frac{1}{n}\sum_{i=1}^{n}f(x_i).\)

Les lois faibles des grands nombres (ou le théorème central limite) donnent une idée assez précise de la vitesse de convergence de la méthode, qui est de l’ordre de \( 1/\sqrt{n}\)  et qui est proportionnelle à l’écart type de la variable aléatoire f (x) induite par l’hypothèse de calcul. Dans un cas simple comme celui du calcul de I, cette vitesse de convergence peut paraître faible. Mais elle offre un double avantage. D’une part elle est insensible à la dimension de l’intégrale. D’autre part, elle ne dépend pas de la régularité de la fonction à intégrer, dès que celle-ci est de carré intégrable (hypothèse nécessaire à l’existence de la variance de f (x)).

La véritable difficulté de la méthode consiste alors à bien reproduire artificiellement le hasard. On parle de construction de variables pseudo-aléatoires. Dans le cas simple présenté, l’idée de départ est de simuler une distribution uniforme sur l’intervalle [0, 1] à partir de calculs résolument déterministes, ce qui peut se faire assez aisément.

Les tableurs contiennent par exemple un opérateur fournissant une distribution pseudo-aléatoire qui paraît uniformément distribuée sur l’intervalle [0, 1[ (fonction ALEA()). Cette fonction est une boîte noire qui ne satisfait pas le mathématicien.

Voici un algorithme élémentaire donnant des résultats acceptables et que chacun peut implémenter sur son ordinateur. Considérons les trois entiers (bien choisis) A = 2 051, B₁ = 2 097 153 et C = 4 194 304. On construit les nombres D = A × B₁, puis D / C, dont on prend la partie entière, notée [D / C]. On redéfinit ensuite B₂ = D – [D / C] × C. Le nombre x₁ = B₂ / C est compris entre 0 et 1. On recommence alors la procédure en substituant B₂ à B₁. Les résultats obtenus semblent se distribuer aléatoirement de manière uniforme sur [0, 1[. On peut visualiser la pertinence de ces résultats en considérant le graphique suivant dans le plan, reprenant les mille points obtenus par la suite (x₁, x_1 001), (x₂, x_1 002)… (x_1 000, x_2 000).

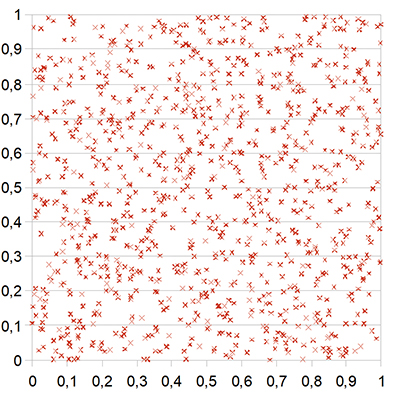
La statistique au service des maths

Dans certains cas concrets d’application, le choix d’une variable aléatoire uniforme n’est pas réaliste et il conviendrait de simuler d’autres types de distributions (voir la Courbe de Gauss : pas si cloche que ça ! dans Tangente 149, 2012). Le théorème central limite conduit souvent à opter pour des distributions normales (les fameuses « gaussiennes »). En effet, tout phénomène qui est la somme d’un grand nombre de « petits » phénomènes aléatoires indépendants de variance finie est distribué normalement. Mais encore une fois, ce choix n’est pas nécessairement judicieux dans tous les cas de figure. Alors ? Comment simuler une distribution quelconque ?

Les mathématiciens George Edward Pelham Box (1919–2013) et Mervin Edgar Muller (1928–2018) ont proposé vers 1958 de simuler toute variable aléatoire à partir de la réciproque de leur fonction de répartition. En effet, pour une variable aléatoire X quelconque, la fonction de répartition F (x) quantifie la probabilité associée à l’ensemble des valeurs pouvant être prises par X et qui sont inférieures ou égales à x :

F (x) = P({ω tels que X (ω) ≤ x}).

F est une fonction croissante dont l’image parcourt l’intervalle [0, 1].

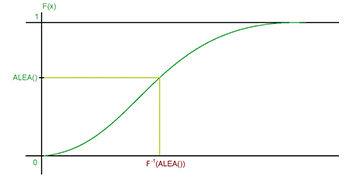
Soit ALEA une variable aléatoire uniformément distribuée sur [0, 1]. Pour une distribution de probabilité de fonction de répartition F, la valeur F^–1(ALEA) simule une valeur numérique compatible avec la distribution envisagée. Graphiquement, les choses sont visualisées sur la figure ci-dessous.

Si théoriquement le problème semble résolu, il n’en demeure pas moins difficile dans certains cas de figure, comme on peut le constater pour la simulation de variables distribuées normalement (voir en encadré).

Dans le cadre de problèmes incluant des variables aléatoires implicites, la méthode est particulièrement efficace. Envisageons en effet l’équation g (x, v₁, v₂… v_k) = 0 dans laquelle v₁, v₂… v_k représentent k variables aléatoires de distribution connue. La variable à étudier, x, devient une variable aléatoire induite par les k précédentes. Toute trajectoire dans l’espace Ω des possibles des k variables v₁, v₂… v_k va induire une valeur particulière de x. La réalisation d’un grand nombre de ces trajectoires et la résolution des équations correspondantes fournit une statistique parfaitement exploitable de la variable x. Le tout avec un niveau d’erreur calculable. Merci aux statistiques !

[encadre]

Simuler la normalité

La fonction densité de probabilité f (x) d’une distribution normale de moyenne m et d’écart type  \( \sigma\)  a la forme suivante :

\( f(x)=\frac{1}{\sqrt {2\pi\sigma}}\exp\Big( -\frac{1}{2}\big( \frac{x-m}{\sigma}\big)^2\Big).\)

En passant à la variable centrée réduite (c’est-à-dire en effectuant le changement de variable   \( z=\frac{x-m}{\sigma}\)  ), on obtient :

\( \int ^1_0 \frac{1}{{\sqrt {2\pi\sigma}}}\exp\Big( -\frac{1}{2}\big( \frac{x-m}{\sigma}\big)^2\Big)dx= \frac{1}{\sqrt {2\pi}}\int ^{1-m/\sigma}_{-m/\sigma} \exp\Big( -\frac{z^2}{2} \Big)dz.\)

En dimension 2 et en coordonnées polaires, un point M du plan de coordonnées (x, y) est déterminé par l’angle θ entre le segment reliant ce point à l’origine et l’horizontale et par la distance r entre le point et l’origine.

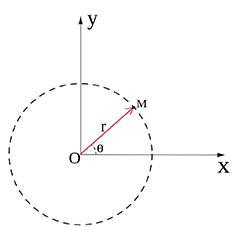
On a x = r cos θ et y = r sin θ avec r un réel positif et θ dans l’intervalle [0, 2π]. En considérant deux variables normales réduites indépendantes x et y, la densité de probabilité à variable bidimensionnelle (x, y) devient le produit des densités associées à chaque variable. Le passage aux coordonnées polaires livre le jacobien suivant :

\( \begin{align*} J=\det \left( \begin{array}{cc} \displaystyle \frac{\partial x}{\partial r}& \displaystyle \frac{\partial y}{\partial r} \\ \noalign{\vskip5pt} \displaystyle \frac{\partial x}{\partial \theta}& \displaystyle \frac{\partial y}{\partial \theta} \end{array} \right) & = \det \left( \begin{array}{cc} \cos\theta & \sin\theta \\ -r\sin\theta & r\cos\theta \end{array} \right) & = r\cos^2\theta + r\sin^2\theta = r. \end{align*}\)  

L’intégrale double de deux variables normales réduites indépendantes x et y se sépare en deux intégrales simples :

\( \frac{1}{2\pi}\int\!\!\!\int \exp\Big( -\frac{1}{2}(x^2+y^2) \Big) dx\, dy= \frac{1}{2\pi}\Big(\int d\theta\Big) \Big(\int r\exp\big( -\frac{r^2}{2} \big)dr\Big).\)

La première quantifie une distribution uniforme de la variable θ sur l’intervalle [0, 2π]. Pour la seconde, on pose r² / 2 = t, ce qui conduit à r dr = dt, pour arriver à une fonction intégrable dont l’image sur l’ensemble des réels positifs est l’intervalle [0, 1]. Ainsi, on est ramené à des distributions uniformes :

\( \int r\exp\Big(-\frac{r^2}{2} \Big)dr= \int \exp(-t)dt.\)

On pose donc θ = 2π × ALEA et  \( \exp\Big(-\frac{r^2}{2} \Big)= \hbox{ALEA} \) , soit  \( r=\sqrt{-2\,\hbox{In(ALEA)}} \)  avec ln le logarithme népérien (fonction réciproque de l’exponentielle exp). La simulation de variables normales réduites se fait finalement au moyen de  \( z=\sin (2\pi\,\hbox{ALEA})\times \sqrt{-2\,\hbox{In(ALEA)}}. \)  .

[/encadre]