Les bons partages

En guise d’apéritif, coupons un saucisson en tranches plus ou moins épaisses. En un coup de couteau dans le saucisson, on obtient deux tranches (particulièrement généreuses, il est vrai). En deux coups de couteau, on obtient trois tranches… et en n coups de couteau, on obtient n + 1 tranches. Aucune surprise jusque-là : on se doute bien qu’on tient là le moyen d’obtenir le plus grand nombre de tranches possibles en n coups de couteau car, à moins d’avoir abusé des boissons disponibles sur la table, personne ne s’amusera à couper deux fois exactement au même endroit. Pourtant, cette question de charcuterie est le point de départ d’interrogations moins triviales.

Qui veut une part de pizza ?

Vous vous souvenez peut-être qu’un célèbre gaulois légèrement enrobé à qui l’on avait demandé de couper trois parts d’un gâteau entamé destiné à Cléopâtre y est parvenu en deux coups de couteau seulement. Fixons un peu mieux les choses et considérons le partage d’une pizza, ou d’un disque, en n coups de couteau, c’est-à-dire par n droites.

En un coup de couteau dans le disque, on obtient deux parts. En deux coups de couteau, on en obtient quatre. Et en trois coups de couteau ?

La version classique des repas de famille ou des soirées entre amis donne six parts, mais combien de parts peut-on obtenir au maximum ? Il n’est pas du tout demandé que ces parts soient équitables (c’est un autre problème, tout aussi riche, mais dans les faits il y a toujours des convives plus gourmands que d’autres).

Pour atteindre ce maximum, l’idéal serait que le troisième coup de couteau coupe les deux premiers. À cela, rien d’impossible, et l’on obtient ainsi un découpage qui produit sept parts. Cette situation est suffisamment connue pour que la langue anglaise lui donne un nom, le lazy caterer’s problem (littéralement le « problème du traiteur paresseux »).

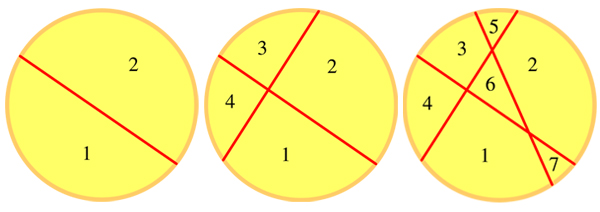
De gauche à droite : Partage de la pizza en un coup de couteau
puis en deux coups de couteau et en trois coups de couteau.

Évidemment, on ne va pas s’arrêter là. Combien de parts peut-on obtenir au maximum en n coups de couteau ? L’idée est la même : l’idéal est de couper un maximum de régions à chaque nouveau coup de couteau, et donc de faire en sorte que chaque nouveau coup de couteau coupe les précédents.

Cette configuration est toujours réalisable ; il suffit que les droites tracées soient toutes sécantes deux à deux, et que jamais trois droites ne soient concourantes. Pour y parvenir, placez la lame de votre couteau en un point qui n’est pas déjà une intersection de deux coupes, puis faites varier l’angle de coupe : vous pourrez toujours faire en sorte d’éviter les autres intersections tout en traçant une nouvelle droite non parallèle aux précédentes. En effet, un nombre fini d’angles sont interdits, mais les choix d’angles possibles sont infinis. Et si jamais les intersections des droites ne tombent pas toute à l’intérieur du disque, il suffit de réduire la figure jusqu’à ce que ce soit le cas.

Le retour du saucisson

Appelons piz(n) le nombre maximum de parts obtenues en n coups de couteau. Peut-on exprimer piz(n) en fonction de n ? C’est là que le saucisson fait son retour.

Considérons n droites formant un maximum de régions possibles, puis traçons-en une autre de façon à produire à nouveau un maximum de régions. Cette dernière droite doit donc couper toutes les précédentes. Or on a vu à l’apéritif que si une droite est coupée en n points, elle se retrouve découpée en n + 1 morceaux. Chacun de ces morceaux coupe une des régions précédentes en deux et on se retrouve finalement avec piz(n) + n + 1 morceaux de pizza.

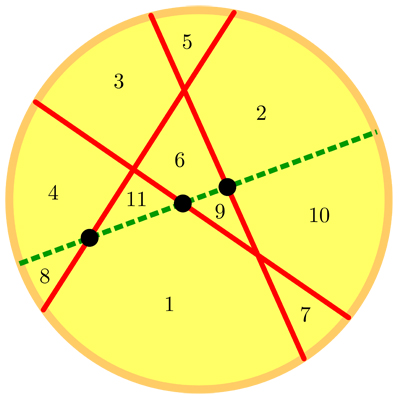
La nouvelle coupe (en vert basilic) coupe les trois précédentes (en rouge tomate) 
en trois points (en noir olive), créant ainsi quatre nouvelles parts
(numérotées 8, 9, 10 et 11).

On a donc piz(n + 1) = piz(n) + n + 1, et ainsi, de proche en proche :

piz(n) = piz(0) + 1 + 2 + 3 + 4 +… + n.

Puisque piz(0) = 1, on trouve finalement que piz(n) est la somme des n premiers entiers naturels non nuls, plus 1. 

Ainsi, 

  \( \text{piz}(n) = 1 + \dfrac{n(n+1)}{2} = \dfrac{n^2 +n +2}{2}.\)

Une part de pastèque

Avec une pastèque, l’idée est de réfléchir en trois dimensions et d’obtenir un maximum de régions en divisant l’espace par des plans. Là aussi, les premiers cas sont assez simples à concevoir. Avec un plan, on obtient deux régions. Avec deux plans on en trouve quatre et avec trois plans, on en obtient huit.

Partage de l’espace (ou d’une pastèque) en deux morceaux par un plan.

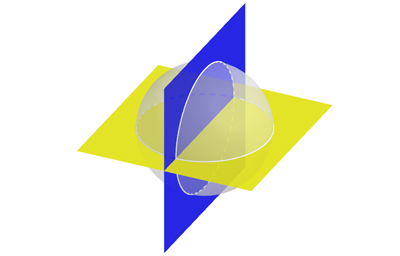
Partage de l’espace (ou d’une pastèque) en quatre morceaux par deux plans.

Avec quatre plans, les choses sont un peu plus délicates à se représenter, mais en étant soigneux on peut compter quinze régions.

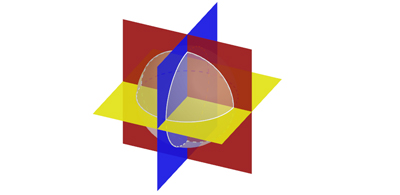
Partage de l’espace (ou d’une pastèque) en huit morceaux par trois plans.

Un raisonnement voisin de celui mené pour les pizzas montre qu’il existe bien un nombre maximum de régions, que l’on trouve en divisant l’espace à l’aide de n plans. Ce nombre cak(n) est obtenu en disposant les plans de sorte qu’ils soient tous sécants deux à deux et que les droites d’intersection ne soient pas communes à plus de deux plans.

Partage de l’espace en quinze morceaux par quatre plans : le morceau central est un tétraèdre et on peut associer un autre morceau à chacune des six arêtes, chacune des quatre faces et chacun des quatre sommets.

Imaginons disposer déjà d’une situation pour laquelle l’espace est divisé en un maximum de régions par n plans. Pour obtenir cak(n+1) régions à l’aide d’un nouveau plan, il faut que celui-ci coupe tous les autres. Les droites d’intersection des n premiers plans avec le nouveau forment une situation bien connue : celle de la pizza ! Ces droites délimitent n régions planes dans le nouveau plan de coupe, et chacune de ces régions vient couper en deux une région de l’espace. Ainsi, on vient d’établir que cak(n+1) = cak(n) + piz(n).

De proche en proche, on obtient alors :

cak(n) = cak(0) + piz(0) + piz(1) + piz(2) +… + piz(n).

Un peu d’algèbre donne finalement :

  \( \text{cak}(n) = \dfrac{n^3 +5n +6}{6}.\)

Cela établit au passage que l’entier n³ + 5n est toujours divisible par 6.

[encadre]

Avec les coefficients binomiaux

Le coefficient binomial 

\( \begin{pmatrix} n \\ k \end{pmatrix} = \dfrac{n!}{k!(n-k)!}\)

est le nombre de parties à k éléments prises dans un ensemble à n éléments. On le note aussi  \( \text{C}^k_n.\)

Le nombre sauc(n) de tranches de saucisson obtenues après n coupes est n + 1, ce que l’on peut écrire 

\( \text{sauc} (n) = \begin{pmatrix} n \\ 0 \end{pmatrix} + \begin{pmatrix} n \\ 1 \end{pmatrix}.\)

Pour les pizzas, on a 

\( \text{piz}(n) = \dfrac{n^2 +n+2}{2}\)

et on peut établir que

\( \text{piz}(n) = \begin{pmatrix} n \\ 0 \end{pmatrix} + \begin{pmatrix} n \\ 1 \end{pmatrix} + \begin{pmatrix} n \\ 2 \end{pmatrix}.\)

Pour les gâteaux et autres pastèques, on obtient 

\( \text{cak}(n) = \begin{pmatrix} n \\ 0 \end{pmatrix} + \begin{pmatrix} n \\ 1 \end{pmatrix} + \begin{pmatrix} n \\ 2 \end{pmatrix} + \begin{pmatrix} n \\ 3 \end{pmatrix}.\)

En fait, toutes ces formules se généralisent. Le nombre maximal de régions obtenues en divisant un espace à ddimensions avec nhyperplans (espaces vectoriels de dimension d – 1) est donné par

\( \begin{pmatrix} n \\ 0 \end{pmatrix} + \begin{pmatrix} n \\ 1 \end{pmatrix} + \begin{pmatrix} n \\ 2 \end{pmatrix} + \begin{pmatrix} n \\ 3 \end{pmatrix} +\ldots + \begin{pmatrix} n \\ d \end{pmatrix}. \)

Références :
- Mathématiques discrètes et combinatoire. Bibliothèque Tangente 39, 2010.
- Vecteurs et espaces vectoriels. Bibliothèque Tangente 65, 2018.

[/encadre]

Un petit donut avant de partir ?

On pouvait s’y attendre, ces questions de découpage optimal (en termes de nombre de morceaux) s’accommodent à toutes les saveurs. Si le melon et le gigot d’agneau désossé sont finalement semblables de ce point de vue, il en va tout autrement pour les donuts au chocolat ou les beignets de calamars frits, ce qui correspond en mathématique à une forme de tore. Dans ce cas, le raisonnement est un peu plus subtil mais le résultat final s’exprime lui aussi par une expression polynomiale de degré 3 : le nombre maximal de morceaux que l’on puisse obtenir après n coupes planes est cette fois

  \( \text{don}(n) = \dfrac{n^3 +3n^2 +8n}{6}.\)

Là encore, la formule établit au passage que l’entier n ³ + 3n ² + 8n est toujours divisible par 6.

Tiens, il reste un bretzel, ça vous dit de remettre le couvert ?

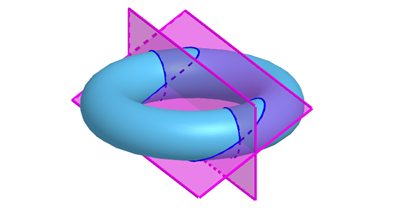
Un beignet coupé en six morceaux en deux coupes.

[encadre]

Le problème des cordes

Un problème célèbre et assez voisin de celui des pizzas est attribué au mathématicien canadien Leo Moser (1921–1970). Disposez n points sur un cercle et tracez toutes les cordes possibles ; combien de régions peut-on former au maximum ? Pour les premières valeurs de n, on trouve 1, 2, 4, 8, 16… mais la suivante n’est pas 32.

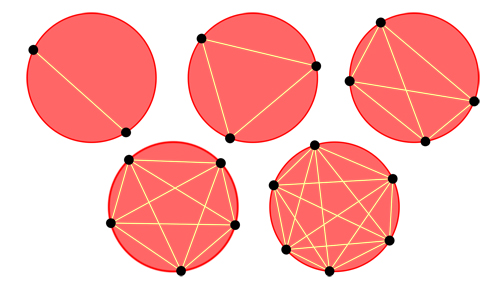
Partage d’une pizza par des cordes. On obtient deux, quatre, huit, seize et… trente et une parts.

En fait, la réponse est donnée par la formule  \( 1+ \begin{pmatrix} n \\ 2 \end{pmatrix} + \begin{pmatrix} n \\ 4 \end{pmatrix}. \)

La même formule fournit le nombre maximum de régions délimitées par n hyperplans dans un espace à quatre dimensions.

En revanche, l’expression du nombre minimum de régions que l’on peut obtenir en reliant n points sur un cercle est nettement moins sympathique. Les lecteurs intéressés pourront consulter à profit l’Encyclopédie en ligne des suites de nombres entiers (OEIS) de Neil Sloane (sur le site www.oeis.org il s’agit de la suite A006533).

Références :

- Pliages, découpages et magie. Gianni Sarcone et Marie-Jo Waeber, POLE, 2012.

- Découpages et pavages. Bibliothèque Tangente 64, 2018.

[/encadre]