Les triangles de Heilbronn

Le mathématicien germano-canadien Hans Arnold Heilbronn (1908–1975) était un spécialiste de théorie des nombres. La conjecture qui porte son nom appartient à la géométrie discrète : le problème des triangles de Heilbronn consiste à placer N points sur un ensemble prédéterminé de sorte que la plus petite aire des triangles qu’ils forment soit la plus grande possible. 

L’optimisation porte ainsi sur les  \( \dfrac{\text{N(N-1)(N-2)}}{6}\)  triangles dont les sommets sont trois des N points (avec N ≥ 3).

Le problème original a été posé dans le carré unité (d’aire 1), les points pouvant être placés n’importe où à l’intérieur ou sur le bord. L’aire optimale à trouver est appelée nombre de Heilbronn, et notée H(N). Par la suite, le problème a été étendu à toutes sortes de figures.

Aucune solution générale n’est connue au problème de Heilbronn : l’emplacement optimal des points et l’aire optimale ne sont connus que pour quelques valeurs de N. La recherche porte aujourd’hui sur les estimations et sur les méthodes d’approximation.

Le cas du carré

Au début pourtant, tout va bien. Il est par exemple facile de montrer que H(3) = 1/2 = 0,5. Lorsqu’on ajoute un quatrième point, cela ne diminue pas le nombre de Heilbronn : H(4) = 1/2 = 0,5.

À gauche H(3) = 1/2. À droite H(4) = 1/2.

Pour poursuivre l’exploration, il va falloir un peu plus d’outils. On choisit pour commencer de se placer dans le repère orthonormé dont l’origine est le sommet du carré qui se trouve en bas à gauche.

Lorsque N vaut 5, l’un des points doit se situer sur un sommet, et chacun des quatre autres doit être placé sur un côté différent du carré. On considère alors les points A(0, 0), B(b, 0), C(0, c), D(1, d ) et E(e, 1). Sans perte de généralité, on peut supposer d ≤ c, e ≤ b et
1 – d ≤ b (des symétries orthogonales permettent toujours de se ramener à ces cas).

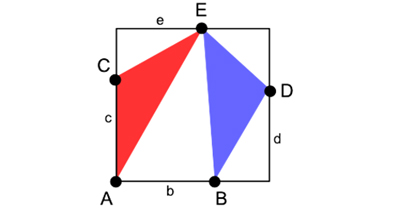
Configuration optimale dans le cas N = 5.

On calcule ensuite l’aire des  \( \dfrac{5(5-1)(5-2)}{6} = 10\) triangles impliqués dans le schéma. C’est très simple lorsque A est l’un des sommets. Pour les autres triangles, on le fait en soustrayant deux triangles rectangles d’un trapèze. Il vient finalement que quatre triangles peuvent être les plus petits : ABD (d’aire bd /2), ACE (d’aire ce / 2),
BDE (d’aire 1 / 2 – de / 2 – b (1– d ) / 2) et CDE (d’aire 1 / 2 – de / 2 – c (1– e) / 2). L’optimum est atteint lorsque c = b et e = d, c’est-à-dire lorsque la figure est symétrique par rapport à la diagonale issue de A. Il reste à égaliser les aires rouge et bleue, ce qui donne bd / 2 = 1 / 2 – d ²/ 2 – b (1– d ) / 2, soit b = 1 – d ². Entre 0 et 1, le maximum de la fonction (1 – d ²) d / 2 est atteint lorsque 1 – 3d ² = 0, c’est-à-dire lorsque  \( d= \dfrac{1}{\sqrt{3}}.\)

On a donc finalement obtenu : 

\( \text{H} (5) = \dfrac{\sqrt{3}}{9} = 0,192450 \ldots\)  

Lorsque N vaut 6, Andreas Dress, Lu Yang, Jingzhong Zhang et Zhenbing Zeng ont démontré en 1995 que l’emplacement optimal des points est obtenu par la transformation affine d’un hexagone régulier. Considérons les points
A(a, 0), B(b, 0), C(0, 1/2), D(1, 1/2), E(a, 1) et F(b, 1).
Sans perte de généralité, on choisit a ≤ 1 – b. Les triangles les plus petits sont isométriques au triangle ABD (rouge) ou au triangle ACE (bleu). L’égalité des aires donne (b – a) /4 = a /2, soit b = 3a. Avec a ≤ 1 – b, il vient donc a ≤ 1/4. Ainsi, H(6) = 1/8 = 0,125.

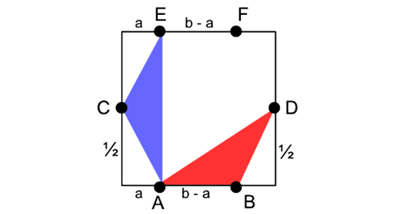
Configuration optimale dans le cas N = 6.

Lorsque N vaut 7, Zhenbing Zeng et Liangyu Chen ont démontré en 2008 que, pour la première fois, des points doivent être placés strictement à l’intérieur du carré. La figure qui suit illustre les huit triangles les plus petits. On trouve H(7) = 0,083859…

Configuration optimale dans le cas N = 7. 
Des points se trouvent à l’intérieur du carré. 

Cette solution correspond à la deuxième racine de 152 x ³ + 12 x ² – 14 x + 1 = 0. Ce polynôme ne tombe pas du ciel : afin de le faire apparaître, on procède en trois étapes. Déjà, on classe les configurations des points à tester en fonction de leur nature combinatoire et de leur répartition dans le carré. Le problème initial revient à analyser deux cent vingt-six configurations. Chacune d’elles alimente un problème de programmation non linéaire. Ensuite, on simplifie chacun de ces problèmes en recherchant les contraintes lâches dans le domaine du possible. Enfin, on atteint les limites, et on montre qu’un seul cas permet d’obtenir l’optimisation, à une isométrie près. N = 7 est également la dernière valeur pour laquelle l’emplacement optimal des points a été trouvé et l’aire optimale a été calculée. Pour les valeurs suivantes, seules des bornes inférieures sont proposées ; les nombres de Heilbronn pourraient être plus grands que ces estimations.

Par exemple, lorsque N vaut 8, le record est détenu par Francesc Comellas et José Luis Andres Yebra depuis 2001. On considère les points
A(0, 0), B(b, 0), C(2(1 – b), c), D(1, c), E(0, 1 – c), F(2b – 1, 1 – c), G(1 – b, 1) et H (1, 1).
Les triangles les plus petits sont isométriques au triangle ACD (rouge), BDH (bleu) ou BCE (jaune). L’égalité des trois aires donne (2 b – 1)c / 2 = (1 – b)(1 – c) / 2 = 3b / 2 – 1 – c (2 b – 1), soit c = (1 – b) / b = (3b – 2)/(3(2b – 1)). L’équation du second degré donne

\( b=(11+\sqrt{13}) / 18\)

puis

\( c=(5-\sqrt{13}) / 6.\)

On trouve alors

\( \text{H}(8) \ge (\sqrt{13}-1)/36 = 0,072376 \ldots\)

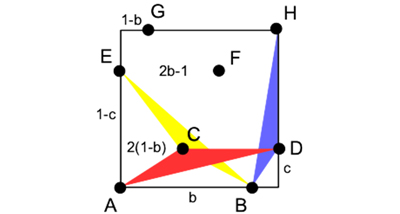
La configuration obtenue par Francesc Comellas et Luis Yebra
dans le cas N = 8.

Le triangle équilatéral

Passons maintenant du carré au triangle équilatéral d’aire 1 (son côté est c = 2 . 3 ^–1/4) et appelons T(N) l’aire recherchée. Déjà, T(3) = 1. Ensuite, en introduisant G le centre de gravité du triangle équilatéral, T(4) = 1/3.

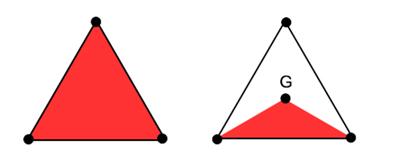
À gauche T(3) = 1. À droite T(4) = 1/3.

Lorsque N est égal à 5, Royce Peng a trouvé l’emplacement optimal des points en 1989. On obtient les points I, J et K tels que :

 - I est le symétrique du sommet du triangle équilatéral par rapport à [JK] ;

 - le côté du triangle équilatéral IJK vaut c / k.

Les triangles les plus petits sont ainsi isométriques aux triangles rouge, bleu et jaune. L’égalité des aires donne (k – 2) / k = 1 / k ², soit

\( k=1+\sqrt{2}.\)

Cela conduit à 

\( \text{T}(5) = 3 - 2 \sqrt{2} = 0,171572\ldots\)

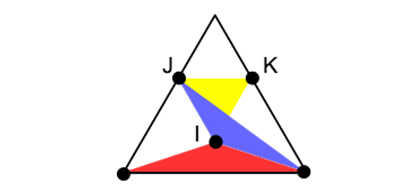
Configuration optimale pour N = 5.

Lorsque N vaut 6, Lu Yang, Jingzhong Zhang et Zhenbing Zeng ont obtenu l’emplacement optimal des points en 1991. Sur la figure suivante, en raisonnant avec les aires résultant du découpage du grand triangle, on détermine les positions des points sur les côtés.

On obtient les points M(c / 4, 0), N(3c / 4, 0),

\( \text{P} (c / 8, c \sqrt{3}/16),\)

\( \text{Q} (7c / 8, c \sqrt{3}/16),\)  
et

\( \text{R} (1 / 2, c \sqrt{3}/4).\)

On notera la coïncidence T(6) = H(6) = 1/8.

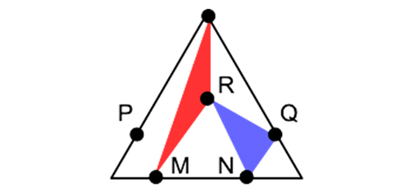
Configuration optimale pour N = 6.

L’emplacement optimal des points n’a été trouvé et l’aire optimale n’a été calculée que pour les six premières valeurs de N. Ensuite, comme pour le cas du carré unité, seules des bornes inférieures ont été proposées.

L’erreur de Heilbronn

Après le carré et le triangle, passons au disque ! Appelons D(N) l’aire recherchée dans le disque d’aire 1 ; son rayon est \( 1/\sqrt{\pi}.\)

Lorsque N varie de 3 à 7, l’emplacement optimal des points est aux sommets du polygone régulier correspondant et l’aire optimale est celle d’un triangle dont les sommets sont trois sommets consécutifs de ce polygone. Cela donne la formule D(p) = (2 / π) sin(2π / p) sin²(π / p), où p est le nombre de points. On trouve ainsi :

\( \text{D}(3) = 3\sqrt{3} /4\pi = 0,413496\ldots ;\)

D(4) = 1/π = 0,318309… ;

\( \text{D}(5) = \sqrt{50 -10 \sqrt{5}}/ 8\pi = 0,209181\ldots ;\)

\( \text{D}(6) = \sqrt{3} /4\pi = 0,137832\ldots ;\)

D(7) = (2/π) sin(2π/7) sin²(π/7) = 0,093700…

Lorsque N = 8, curieusement, David Cantrell a démontré en 2006 que, pour la première fois, un point doit être placé à l’intérieur du disque. La formule précédente donnerait 0,065924… Mais on peut faire mieux en conservant les points précédents et en ajoutant le centre du cercle. L’aire optimale est cette fois celle d’un triangle dont les sommets sont le centre du cercle et deux sommets séparés par deux ou trois sommets de l’heptagone. On calcule que D(8) = sin(π / 7) / 2π = 0,069054…

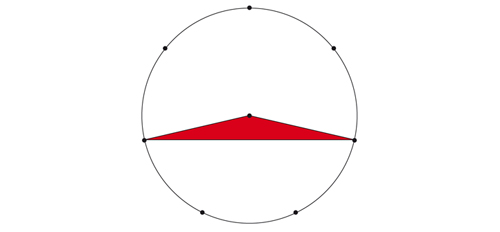
Ensuite, là encore, seules des bornes inférieures sont connues.

Revenons au carré. Heilbronn avait conjecturé vers 1950 que, lorsque N est « très grand », H(N) est minoré asymptotiquement par 1 / N², à un facteur constant près. Mais il s’était trompé.

Le mathématicien hongrois Paul Erdös a d’abord observé que l’on ne peut pas trouver de borne plus petite, toujours à un facteur constant près. En effet, si N est un nombre premier, trois des N points situés aux emplacements (i, i ² modulo N) dans une grille N N ne sont jamais alignés. En appliquant la formule de Pick (voir FOCUS), chaque triangle a une aire au moins égale à 1/2. Puis on modifie l’échelle afin de ramener la grille au carré d’aire 1. Le nouvel ensemble de points est tel que l’aire la plus petite est au moins proportionnelle à 1 / N². Enfin, si N n’est pas un nombre premier, on reprend le même raisonnement avec le plus petit nombre premier qui lui est supérieur.

Les Hongrois Janos Komlos, Janos Pintz et Endre Szemeredi ont ensuite démontré, en 1981, que la minoration est en (log N) / N². Plus précisément, ils ont démontré que, lorsque N est suffisamment grand,

c (logN) / N ² ≤ H(N) ≤ C / N ^{8 / 7 – ε}, où c et C sont des constantes et où 0 < ε < 1.

De nouveaux axes de recherche

L’encadrement précédent étant encore « très large », de nouvelles idées sont exploitées, mais sans succès significatif pour le moment. On cherche notamment à analyser le comportement d’ensembles de points distribués « au hasard ». Tao Jiang, Ming Li et Paul Vitanyi ont démontré en 2001 que les deux bornes de l’encadrement sont alors en 1/ N³, ce qui a l’immense mérite d’homogénéiser leurs puissances. La démonstration utilise la complexité de Kolmogorov, qui permet de définir la taille du plus petit algorithme (dans un langage de programmation donné) qui produit l’emplacement optimal des points.

Plus généralement, le problème a été saisi par les informaticiens, car il s’applique à des sujets de recherche opérationnelle. L’emplacement optimal des points étant donné, quelle que soit la triangulation de la surface, on garantit que l’aire de chaque triangle ne sera pas inférieure au seuil calculé.

La recherche est donc loin d’être terminée et, même sans programmer, le lecteur passionné pourra espérer battre de nouveaux records dans les situations où l’optimisation n’est pas certaine.

[encadre]

Le théorème de Pick

Georg Alexander Pick (1859–1942) a découvert une façon étonnante de calculer l’aire de certains polygones, ceux dont les sommets sont sur un maillage orthogonal régulier (constitué des points à coordonnées entières d’un repère orthonormé). Pour mesurer leur aire, Pick compte le nombre i de points du maillage à l’intérieur du polygone ainsi que le nombre b des points du maillage sur le bord du polygone, 10 et 6 dans le cas de la figure. L’aire A est égale à i + b / 2 – 1, ce qui fait 12 ici. Vérifiez-le !

Pour démontrer la formule de façon générale, on peut commencer par le cas des triangles dont les sommets sont des points du maillage, puis montrer que tout polygone s’obtient en partant d’un triangle de ce type et en en ajoutant progressivement.

H.L.

Références :

Mathématiques discrètes et combinatoire.Bibliothèque Tangente 39, 2010.

Découpages et pavages. Bibliothèque Tangente 64, 2018.

[/encadre]