Les abeilles économes

 Un gâteau de cire et ses alvéoles hexagonales.

Ce que l’on appelle parfois le « gâteau de miel » des abeilles est en réalité un « gâteau de cire », que construisent ces insectes pour y entreposer leur miel. Vu du dessus, il montre ses alvéoles, en forme d’hexagones juxtaposés. Vu de profil, il fait voir que ces hexagones sont en fait les sections droites de prismes hexagonaux accolés. Vu « par le fond », il offre à un œil averti un ensemble de trois losanges, assemblés comme au sommet d’un rhomboèdre. Dans cette structure se cachent, comme le dit Emile Fourrey en 1907 dans ses Curiosités géométriques (« Applications diverses », chapitre III), « deux intéressants problèmes de minimum ».

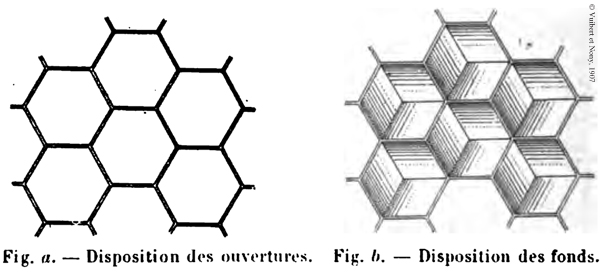
Comment Emile Fourrey voit les alvéoles.

Un problème de fond

Dans le processus de construction, tout se passe comme si le mot d’ordre était d’économiser la cire. Pour le corps des alvéoles, tout d’abord : opter pour une section droite en forme d’hexagone n’est pas anodin, car de tous les polygones pavant le plan, c’est celui qui, à aire donnée, possède le plus petit périmètre. En effet, à cause de leurs angles aux sommets, les seuls polygones réguliers permettant de couvrir le plan sans trous ni chevauchements sont le triangle équilatéral, le carré et l’hexagone régulier. En plus, parmi ces trois sortes de polygones réguliers, celui qui, pour une même aire A, a le plus petit périmètre, est précisément l’hexagone régulier. C’est donc celui-ci qui consomme le moins de cire pour les parois : première économie.

La construction des fonds des alvéoles permet une autre économie : non seulement adosser les cellules permet d’utiliser un même fond deux fois, mais en plus le choix de la forme rhomboédrale optimise l’aire totale de l’alvéole pour une cellule de section et de hauteur données.

Les alvéoles dans l’espace selon Emile Fourrey.

Voici, en respectant les notations du dessin précédent, une alvéole posée sur sa face ouverte UVXYZT.

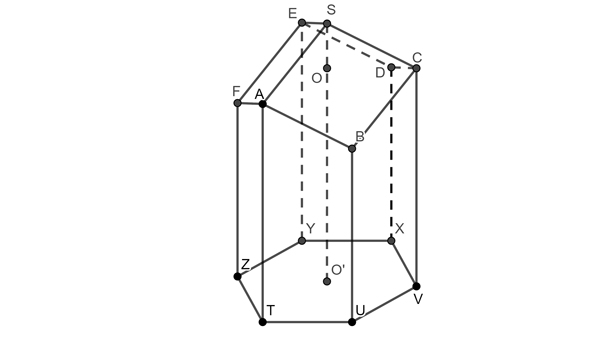
L’alvéole au complet.

Les points A, C, E d’une part, B, D, F d’autre part sont dans des plans parallèles à celui de l’hexagone. Ainsi, AT = CV = EY et BU = DX = FZ, ce qui a pour conséquence que SABC, SCDE et SEFA sont trois losanges isométriques : ils forment le fond de l’alvéole.

Le volume est facile à calculer : faire pivoter la face SABC autour de la diagonale [AC] amène le point S en S’ et B en B’. Les tétraèdres bleu et rouge ayant même volume, le volume total de l’alvéole n’a pas changé et il reste encore le même pour une alvéole à fond plat, dont on trouve sans problème le volume.

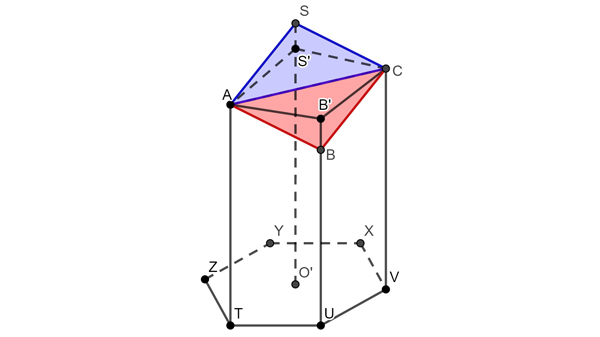
Calcul du volume total de l’alvéole.

Un calcul qui ne manque pas d’aire

Envisageons maintenant l’aire totale de cette alvéole. Posons OO’ = h et OS = x, en prenant la longueur des côtés de l’hexagone de base comme unité. L’étude de la droite des milieux [II’] du trapèze SO’UB montre que SO’ + UB = 2II’ = 2AA’, ou encore h + x + UB = 2h, d’où UB = h – x.

La surface de l’alvéole est constituée de six trapèzes comme ATUB, et de trois losanges comme SABC. L’aire de chaque trapèze est égale à

\( \dfrac{(\text{AT} \times \text{BU}) \times {\text{TU}}}{2}\)
 soit 

\( \dfrac{2h -x}{2},\)

celle de chaque losange à 

\( \dfrac{\text{SB} \times \text{AC} }{2}.\)

Les calculs donnent

\( \text{AC} = \sqrt{3}\)
et

\( \text{SB} = \sqrt{1+4x^2},\)

d’où l’aire d’un losange :

\( \dfrac{\sqrt{3}}{2} \sqrt{1+4x^2}.\)

Ainsi, l’aire totale S(x) de l’alvéole ouverte est égale à

\( \text{S} (x) =6h -3x+ \dfrac{3\sqrt{3}}{2} \sqrt{1+4x^2}.\)  

Cela définit une fonction dérivable sur l’ensemble des réels positifs, dont la dérivée S’(x) est égale à

\( -3 + \dfrac{3\sqrt{3}}{2} \dfrac{2x}{ \sqrt{1+4x^2}}.\)  

La dérivée S’(x) s’annule pour

\( x = \dfrac{1}{\sqrt {8}}.\)

La fonction S commence par décroître, puis croître ensuite, pour atteindre son minimum en cette valeur. 

Ce n’est pas tant la valeur de ce minimum (à savoir \( 6h + \dfrac{3}{\sqrt{2}}\)   ) qui est intéressante, mais l’angle en S de chacun des trois losanges du fond, le fameux « angle des abeilles ». On en obtient aisément la tangente :

\( \tan \dfrac {\widehat {\text{ASC}}}{2} = \dfrac{\text{AC}}{\text{SB}}= \sqrt {2},\)

ce qui fournit une valeur de l’angle voisine de 109°28’. On en déduit la valeur de l’autre angle des losanges, dont la tangente de l’angle moitié est l’inverse de la précédente, soit \( \widehat {\text{SAB}} \simeq \)  70°32', l’angle supplémentaire de \( \widehat {\text{ASC}}.\)  Les cellules vont donc exactement s’emboîter, et avec une surface minimum. Pas bêtes, les abeilles !

Que la forme géométrique des alvéoles soit « absolument parfaite en économisant la main d’œuvre et la cire », comme le disait Charles Darwin, il n’est plus possible d’en douter plus maintenant. La question se pose encore aux chercheurs de savoir si cette « perfection » tient plus à l’habileté et à l’intelligence des butineuses qu’aux propriétés physiques de la cire.

[encadre]

Les abeilles dans l'histoire

Dans l’Antiquité déjà, Aristote (au IV ^e siècle avant notre ère) dans son Histoire des animaux aussi bien que Pline l’Ancien (au I ^er siècle avant J.-C.) dans son Histoire naturelle disaient avoir remarqué la forme hexagonale des alvéoles des abeilles. C’est Pappus d’Alexandrie (au IV ^e siècle de notre ère) qui semble avoir été le premier à traiter cette question. Il le fait de façon purement géométrique, au Livre V de ses Collections.

La forme rhombohédrale du fond n’a cependant été remarquée, semble-t-il, qu’au XVIII ^e siècle, au moment où l’astronome et mathématicien franco-italien Jean-Dominique Maraldi détermine précisément les valeurs de 109°28’ et 70°32’ pour les angles optimaux des losanges. Le géomètre allemand Johann Samuel König, à la demande du physicien René-Antoine Ferchault de Réaumur, traite par le calcul différentiel le problème de « Déterminer, entre toutes les cellules hexagonales à fond composé de trois rhombes [losanges] égaux, celle qui peut être construite avec le moins de matière »… et trouve en 1739 des angles de 109°26’ et 70°34’. Le fin mot de l’histoire revient au mathématicien écossais Colin Maclaurin, qui, en traitant la question de manière purement géométrique, détecte dans les calculs de König une erreur… et donne raison aux valeurs de Maraldi. D’autres mathématiciens ont par la suite confirmé ces valeurs.

Références :

- Les angles. Bibliothèque Tangente 53, 2015.

- Découpages et pavages. Bibliothèque Tangente 64, 2018.

[/encadre]