
« Brachistochrone » : voilà un bien drôle de nom pour une courbe ! C’est pourtant beaucoup plus qu’un simple objet géométrique, c’est la solution à un problème d’optimisation qui a tenu en haleine les mathématiciens du XVII e siècle, même les plus aguerris, et qui a essaimé dans d’autres domaines pour donner finalement naissance au calcul des variations.
Chemin le plus rapide : les débuts
Le problème, au départ, s’est posé en termes simples : trouver la ligne droite que peut décrire le plus vite possible un point partant de A pour aller en B, situé sur une verticale. Il s’agit là du problème de la droite brachistochrone (composé de deux mots grecs signifiant « le plus court » et « le temps »).
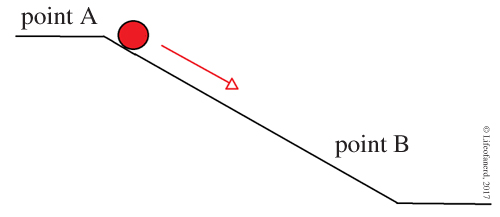
La solution est venue de Galilée qui, en 1638, dans son Discours sur deux nouvelles sciences (la mécanique ou l’étude du mouvement, et la résistance des matériaux), a calculé qu’une telle ligne devait faire avec la verticale un angle de 45°. Il calcule ensuite que si le point pesant se déplace de A vers B en utilisant des lignes droites, il atteindra B plus rapidement en naviguant le long des segments [AC] puis [BC], où C est élément d’un arc de cercle. Par contre, lorsqu’il généralise son dernier résultat en concluant « il semble possible de conclure que le mouvement le plus rapide entre deux points n’a pas lieu le long de la ligne la plus courte, c’est-à-dire le long d’une droite, mais le long d’un arc de cercle », il fait erreur, manquant sans doute des résultats de calcul différentiel qui lui auraient facilité la solution.

Il faut attendre juin1696 pour que Jean Bernoulli, qui semblait déjà connaître la solution du problème, lance, dans les Acta Eruditorum, revue scientifique mensuelle allemande, aux « plus brillants mathématiciens du monde » un défi, à trouver dans les six mois : « Étant donnés deux points A et B dans un plan vertical, quelle est la courbe décrite par un point mû par sa seule gravité, qui part de A et arrive en B dans le temps le plus court ? »
Quatre mathématiciens célèbres ont répondu à l’appel : Isaac Newton, en une soirée, paraît-il, et un peu plus tard, Gottfried Wilhelm Leibniz ayant fait prolonger le délai, les trois autres, Jacques Bernoulli, frère de Jean, Leibniz, et le marquis Guillaume de L’Hôpital.
La solution de Newton sera publiée dans Philosophical Transactions of the Royal Society, en janvier 1697, celle de Leibniz et celles des frères Bernoulli dans Acta Eruditorum en mai de la même année, celle du marquis de L’Hôpital ne sera publiée… qu’en 1988. Les travaux coopératifs de ces mathématiciens ont, avec raison, pu faire dire à Jean Bernoulli : « Mon frère aîné a été le quatrième de ceux qui, parmi trois grandes nations, Allemagne, Angleterre, France, se sont unis avec moi-même dans une si magnifique recherche, tous trouvant la même vérité. »
L’idée astucieuse de Jean Bernoulli a été de diviser le plan en bandes horizontales et de remplacer le point mobile par un rayon lumineux traversant les différentes couches et réfracté à chaque passage. Selon le principe de Fermat, la lumière suit un chemin rectiligne dans chacune des bandes et, en passant à la limite, avec des couches devenant de plus en plus minces, ces segments deviennent une courbe, que Jean Bernoulli définit par une équation différentielle, et dans laquelle il reconnaît une cycloïde tangente au départ à la verticale.
Les acteurs de la découverte
Le curriculum du problème brachistochrone commence ainsi avec Galilée (1564–1642), né à Pise (Italie), qui, en 1638, résout le problème de la ligne droite permettant de rejoindre le plus rapidement possible un point A à un point B situé sur une verticale. Il fait par contre erreur en déclarant, grâce à des considérations géométriques, que le chemin non droit le plus rapide est un arc de cercle. L’apport de Galilée à la physique et à l’astronomie a été fondamental ; son apport aux mathématiques est plutôt géométrique. Il étudie en particulier la cycloïde, et c’est à lui que l’on doit ce nom.
[encadre]
Tout savoir sur la cycloïde
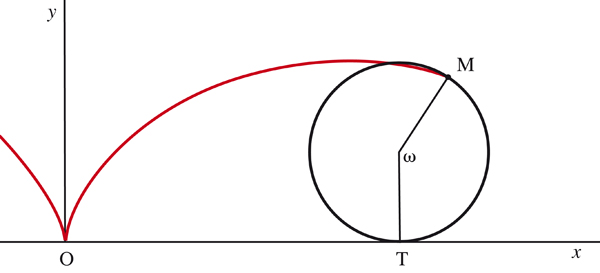
La cycloïde.
La cycloïde est la courbe décrite par un point fixé sur un cercle qui roule sans glisser sur une droite. Galilée la connaissait déjà, Pascal l’appelait « la roulette ». Elle était pour lui une courbe « tautochrone », où tous les points, d’où qu’ils soient lâchés, arrivent en bas en même temps. Il avait lancé un concours pour déterminer cette courbe avec précision ; on doit la solution à Christian Huygens en 1659.
En paramétrant avec l’angle
et en écrivant que OT = MT, on obtient ses équations paramétriques :
Sa symétrique par rapport à l’axe des abscisses est désormais identifiée comme une courbe « brachistochrone », soit la courbe de descente la plus rapide d’un point A à un point B. C’est cette coïncidence entre les deux courbes qui incite Jean Bernoulli à terminer sa recherche en disant : « Avant de terminer, je veux dire encore une fois mon admiration pour la coïncidence inattendue entre la [courbe] tautochrone de Huygens et ma [courbe] brachistochrone. […] La nature agit toujours de la manière la plus simple, ce qui nous permet de voir une seule courbe servir pour deux fonctions, alors qu’avec n’importe quelle autre hypothèse, nous aurions eu besoin de deux courbes. »
[/encadre]
L’histoire se poursuit avec Jean Bernoulli (1667–1748), né à Bâle (Suisse), qui s’intéresse à tous les domaines des mathématiques. Il est le premier à lancer le défi de la courbe brachistochrone en 1696, l’ayant lui-même déjà résolu. Il est l’un des meilleurs porte-parole du calcul infinitésimal, qu’il enseigne au marquis de l’Hôpital, et prend parti pour Leibniz dans la querelle qui l’oppose à Newton pour savoir qui, de l’un ou de l’autre, est le « véritable » inventeur du calcul intégral.
Indissociable de Jean est son frère aîné, Jacques Bernoulli (1654–1705), à qui l’on doit de nombreux travaux mathématiques, tout spécialement le développement du calcul infinitésimal, qu’il applique à l’étude des courbes. Une brouille au sujet du problème brachistochrone est d’ailleurs née entre les deux frères, Jacques estimant sa solution meilleure que celle de Jean…
Parmi les contributeurs au défi lancé par Jean Bernoulli, Isaac Newton (1643–1727), mathématicien et physicien britannique, a répondu le premier, faisant appel à la cycloïde par une méthode géométrique. Il est par ailleurs considéré comme le père fondateur, avec Leibniz, du calcul différentiel et intégral.
C’est le philosophe et mathématicien Gottfried Wilhelm Leibniz (1646–1716), né à Leipzig (Allemagne), qui a persuadé Jean Bernoulli d’accorder un délai supplémentaire pour répondre à son défi sur le brachistochrone, afin que les mathématiciens étrangers puissent y répondre également. Il donne lui aussi sa solution. Auteur d’importantes recherches, il invente de nombreuses notations mathématiques, mais est surtout connu pour son œuvre philosophique, pour lui très liée à la mathématique.
En France, le marquis Guillaume de L’Hôpital (1661–1704) a lui aussi fourni une solution au problème, publiée très tard. Fort des leçons que Jean Bernoulli lui a prodiguées, il rédige en 1696 le premier livre en français sur le calcul différentiel : Analyse des infiniment petits pour l’intelligence des lignes courbes.
Dans le parcours européen de la courbe brachistochrone figurent aussi les noms d’Eugenio Beltrami (1835–1900), mathématicien et physicien italien, dont les travaux portent entre autres sur la géométrie différentielle, du grand Léonard Euler (1707–1783), lui aussi né à Bâle, dont l’œuvre principale a été le développement de l’analyse (on lui doit le terme calcul des variations), et de Joseph-Louis Lagrange (1736–1813), né en Italie puis naturalisé français, mathématicien, mécanicien et astronome, auteur d’importants résultats en physique et surtout en théorie des fonctions.
Vers le calcul des variations
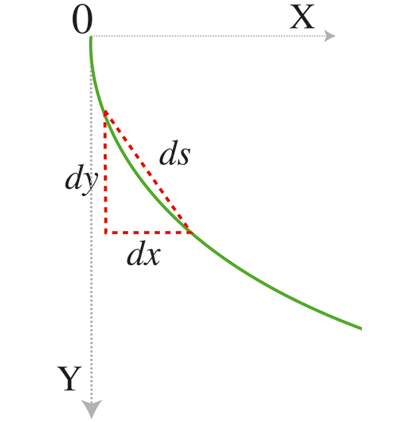
Minimiser une quantité définie par une fonction a par la suite été l’objet de fructueux échanges entre mathématiciens : Jacob Bernoulli a posé à son frère des problèmes isopérimétriques (déterminer la forme géométrique qui, à périmètre donné, maximise son aire), Euler a repris leurs problèmes pour en faire un recueil publié en 1744, dans lequel il fait intervenir l’équation différentielle dite d’Euler–Lagrange. Lagrange lui-même dans son Essai sur une nouvelle méthode pour déterminer les maxima et minima des formules intégrales indéfinies publié en 1762, cherchant une courbe pour laquelle une certaine quantité est maximale ou minimale, traite le problème avec les méthodes de calcul différentiel introduites par Newton et Leibniz : c’est le calcul des variations, tel que l’a défini Euler, que Lagrange présente dans son ouvrage en ces termes : « Le premier problème de ce type [calcul des variations] résolu par les mathématiciens est le [problème] brachistochrone, ou la courbe de plus rapide descente proposé par Jean Bernoulli à la fin du siècle dernier. »
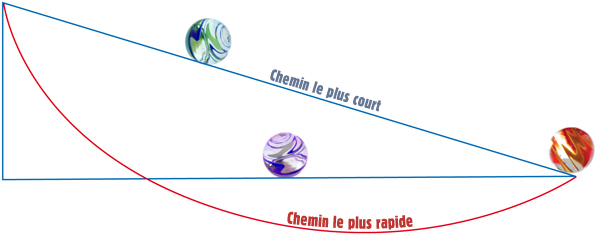
Le calcul des variations résout élégamment le problème brachistochrone.
Rappelons les données du problème :
d’où le calcul du temps de descente de A vers B :
Or,
La conservation de l’énergie impose
où g est l’accélération de la pesanteur, d’où
On pose alors
fonction particulièrement simple car elle ne dépend pas de x.
C’est un cas particulier de l’équation d’Euler–Lagrange où s’applique
l’identité de Beltrami :
est identiquement égal à une constante.
En détaillant ensuite
Cette dernière se résout en posant par exemple y’ = cotan( t / 2), d’où l’on déduit
forme paramétrée de l’équation d’une cycloïde.
Le problème brachistochrone, s’il a été à la source du calcul des variations, base sans aucun doute de la physique moderne, a aussi pour les jeunes d’aujourd’hui des applications beaucoup plus terre à terre : il a inspiré aux concepteurs des pistes de skate le profil de leurs rampes, les fameux half-pipes, dessinées pour que la descente des usagers soit la plus rapide possible.
