D’où vient la topologie ; à quels besoins répond-elle ? Comme pour de nombreux concepts, il n’existe pas de création ex nihilo mais au contraire des approches successives qui rendent incontournable le besoin de faire de notions imprécises une théorie bien construite.

On peut situer les premiers balbutiements avec Gottfried Wilhelm Leibniz, à la fin du XVII ^e siècle, lorsque le savant et philosophe allemand a souhaité créer une nouvelle géométrie, qu’il nomme analysis situs, différente de celle d’Euclide et de Descartes, qui ne serait pas un « calcul des magnitudes » mais un « calcul des situations ».

En tentant, certes très maladroitement, de définir une notion de limite pour justifier la notion de « différentielle », Leibniz s’est penché sur un autre aspect, que l’on traite désormais par des considérations topologiques. Cette recherche s’est poursuivie avec Jean Le Rond D’Alembert au siècle suivant, puis Augustin Louis Cauchy et Karl Weierstrass dans le courant du XIX ^e siècle.

Une approche très différente a été engagée par Leonhard Euler avec son fameux problème des ponts de Königsberg, mais ces considérations restaient certainement pour lui très anecdotiques.

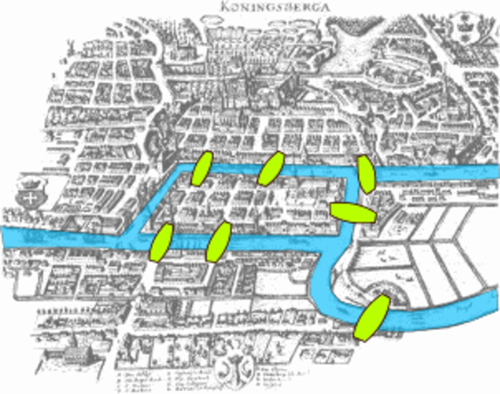
Le problème des sept ponts de Königsberg consiste à savoir s’il est possible à un promeneur d’emprunter une fois, et une seule, chacun des ponts de la ville et de revenir à son point de départ. La réponse, négative, a été apportée par Euler en modélisant la question à l’aide d’un graphe.

Spécialiste de géométrie projective (très en vogue en Allemagne au milieu du XIX^e siècle), August Möbius s’intéressait quant à lui à des surfaces atypiques, comme son célèbre ruban (voir l'article Ceci n'est pas un ruban de Möbius !), qu’il exhibe en 1848.

Une nouvelle conception de l’espace

Dénouer les mystères des déformations caoutchouteuses), où sont décrites des surfaces, souvent « trouées », que l’on déforme, et l’austérité des axiomes qu’on lui assène en général lors du premier « cours de topo » (voir l'encadré Topologie versus analysis situs). Même avec du recul, le lien reste souvent pour lui difficile à établir. Pour bien le comprendre, faisons appel au principe que Felix Klein (en photo ci-contre) a présenté en 1872 connu sous le nom de programme d’Erlangen. Le mathématicien allemand définit une géométrie comme les invariants d’un groupe de transformations de l’espace. Qu’entend-on par là ? La géométrie qui nous est la plus familière est celle régie par les isométries, ces applications qui conservent les distances et les angles. Les cercles d’un rayon donné en sont un invariant (l’un est l’image de l’autre par une isométrie). Cette vision de l’espace nous est familière car elle ne déforme pas les objets, c’est donc la mieux adaptée à l’étude des mouvements et pour nous la plus intuitive. Sauf accident, notre véhicule conserve la même forme, de même qu’un certain nombre d’objets. Ceci ne décrit cependant pas toute la réalité.

Lorsque l’on « zoome », on autorise un changement d’échelle ; le groupe des similitudes est alors mieux adapté. Lorsque l’on prend une photo, c’est le groupe projectif qui prend le relais et l’on sait que l’image d’un cerceau n’est alors en général pas un cercle.

La topologie est associée à un groupe beaucoup plus large, celui des homéomorphismes, c’est-à-dire des applications continues ainsi que leur réciproque. En d’autres termes, on s’intéresse à la déformation d’une figure obtenue continûment, c’est-à-dire sans « saut », sans « déchirure ». L’élastique en est un excellent exemple… tant qu’on ne le rompt pas. Dans l’exemple des ponts de Königsberg, seule la position des ponts entre eux et par rapport aux îles revêt de l’importance ; avoir le plan précis de la ville n’a aucun intérêt pour résoudre le problème. Cela surprendra les non-initiés mais la topologie est une géométrie ; elle en est une avec un regard qui nous dérange un peu puisque la notion de figure y prend un sens différent ; un cercle et un carré sont indistinguables puisque une déformation continue transforme l’un en l’autre. Cependant, ce qui aurait pu paraître un amusement de mathématiciens nostalgiques de la pâte à modeler de leur enfance s’est avéré d’une importance extrême pour le développement des maths aux alentours de 1900.

Sans notion de distance !

Ainsi, la topologie, c’est-à-dire la science des lieux, a pour objet de définir des notions de proximité… sans définir de notion de distance ! Mais pourquoi donc se priver de cette notion si simple et tellement intuitive ? On le fait pour plusieurs raisons. La première est liée à l’aspect arbitraire de la distance : non seulement on peut changer d’unité de mesure (mais ce n’est pas bien grave), on peut aussi étirer l’espace à certains endroits et le rétrécir à d’autres sans modifier les notions sous-jacentes que l’on veut étudier. La seconde, plus fondamentale, est que l’objet de la topologie s’applique à des notions plus générales que l’espace qui nous environne. Elle concerne aussi des figures géométriques. Pour définir géométriquement la tangente à une courbe, on aime à le faire comme position limite d’une droite. On s’intéresse aussi à définir la limite d’une suite de fonctions, de suites. Les notions d’intégration et de dérivation sont elles aussi obtenues par des limites d’objets mathématiques sur lesquels des notions de distance seraient difficiles (ou même parfois impossibles) à définir et apparaîtraient comme totalement arbitraires.

Aussi deux pistes se sont dégagées entre 1850 et 1914, l’une purement géométrique mais avec des préoccupations totalement novatrices, l’autre tournée vers les études de fonctions et plus généralement vers l’analyse mathématique.

Poincaré et la topologie algébrique

Sur les hypothèses qui servent de fondement à la géométrie, il élabore une conception révolutionnaire de la géométrie considérée dans son sens le plus large. Plutôt que de caractériser les géométries non euclidiennes par la négation du cinquième postulat d’Euclide (comme l’ont fait Nikolaï Ivanovitch Lobatchewski et János Bolyai), il définit une métrique locale, c’est-à-dire en chaque point, par l’expression de la variation infinitésimale de la distance en fonction des coordonnées. On peut donc « étirer » ou « rétrécir » l’espace ou la surface. Au passage, Riemann distingue les propriétés d’étendue des notions métriques. Les premières correspondent à ce que nous nommons la topologie.

homéomorphes, c’est-à-dire peuvent être considérées topologiquement identiques, ou si elles ne le sont pas. Pour ce faire, il a associé à chacune d’entre elles un groupe dit d’homotopie et ramené ainsi ce problème géométrique à de l’algèbre. Sa célèbre conjecture énoncée en 1904 portait sur ce sujet ; elle ne fut démontrée qu’en 2002 par le mathématicien russe Grigori Perelman.

 

La science des lieux

L’étude des fonctions a pris son essor de manière spectaculaire entre 1850 et 1900. Des définitions précises ont été établies, en particulier grâce à Karl Weierstrass et bientôt, sous la houlette de mathématiciens italiens, on s’est penché sur des espaces dont les éléments sont des fonctions. Le besoin de définir la notion de limite dans ces espaces, d’étudier la continuité d’une fonction (on dit alors un opérateur) dont l’argument varie dans l’ensemble des fonctions, demandait de concevoir une notion plus générale de continuité et de limite.

écart) dans des espaces qu’il qualifie d’abstraits ; il y définit la notion de partie compacte, très utile pour traiter des problèmes d’extremums d’une fonction et de justifier qu’ils sont atteints. Cette formalisation proposée par Fréchet s’avère, dans certains cas, trop rigide, la notion de limite ne nécessitant pas une condition si forte.

Felix Hausdorff comprend alors le rôle que peut jouer la théorie toute naissante des ensembles pour définir une notion de voisinage. Dans son ouvrage Principes fondamentaux de la théorie des ensembles publié en 1914, il propose une définition abstraite de la topologie ne faisant appel qu’aux notions ensemblistes de l’espace. Il adapte la notion d’ensemble compact dans ce nouveau cadre. De nos jours, on préfère une définition basée sur la notion de partie ouverte ; elle est totalement équivalente à celle de Hausdorff. Partant de l’axiomatique du mathématicien allemand, il suffit d’appeler ouvert toute partie qui est un voisinage de chacun de ses points.

Timbre hommage à René Maurice Fréchet.

L’analyse mathématique utilise désormais très largement la notion d’espace topologique ; dans les années 1920 sont introduits les espaces vectoriels normés mais aussi les espaces hilbertiens, structures qui s’inscrivent totalement dans le cadre ouvert par Hausdorff. Cette nouvelle conception de l’espace a permis de clarifier un nombre inouï de notions dans de nombreux champs des mathématiques.