Étymologiquement, la géométrie est liée à l’idée de mesure. Mais l’étude des objets qui nous entourent se limite-t-elle vraiment à une approche métrique ? 

Un objet élastique ne conserve-t-il pas, lui aussi, certaines propriétés quand il est déformé ? Les mathématiciens ont apporté des réponses à toutes ces questions en développant une des branches les plus fécondes qui soient : la topologie.

Des jeux de maths à modeler

Qui n’a jamais joué avec un peu de pâte à modeler dans son enfance ? N’est-il pas amusant de déformer un terrifiant dinosaure en naïf petit lapin ? Les mathématiciens aussi savent s’amuser, mais ils aiment bien ajouter quelques contraintes. 

 Ainsi peut-on se poser la question suivante : étant donné deux sculptures en pâte à modeler, est-il possible de passer de l’une à l’autre de façon continue ? 

Attention, tout doit se faire en douceur. 

Conformément aux contraintes, le dé présente des cuvettes pour marquer les faces (il n’est pas « troué »).

Les transformations trop brutales sont bannies : on ne peut pas couper ou percer les sculptures considérées, et toute transformation doit être réversible. 

Par contre, on ne se soucie pas du tout de la conservation du volume (la pâte à modeler peut devenir plus ou moins dense). L’étude des objets de ce point de vue est la topologie. En respectant ces règles, on peut passer d’une boule à un dé ou à une étoile de mer, et réciproquement.

On peut aussi passer d’un beignet à une tasse plus ou moins informe.

En revanche, on voit mal comment passer de la boule au beignet (que les mathématiciens appellent un tore plein) sans enfreindre les règles du jeu. On dit dans ce cas que ces objets ne sont pas homéomorphes (qu’ils n’ont donc pas la « même forme »).

Tout cela semble assez naïf. Mais reconnaissez-vous, au premier coup d’œil, notre tore plein sur l’image ci-dessous ? Pourtant, c’est bien lui…

Enfin, comment réussiriez-vous à montrer que l’on peut, ou que l’on ne peut pas, libérer l’un des deux anneaux du ruban rouge ci-dessous en respectant les règles de la topologie ? 

Une avancée… fondamentale

En 1895 entre en scène un jeune académicien qui vient à peine de dépasser la quarantaine. Cet homme remarquable n’est pas un inconnu et ses talents ne sont déjà plus à prouver : mathématicien, physicien, ingénieur, géodésien, philosophe, citoyen engagé, il est souvent considéré comme l’un des tout derniers savants universels, maîtrisant toutes les branches des sciences qu’il aborde. Il propose dans son mémoire Analysis situs une idée spectaculaire. Parti de l’étude d’épineuses équations différentielles a priori éloignée de nos problèmes de pâte à modeler, Henri Poincaré se trouve confronté à des questions de topologie…

Henri Poincaré (1854–1912) apportera des compléments à son mémoire de 1895 jusqu’en 1904.

Considérons l’exemple d’une bouée (un tore creux) pour comprendre sa démarche. On peut tracer sur cette surface des chemins qui partent d’un point A et qui y reviennent. On appelle ces chemins fermés des lacets. Comme on est en topologie, on ne distinguera pas deux lacets si l’on peut déformer continûment le premier pour obtenir le second sans sortir de la surface ; on dit alors que ces lacets sont homotopes.

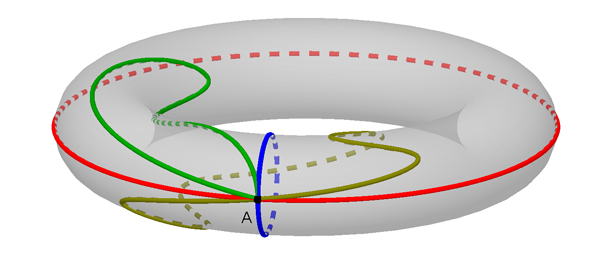
Le lacet bleu est homotope au lacet beige, mais pas au lacet rouge ni au lacet vert.

Le lacet consistant à partir du point A et à y rester est le lacet trivial. Certains lacets sont homotopes au lacet trivial : on peut les rétracter complètement au point A. Le lacet vert dessiné sur le tore ci-dessus est un exemple de lacet homotope au lacet trivial.

Poincaré analyse alors ces familles de lacets en les dotant d’une structure algébrique particulière : c’est le groupe fondamental de l’objet. Cela peut sembler obscur mais c’est en fait une idée lumineuse, car si deux objets sont homéomorphes, alors leurs familles de lacets se comportent « de la même façon » : les deux objets ont le même groupe fondamental. Poincaré vient d’associer un invariant algébrique à chaque sculpture en pâte à modeler, c’est-à-dire un objet algébrique qui reste le même si l’on déforme continûment la sculpture.

L’étude délicate des questions de topologie est alors ramenée à celle des groupes, une notion bien connue et étudiée par les mathématiciens depuis le début du XIX^e siècle.

À titre d’exemple, on peut constater que le groupe fondamental de la sphère se réduit au groupe constitué d’un seul élément (le lacet trivial), alors que ce n’est pas le cas du tore (voir en encadré). Ces deux objets sont bien différents : ouf !

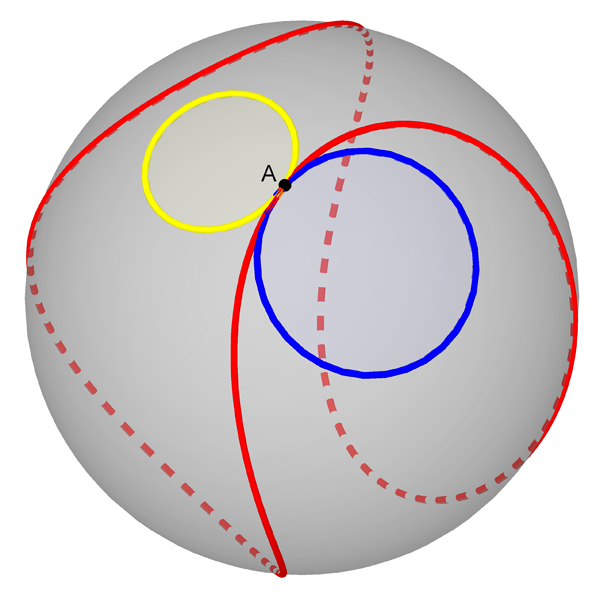
Sur la sphère, tout lacet peut se rétracter au point A, ce qui n’était pas le cas sur le tore avec le lacet bleu par exemple.

Le nœud du problème

Prenez maintenant une ficelle, emmêlez-la comme bon vous semble et collez ensemble les deux extrémités. Vous venez d’obtenir un nœud (mathématique). Les topologues se posent alors la question suivante : étant donné deux nœuds, peut-on déformer l’un en l’autre sans couper la ficelle ?

Souvenez-vous de la version légèrement biscornue du tore au début de cet article : ici non plus, il n’est pas facile de reconnaître deux objets identiques.

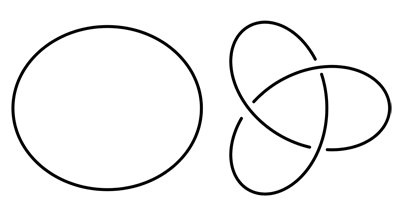
Le nœud trivial et le nœud de trèfle ne sont pas les mêmes.

Les outils introduits par Poincaré permettent de répondre au problème de reconnaissance des nœuds. L’astuce consiste à déterminer le groupe fondamental de l’espace dans lequel se trouve le nœud, ce qui revient à analyser comment on peut « se promener autour d’un nœud » sans jamais le couper.

Hélas, le groupe fondamental ne permet pas de distinguer tous les nœuds. Ainsi, avec quelques calculs, on peut démontrer que les deux nœuds ci-dessous, construits en recollant des nœuds de trèfle de deux façons différentes, ne sont pas homéomorphes… alors que les groupes fondamentaux associés sont les mêmes.

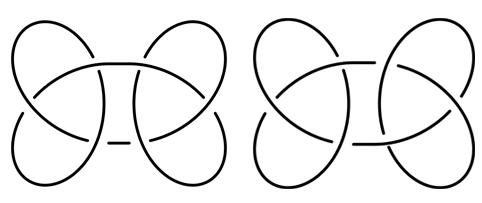
Le nœud carré (à gauche) et le nœud de vache ne sont pas homéomorphes ; 
pourtant ils possèdent le même groupe fondamental.

Le groupe fondamental n’est donc pas un invariant parfait. Est-ce un drame pour autant ? La situation était si inconfortable que s’est développée, tout au long du XX^e siècle, la topologie algébrique, domaine dans lequel on croise quelques-uns des plus brillants mathématiciens. Pour de nombreuses applications, en effet, disposer d’un invariant parfait (et facile à calculer) serait d’une portée inestimable.

L’ADN, un vrai sac de nœuds !

Vous souvenez-vous du temps où les téléphones étaient reliés à un boîtier par un fil en spirale ? Il n’était pas rare qu’après chaque communication ce fil s’entortille sur lui-même, de plus en plus ; c’est exactement ce qui se passe pour l’ADN, cette fameuse molécule en double hélice nichée au cœur de nos cellules et sur laquelle est codée l’information génétique.

Certaines molécules d’ADN sont fermées et forment des nœuds d’une extraordinaire complexité. La topologie de l’ADN influe sur son action et son fonctionnement. Des biochimistes, comme l’Américain Nicholas Robert Cozzarelli, se sont intéressés de près à ces questions. Certaines enzymes, les topo-isomérases, sont en mesure de couper des brins d’ADN et de les ressouder dans des dispositions différentes, changeant ainsi la topologie nodale de l’ADN ! C’est notamment ainsi qu’agissent certains virus, que l’on peut donc reconnaître à leur action topologique. Si l’ADN devient « plus emmêlé », on comprend que son action en soit modifiée, et il en est de même s’il est partiellement démêlé car sa partie interne devient alors plus exposée à l’action de molécules environnantes.

 

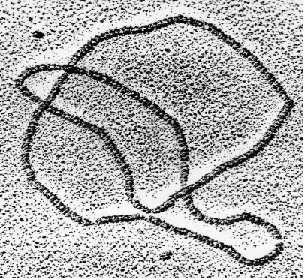
Une molécule d’ADN au microscope.

 

Résoudre les grands problèmes de théorie des nœuds et de topologie algébrique permettra-t-il de comprendre toutes les actions des topo-isomérases ? D’autres enzymes peuvent-elles agir dans un cadre différent de la théorie des nœuds ? Poincaré, fervent défenseur de l’interaction entre les différentes branches des mathématiques et des sciences, se serait sans doute enthousiasmé pour toutes ces nouvelles pistes de recherche !