Parmi les études de Felix Klein figure sa fameuse « bouteille », qui évoque irrésisti-blement un volume que l’on peut remplir. De bouteille il n’en est point car en fait un traducteur allemand s’est à l’origine quelque peu trompé, ou peut-être a voulu faire un jeu de mot, en traduisant Kleinsche Fläche par « bouteille de Klein », au lieu de « surface de Klein » (en allemand, « bouteille » se dit Flasche et surface, Fläche).
L’objet a été décrit pour la première fois en 1882.

La bouteille de Klein, tout comme l’anneau de Möbius (voir l'article Ceci n'est pas un ruban de Möbius !), est une curiosité topologique. Mais si le ruban de Möbius ne possède qu’une seule face, la fameuse bouteille, quant à elle, est telle qu’aucune distinction n’est possible entre son « intérieur » et son « extérieur ».

 

La trace du mouvement d’un cercle

Il est maintenant temps de rétablir quelques vérités. Les « surfaces » de Klein peuvent également ressembler à l’illustration suivante, vues dans un espace à trois dimensions.

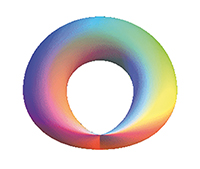
Collage d’un demi-tore avec un demi-dôme de Bohème (voir Tangente 184
et deux points de pincement (variante non symétrique).

Plus généralement, n’importe quelle surface engendrée par le mouvement d’un cercle (de rayon variable ou non) ou même d’une courbe fermée qui revient sur elle-même après rotation d’un demi-tour est une représentation de la bouteille de Klein !

La surface ci-contre est ainsi décrite par sa représentation paramétrique :

\( $$\left\{ \begin{array}{ll} x=\left ( r+\cos\frac{\theta}{2}\sin \nu - \sin\frac{\theta}{2}\sin 2\nu \right ) \sin\theta,\\ \noalign{\vspace{5pt}} y=\left ( r+\cos\frac{\theta}{2}\sin \nu - \sin\frac{\theta}{2}\sin 2\nu \right ) \sin\theta,\\ \noalign{\vspace{5pt}} z= \sin\frac{\theta}{2}\sin \nu + \cos\frac{\theta}{2}\sin 2\nu .\cr \end{array} \right.$$\)

où r est le rayon du cercle en mouvement,  \( \theta\)  est l’angle de rotation, et  \( \nu\)  indique la position du point de contact sur la section transversale.

Bouteille de Lawson–Klein.

Les bouteilles de Klein sont étroitement liées au ruban de Möbius et à des immersions du plan projectif réel, comme par exemple la surface de Boy. C’est l’un des exemples les plus simples de variété abstraite, car c’est une surface qui ne peut être représentée convenablement dans l’espace à trois dimensions.

Mathématiquement, on dit qu’elle possède une immersion de classe C^∞ dans l’espace \( \Bbb{R}^3\)  de dimension 3, mais n’y possède pas de plongement continu. Sa caractéristique d’Euler–Poincaré est nulle (voir Tangente 174).

 

Une construction… abstraite !

Une méthode de construction de la bouteille de Klein peut être de recoller deux rubans de Möbius le long de leurs bords. De manière équivalente, la bouteille de Klein est la somme connexe de deux plans projectifs.
 

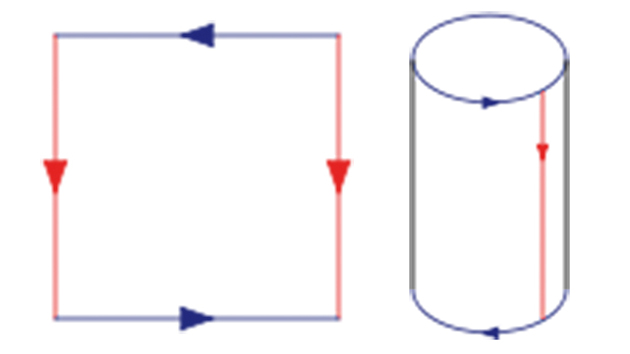
On se donne deux carrés, comme ci-dessus, et on obtient deux exemplaires de ruban de Möbius en faisant d’abord l’identification suivant les flèches bleues. Chacun de ces rubans a alors « un seul bord », les côtés verticaux rouges, qui ont été connectés à la suite de l’identification précédente. Recoller les deux rubans suivant leurs bords peut alors être considéré comme équivalent à recoller le bord droit du second carré au bord gauche du premier (et vice versa). On retrouve alors bien le cylindre, mais avec l’identification des bords bleus déjà effectuée, c’est-à-dire la bouteille de Klein.
Il est d’ailleurs plus aisé de voir qu’une bouteille de Klein coupée en deux dans le sens de la hauteur fournit bien deux rubans de Möbius…


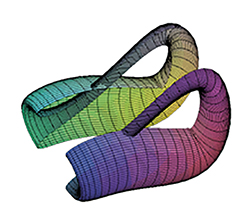Bouteille de Klein séparée selon son plan de symétrie en deux bandes de Möbius.


Lorsque l’on essaie de visualiser la bouteille de Klein dans un espace à trois dimensions, on se représente une surface qui « s’auto-intersecte ». Néanmoins, si l’on raisonne avec l’aide d’une quatrième dimension, il suffit d’imaginer qu’à l’intersection, la bouteille passe « dessus » et « dessous » au sens de cette quatrième dimension, et donc ne « s’auto-intersecte » pas. Il n’y a ni croisement de courbes, ni intersection de surfaces.
On peut ainsi en quelque sorte considérer que la bouteille de Klein est une surface qui « fait un nœud ». En tant que surface (objet à deux dimensions), il lui faut quatre dimensions pour faire un nœud, de même que pour une courbe (objet à une dimension) il faut trois dimensions pour faire un nœud.

 

La singularité des bouteilles entraîne des applications inattendues. Ainsi, le problème des trois maisons est soluble sur la bouteille de Klein, contrairement au plan. En d’autres termes (plus techniques), on peut tracer, sans croisement d’arêtes, le graphe biparti K_3,3 sur la bouteille de Klein.
Cet objet étonnant inspire artistes, infographistes, concepteur de jeux, publicistes en tant qu’objet impossible. L’ethnologue Claude Levi-Strauss (1908–2009) en a même fait une interprétation psychanalytique, comme métaphore des orifices corporels !
Le graveur d’équations Patrice Jeener en a fait l’un des objets emblématiques de son œuvre. Plus récemment, l’artiste californien 3D Erik Anderson a conçu une œuvre à partir de bouteilles de Klein enchaînées (voir ci-dessous). Les surfaces mathématiques, même abstraites, n’ont pas fini de nous étonner, et donc de nous inspirer.