Les amateurs de mathématiques ont tous au moins une fois dans leur vie réalisé un ruban de Möbius. C’est le genre d’objet mathématique remarquable que l’on réalise durant les ateliers de maths récréatives. Il s’agit de prendre une longue bande de papier, de lui faire subir une torsion d’un demi-tour, et de coller ensemble les deux extrémités ; on obtient alors une surface topologique déroutante, constituée d’une seule face (techniquement, on dit qu’elle est non orientable).

ruban paradromique, d’anneau de Bengale, ou encore de boucle afghane. Il existe même une représentation de ce fameux ruban, en bonne compagnie du dieu du temps Aion, datant de l’époque romaine tardive (III ^e siècle de notre ère).

Pour créer un anneau de Möbius, il suffit donc de découper dans une feuille de papier un rectangle allongé et de coller ensemble les côtés les plus courts, après y avoir exercé une demi-torsion. Pourtant, Tangente va vous dévoiler un secret : l’anneau que l’on crée de cette façon n’est pas véritablement un ruban de Möbius ! Car un objet « concret », matériel, ne pourra jamais être un ruban de Möbius. Qu’on le veuille ou non, cet anneau – ou plutôt surface à une seule face – est un plan recourbé dans la troisième dimension, et un plan ne peut avoir d’épaisseur, fût-elle de quelques dixièmes de millimètre comme c’est le cas d’une feuille de papier.

Un problème de canalisation

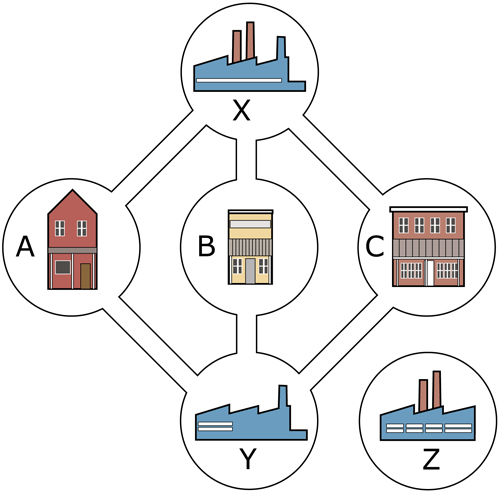
Prenons en considération l’un des problèmes insolubles que tous, plus ou moins, connaissent : l’énigme des trois maisons. Ce problème se résume ainsi : est-il possible de relier un lotissement de trois maisons A, B et C à des fournisseurs de services en eau, gaz, et électricité (notés respectivement X, Y, Z) sans croiser les canalisations ? L’impossibilité de résoudre l’énigme est une conséquence du théorème de Jordan. Toutefois, ce théorème ne s’applique pas si l’espace n’est pas orientable, comme c’est le cas pour le ruban de Möbius.

Le théorème de Jordan, dû au mathématicien français Camille Jordan (1838–1922), énonce que toute courbe fermée du plan qui ne se recoupe pas (ou courbe de Jordan ; pensez à un cercle, un carré, une ellipse…) sépare le plan en trois parties disjointes : la courbe elle-même, son intérieur (qui est borné), et son extérieur (qui n’est pas borné). Intuitivement évident, ce résultat est en fait difficile à démontrer, à cause de l’existence de courbes pathologiques (de type « fractales »), qu’il faut traiter avec grand soin.

Revenons à notre problème. Déjà, avec seulement deux fournisseurs de service, il se crée une courbe de Jordan dans laquelle se trouve incluse une maison qui ne pourra pas être reliée par un troisième fournisseur de services sans déjouer la règle du jeu.

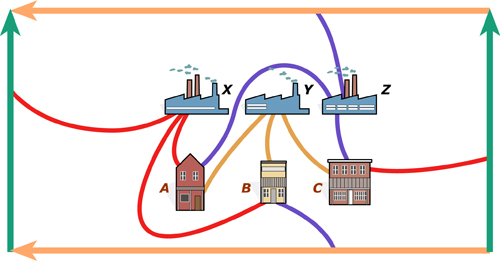
Transposition du graphe sur le tore (surface orientable), obtenu en recollant les deux bords opposés d’un rectangle.

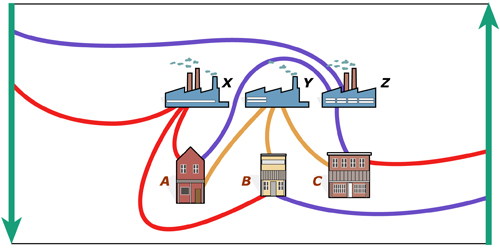
Transposition du graphe sur le ruban de Möbius (surface non orientable).

À vue d’œil, les schémas laissent apparaître que, de cette façon, l’énigme est enfin résolue. Construisons maintenant un modèle « maison » du tore en suivant les indications de la figure suivante ; là, on peut remarquer que, effectivement, toutes les maisons sont reliées aux trois fournisseurs de services sans que les lignes qui les joignent s’entrecroisent.

Quand Möbius fait des bulles de savon…

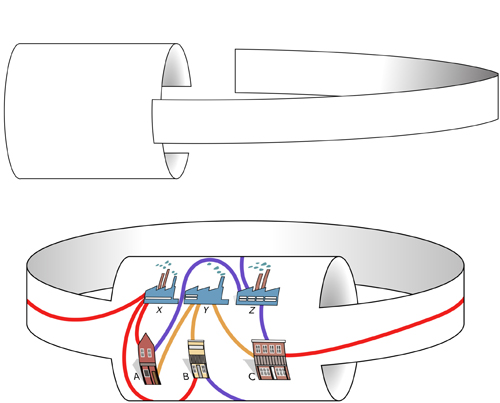
Essayons maintenant de construire un anneau de Möbius en y incorporant le graphe ; on constatera assez rapidement qu’il se forme une courbe de Jordan (mise en évidence en rose clair sur le schéma), qui empêchera le troisième fournisseur de service de joindre une des maisons sans croiser la fatidique ligne rouge. La seule façon de résoudre l’énigme est d’utiliser un astucieux subterfuge, que vous pourrez admirer sur le schéma qui suit.

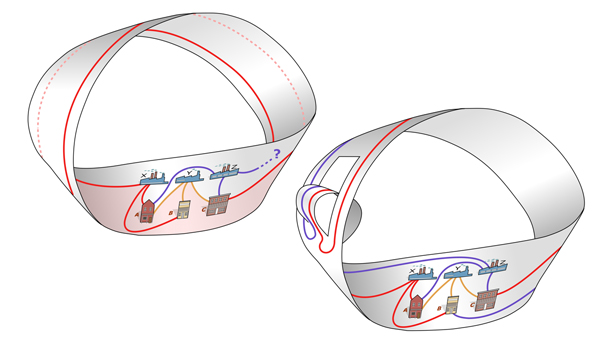
L’astuce consiste à pratiquer une incision pour créer une « languette ». Évidemment, la surface ainsi obtenue n’est plus topologiquement équivalente à un ruban de Möbius !

Vous l’aurez compris, la consistance de la surface d’un vrai anneau de Möbius est plus proche, sans être pour cela identique, de celle d’une bulle de savon… Les représentations tridimensionnelles d’un anneau de Möbius, dont certaines sont très artistiques, ne sont donc que de piètres approximations. Mais devons-nous, par rigueur mathématique, renoncer à l’utilisation des modèles tridimensionnels ? Certes non, mais il faut lors de leur utilisation être conscient qu’un modèle matériel sera, de par sa nature, toujours différent du concept abstrait qu’il est censé représenter.

Sculpture en marbre de Keizo Ushio (à gauche) et sculpture en pierre de Max Bill.