Un programme informatique est dit récursif s'il demande sa propre exécution au cours de son déroulement. Sans aucun exemple, cette phrase est difficile à comprendre… et il est encore plus difficile de saisir pourquoi aujourd'hui les langages de programmation utilisent tous la récursivité alors que les premiers, comme Cobol, pour la gestion, ou Fortran, pour le calcul scientifique, s'en passaient. L'une des raisons est la sûreté des programmes récursifs, pratiquement les seuls dont on puisse démontrer qu'ils font bien ce qu'ils sont censés faire…

Récurrence et jeux de cartes

Prenez un jeu de cartes, mélangez-le puis essayez de le trier. Comment faire ? A priori, la tâche est complexe. Le principe de récurrence permet de la simplifier considérablement en posant la question autrement : imaginez que vous sachiez trier n cartes, comment en trier n + 1 ? Plus prosaïquement, vous savez trier un jeu de quatre cartes. On vous en donne une de plus ; que faites-vous ?

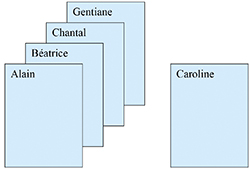
Bien entendu, vous triez les quatre premières puis insérez la cinquième à sa place. Pour cela, il suffit de la comparer successivement avec les cartes déjà triées en commençant par la première. Ici, la nouvelle carte s'insère après la deuxième. Cette méthode repose exactement sur l'idée de récurrence ! Pour vous en convaincre, formalisons-la dans le style des démonstrations par récurrence. Voici donc une méthode qui, pour la donnée d'un jeu de cartes T, renvoie le même jeu trié :

Tri (T) : Si le nombre n de cartes est égal à 1, renvoyer T (car le jeu est trié), sinon priver le jeu T de son dernier élément x de façon à obtenir un jeu T' et Insérer (x, Tri (T')) où Insérer (x, Tri (T')) insère une carte dans un jeu trié.

Comment être sûr que cet algorithme fonctionne quel que soit le jeu de cartes donné ? La réponse tient encore dans le principe de récurrence (voir en encadré).

Ce principe est souvent utilisé en « divisant par 2 ». Pour résoudre un problème pour n, on suppose que l'on sait le résoudre pour n / 2 (quotient entier de la division de n par 2, ainsi 5 / 2 = 2). Imaginons que vous vouliez classer huit fiches comportant chacune un nom. Une idée est de couper le jeu en deux jeux de quatre fiches, et de donner ces deux jeux à classer à deux amis. Admettons qu'ils vous renvoient les deux jeux triés ci-contre.

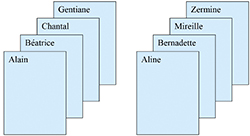
Comment trier un jeu composé de deux parties triées ? Le travail est en fait fort simplifié. Il suffit de commencer par la première carte des deux jeux (ici celle du premier jeu) puis de recommencer. Après huit comparaisons, les deux jeux sont fusionnés en un seul jeu trié. Bien entendu, cette méthode repose sur une hypothèse : les deux amis renvoient les deux jeux triés. Comment peuvent-ils faire ? La réponse semble absurde : faire appel à deux amis. Ceux-ci vont se trouver avec deux cartes dans les mains. Quoi de plus simple à trier ? Ou bien, elles sont dans l'ordre, ou bien on les permute pour les y mettre. La méthode repose encore sur l'idée de récurrence :

Tri (T) : Si le nombre n de cartes est égal à 1, renvoyer T (car le jeu est trié), sinon diviser le jeu en deux jeux T₁ et T₂ (le premier a n / 2 cartes), renvoyer Fusion (Tri (T₁), Tri (T₂)) où Fusion (T₁, T₂) fusionne deux jeux triés en un jeu trié suivant la méthode décrite ci-dessus. Le principe de récurrence permet encore de prouver que cet algorithme fonctionne quel que soit le jeu de cartes donné.

Dans tous les langages modernes

 La même démarche permet de créer des algorithmes, avant de les prouver. L'important est de rester au cœur du principe : si l'on sait passer de l'étape n à l'étape n + 1 et que l'on sait démarrer, on peut traiter toutes les étapes. Quand on l'applique en informatique, on ne parle plus de récurrence mais de récursivité. On peut ainsi définir des fonctions récursives dans pratiquement tous les langages modernes. L'exemple le plus souvent donné est celui de la fonction factorielle :

Fonction Factorielle, argument n : nombre

Si n = 0 alors Factorielle := 1 sinon
Factorielle := n × Factorielle(n – 1).

Comme dans un grand nombre de langages, on fait précéder la description de la fonction par une partie déclarant son nom (Factorielle) et son ou ses arguments (n, qui est un nombre). Le corps de la fonction décrit comment elle est définie. Cette définition peut sembler absurde, car la factorielle y est définie à partir d'elle-même. On la comprend mieux en pensant à une délégation de tâche. Vouloir suivre son exécution est fastidieux et, de plus, ne sert à rien. L'intérêt est de pouvoir prouver que la fonction Factorielle remplit bien son rôle. Cela se fait par récurrence sur son argument n. En fait, l'écriture de la fonction est elle-même la preuve qu'elle donne bien le bon résultat !

En effet, si n = 0, le résultat est bien 1. Admettons que le résultat soit bien (n – 1)! pour n – 1, la relation Factorielle := n × Factorielle(n – 1) donne n (n – 1)! = n! pour n, ce qui est le résultat attendu. Par récurrence, la fonction Factorielle renvoie donc toujours le bon résultat.

Une question où la meilleure réponse tient dans la récursivité a été conçue comme un casse-tête par son inventeur, Édouard Lucas. Il s'agit des tours de Hanoï, dont le nom n'a rien à voir avec cette ville, juste avec la fantaisie de Lucas. Dans ce jeu, on dispose de plusieurs rondelles de rayons différents et de trois piquets sur lesquels les rondelles peuvent être enfilées. Au départ, les rondelles sont sur le piquet de gauche dans l'ordre des rayons décroissants, la plus large en bas. Chaque coup consiste à déplacer la rondelle du sommet d'une pile au sommet d'une autre en ne la posant que sur une rondelle plus grande. Le but du jeu est d'arriver en un nombre fini de coups à la configuration initiale, mais sur le piquet de droite. Le problème est d'autant plus compliqué que le nombre de rondelles est grand.

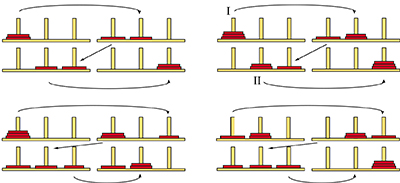
Commençons donc par le cas de deux rondelles. Quelques essais mènent facilement à une suite de trois coups. Passer au cas de trois rondelles semble très compliqué. On reprend ici l'idée exploitée dans le cas du tri. Comment faire en supposant qu'on sache le faire pour deux rondelles ? On recommence donc en considérant les deux rondelles supérieures comme une unité. La solution proposée est a priori illégale… mais elle permet de trouver une solution licite (le déplacement de deux rondelles est possible d'après la solution du jeu avec deux rondelles). En fait, il s'agit d'ajouter des positions intermédiaires. Par exemple, entre la première et la seconde étape du tour de prestidigitation. Ainsi la transformation I est réalisée en bas à gauche et la II en bas à droite. En regroupant le tout, on obtient une solution en sept coups pour trois rondelles. Pour n rondelles, on obtient ainsi une solution en 2n – 1 coups… ce qui rend le jeu humainement irréalisable dès que l'on dépasse les sept rondelles.

Ces quelques exemples justifient l'affirmation : avec la récursivité, programmer, c'est prouver !