
À la Renaissance, Galilée écrivit sur une question posée par un grand joueur, Cosme II de Médicis, grand-duc de Toscane, dont il avait été le précepteur. Cosme avait remarqué qu'en jetant trois dés, le total 10 sortait plus souvent que le 9. Sans suivre réellement des joueurs comme Cosme l'a fait, on peut également l'observer en simulant le jeu. Pour cela, il suffit de le programmer et de jouer virtuellement un millier de fois (voir le texte d'un programme en encadré), le résultat obtenu sera proche du résultat théorique, celui que l'on peut démontrer.
Le paradoxe de Toscane
Pourtant, il existe autant de façons de décomposer neuf et dix en somme de trois nombres entre 1 et 6, ce qui semblait contradictoire à Cosme ! Galilée trouva la raison de cette bizarrerie, connue depuis sous le nom de de paradoxe de Toscane. On peut comprendre son mécanisme en considérant le jeu de pile ou face. Si la pièce n'est pas pipée, la probabilité d'obtenir pile est égale à 1 / 2, et de même pour celle d'obtenir face. Si l'on joue deux fois de suite, chacune des possibilités PP, PF, FP et FF est équiprobable, donc leurs probabilités sont toutes égales à 1 / 4. Si l'on jette les deux pièces à la fois, les probabilités d'avoir deux piles ou deux faces sont égales à 1 / 4, mais celle d'avoir un pile et un face est égale à 1 / 2 car elle regroupe les deux cas PF et FP. Il en va exactement de même dans le paradoxe de Toscane : les décompositions de neuf et dix ne sont pas équivalentes de ce point de vue. La différence tient en la décomposition de neuf en trois fois le même nombre, ce qui est impossible pour dix.
Le calcul montre que la probabilité d'obtenir neuf est égale à 25 / 216, alors que celle d'obtenir dix est égale à 27 / 216 (soit 1 / 8). Ces deux nombres montrent que Cosme était fin observateur, et vraiment très grand joueur, car les probabilités ne diffèrent que de 1 / 108.
En effet, en jetant trois dés, on peut obtenir 9 de six façons distinctes. Trois d'entre elles correspondent à des tirages distincts (1 + 2 + 6, 1 + 3 + 5 et 2 + 3 + 4), deux à deux tirages (1 + 4 + 4, 2 + 2 + 5) et une à un seul (3 + 3 + 3). Dans le premier cas, comme six ordres sont possibles, la probabilité de chacun est de 6 / 216 (noter que 63 = 216, nombre de tous les tirages possibles). Dans le second cas, trois ordres seulement sont possibles, ce qui donne 3 / 216. Dans le dernier cas, un seul est possible, d'où une probabilité de 1 / 216. Finalement, la probabilité totale est de (18 + 6 + 1) / 216, soit 25 / 216.
Il existe également six façons d'obtenir 10, mais elles se groupent différemment. Trois d'entre elles correspondent à des tirages distincts (1 + 3 + 6, 1 + 4 + 5 et 2 + 3 + 5), trois à deux tirages (2 + 4 + 4, 3 + 3 + 4, 2 + 2 + 6), mais aucune à un seul. Le calcul précédent est modifié en (18 + 9) / 216, soit 27 / 216.
L'obtention de 10 est donc un peu plus fréquente. La théorie, l'expérience comme sa simulation le montrent. Dans ce résultat, l'expérience comme la simulation ont des statuts du même genre, mais la théorie explique mieux le phénomène.
Quand l'expérience est impossible
La simulation du jeu est au cœur de la correspondance de 1654 entre Pascal et Fermat, à propos de la question d'un autre joueur, Antoine Gombaud, chevalier de Méré, qui date souvent la naissance du calcul des probabilités. Cette question portait sur un jeu en plusieurs manches entre deux joueurs, où chacun avait misé la même somme de 32 pistoles. La somme totale devait aller au premier qui gagnait trois manches. Chaque manche pouvait être modélisée par un tirage de pile ou face car chacun avait la même chance de gagner que l'autre. Le chevalier de Méré envisageait le cas où les joueurs étaient obligés d'arrêter le jeu alors que le premier avait gagné deux fois et l'autre, une seule. Comment partager équitablement les 64 pistoles ?
Pour répondre à cette question, Pascal estima les espoirs de chacun de gagner en poursuivant le jeu de façon virtuelle. Résumons les possibilités de poursuite du jeu par un graphe, en partant d'un état (à gauche) et en envisageant à chaque étape les deux possibilités jusqu'à ce que l'un des joueurs ait gagné.
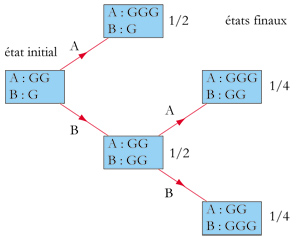
Graphe des évolutions possibles du jeu, où le premier joueur a été noté A et l'autre, B.
Le jeu peut se terminer de trois façons, qui ont chacune une probabilité d'occurrence. En tout, la probabilité de gain de A est égale à 3 / 4, celle de B à 1 / 4, donc il est équitable de donner 48 pistoles au premier et 16 au second. Ces sommes correspondent en fait à l'espérance de gain de chacun.
Des footballeurs dans le chocolat
De façon plus concrète, imaginons qu'une marque de chocolat décide de placer les joueurs de l'équipe nationale dans ses plaques de chocolat.
Elle place les onze images de façon aléatoire et se demande combien de plaques en moyenne doit acheter un amateur pour obtenir l'équipe complète. Pour résoudre le problème, on peut demander à une centaine de personnes d'acheter des plaques jusqu'à ce qu'elles aient l'équipe entière. À la fin de l'expérience, on fait la moyenne des scores obtenus ; on obtient une évaluation de la moyenne cherchée. On peut également simuler cette expérience, à l'aide d'un langage de programmation. On effectue ensuite un grand nombre de fois (cent, puis mille) la procédure précédente et on fait la moyenne des résultats obtenus. On obtient des nombres oscillant autour de 33, qui est donc le nombre moyen d'achats nécessaires pour obtenir l'équipe complète (voir en encadré).
L'étude théorique est beaucoup plus subtile. Le nombre moyen de plaques à acheter est précisément de :
ce qui donne 33,2. L'expérience montre qu'il est plus rapide d'obtenir le résultat par simulation. L'intérêt de l'étude théorique réside dans la généralisation : on peut remplacer 11 par toute autre valeur et trouver que, pour n images, la valeur moyenne est égale à :
ce qui vaut environ n(ln n + g), où g = 0,577 à 10–3 près est la constante d'Euler. Ainsi, dans chaque cas, la simulation donne le résultat plus rapidement mais la démonstration l'explique mieux.
Lire la suite