Dans des régions tropicales ou subtropicales, certaines maladies sont transmises par des moustiques : c'est le cas notamment pour le paludisme, la fièvre jaune, la dengue, le chikungunya… Ce dernier a naguère défrayé la chronique à La Réunion ; il est provoqué par le moustique-tigre Aedes qui, quand il pique, transmet un virus par sa salive. La personne infectée devient fiévreuse, contracte des douleurs musculaires et des irritations de la peau, généralement pendant quelques jours, parfois pendant plusieurs mois. Il n'existe pas de traitement préventif contre cette infection, mais le corps d'un malade produit naturellement des anticorps, ce qui, généralement, lui permet de devenir immunisé, réfractaire à cette maladie.  Se pose alors la question d'évaluer, à court et à long terme, les effets réels d'une campagne de soins dans une région touchée par un tel fléau.

La détermination d'une matrice de transition

Considérons un pays dans lequel sévit une maladie qui se propage par des piqûres de moustiques. Sa population peut être répartie dans une (et une seule) des trois catégories suivantes : 

• l'ensemble, noté S, des individus sains, c'est-à-dire n'étant pas atteints par la maladie et n'étant pas immunisés ;

• l'ensemble I des personnes immunisées ;

• l'ensemble M des malades.

Les autorités sanitaires de cette contrée, qui relèvent chaque mois la répartition des habitants dans ces trois classes, ont observé qu'un individu a une probabilité constante de rester dans l'état dans lequel il se trouve ou bien de passer d'un état dans un autre. 

De façon plus précise, dans une période d'un mois :

• un individu sain ne peut pas devenir immunisé, mais a autant de chance de rester sain que d'attraper la maladie ; 

• une personne immunisée ne peut évidemment pas attraper la maladie ; elle a de fortes chances de rester immunisée, mais peut, avec une probabilité faible – égale à 10% pour fixer les idées – devenir saine (perdre son immunité) ;

• un malade ne deviendra pas sain, mais sera très probablement immunisé, la probabilité qu'il reste malade étant faible, par exemple 20 %.

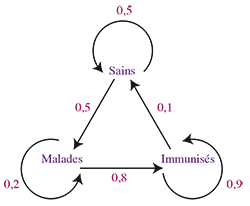
Ces données peuvent être visualisées par un graphe dont les sommets sont les trois catégories en question, tandis que les arcs traduisent la possibilité de passer d'un état dans un autre au cours de deux mois successifs, ces arcs étant munis d'une valeur égale à la probabilité correspondante.

Il est clair qu'une campagne de soins dans la région où sévit la maladie fera diminuer à court terme le nombre de malades. Mais, si la population n'a pas accès à un vaccin adéquat, la maladie continuera à se propager à cause de la présence persistante de moustiques. La question qui se pose concrètement consiste à savoir si une campagne de soins aura des effets durables.

Pour répondre à cette question, on peut exploiter une chaîne de Markov. Elle est définie par la matrice, qualifiée de transition, dont les lignes et les colonnes se réfèrent aux trois catégories de populations (dans l'ordre S, I, M) tandis que ses éléments de chaque ligne traduisent les probabilités de passer d'un état à un autre ; il s'agit de la matrice P suivante :

Markov, ses processus et ses chaînes

Le mathématicien russe Andreï Markov (1856–1922) a été l'élève de Tchebychev à l'Université de Saint-Pétersbourg, où il a enseigné. Après des premiers travaux sur des formes quadratiques, en théorie des nombres et en analyse (fractions continues, convergence de séries), il consacra ses recherches aux probabilités, et notamment aux processus stochastiques.Son nom désigne encore aujourd'hui un type de ces processus. 

Un processus de Markov se caractérise par une certaine absence de mémoire : la distribution conditionnelle de probabilité des états futurs ne dépend que de l'état présent et non des états passés.

Considérons une suite d'épreuves E₁, E₂, …, E_k,…dont les résultats possibles appartiennent tous à un ensemble fini {S₁,S₂,…,S_n} ; si le résultat de la k-ème épreuve est S_i, on dit que le système étudié se trouve dans l'état S_i à la k-ème transition (ou encore au temps k). 

On appelle chaîne de Markov une telle succession d'épreuves pour autant que la condition suivante soit satisfaite : pour tous indices i et j compris entre 1 et n, la probabilité que le système passe, lors d'une seule épreuve, de l'état S_i à l'état S_j ne varie pas au cours du temps : elle ne dépend donc pas des épreuves antérieures à E_k et est indépendante du numéro k de l'épreuve au cours de laquelle elle s'effectue. Pour tout couple d'états (S_i, S_j), on note p_ij la probabilité (constante) que S_j se produise immédiatement après S_i. Les nombres (p_ij) forment la matrice, appelée matrice de transition (ou de Markov) du processus stochastique considéré. Les puissances de la matrice P renseignent sur les probabilités de passer d'un état à un autre après plusieurs transitions.

L'encadré ci-contre montre l'évolution du cas de l'exemple de contamination vu plus haut, mois par mois, quand la matrice de transition est P, en partant d'une population également répartie entre S, I et M.

Compte tenu de l'existence d'une limite indépendante de l'état initial, on peut pronostiquer l'évolution de la maladie dans un futur lointain : quelle que soit la situation au début de l'étude,  il y aura, à très long terme (environ et de façon probabiliste) 15 % de la population analysée dans la catégorie S, 75 % dans I et (un peu moins de) 10 % dans M.

Concrètement, cela implique qu'une campagne de soins fait évidemment diminuer dans l'immédiat le nombre de malades, mais que ce dernier se stabilise pratiquement après un temps très long. Dès lors, si l'on veut éradiquer la maladie, une campagne de soins n'est pas suffisante : il faut travailler les facteurs qui génèrent la maladie. En d'autres termes, comme vu par ailleurs dans l'article de la page 32, il convient de modifier les éléments de la matrice P par une campagne de vaccination ou par l'élimination d'une quantité importante de moustiques.