Le paludisme, également appelé malaria, est une maladie connue depuis l'Antiquité qui tue encore de nos jours des centaines de milliers de personnes chaque année, principalement en Afrique. Alphonse Laveran, un médecin militaire français, découvre en 1880 en Algérie dans le sang de malades le parasite responsable de la maladie.

C'est en Inde en 1897 que Ronald Ross, un autre médecin militaire (britannique, cette fois), comprend que ce parasite est transmis à l'homme par la piqûre de moustiques du genre anophèle. Inversement, l'homme infecté peut transmettre le parasite à un moustique non infecté lorsque celui-ci le pique. Ce moustique ira infecter une autre personne et c'est comme cela que la maladie se propage dans une population. Ross reçoit le prix Nobel de physiologie ou médecine en 1902. Dans les années qui suivent, il met en place des campagnes de démoustication. En 1911, il propose un modèle mathématique pour expliquer qu'il n'est pas besoin de tuer les moustiques d'une localité jusqu'au dernier pour que le paludisme disparaisse. Il suffit d'en tuer suffisamment pour que la population de moustiques soit inférieure à un certain seuil.

Le notion de seuil pour éradiquer la maladie

Soit N la population humaine dans la localité et n le nombre de moustiques. Pour simplifier, on suppose que ces nombres restent constants au cours du temps. Soit I (t) le nombre d'humains infectés et i (t) le nombre de moustiques infectés au temps t. Cela veut dire que N – I (t) humains et n – i (t) moustiques ne sont pas infectés. Normalement, tous ces nombres devraient être des entiers positifs ou nuls. Mais on considère une population suffisamment grande pour que ces nombres apparaissent comme variant presque continûment. On obtient alors un système de deux équations différentielles couplées (voir encadré) qui exprime la variation, en fonction du temps, du nombre d'infectés : l'une pour 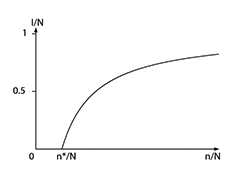les moustiques, l'autre pour les humains. Ross cherche les solutions stationnaires, c'est à dire constantes au cours du temps et il obtient le cas où la maladie est endémique, c'est-à-dire constamment présente dans la population ; celle-ci n'est envisageable que si le nombre de moustiques n est supérieur à un certain seuil noté n*. Il est possible de démontrer (ceci fut fait par Alfred Lotka en 1923) que si le nombre n de moustiques est inférieur au seuil n*, toutes les solutions du système convergent vers l'état d'équilibre sans maladie. En revanche, si n > n* et si la maladie est présente à t = 0, alors la solution converge vers l'équilibre endémique. Ainsi, Ross parvient bien à expliquer le phénomène curieux observé en 1911. 

Cette notion de seuil peut se comprendre de la manière suivante avec les notations de l'encadré ci-contre. Imaginons une population non infectée de N humains et n moustiques. Introduisons un moustique infecté. Celui-ci reste en vie en moyenne pendant une durée égale à 1 / m, car une mortalité constante signifie que la probabilité d'être encore vivant au bout d'un temps t est égale à exp (– mt). L'espérance de vie est alors égale à l'intégrale de exp (– mt) de 0 à l'infini, c'est-à-dire 1 / m. En moyenne, le moustique infecte donc f / m humains durant sa vie. Ces humains restent infectés pour une durée moyenne égale à 1 / g. Chacun reçoit en moyenne fn / N piqûres par unité de temps. Ils infectent donc fn / (gN) moustiques. Au bout d'un aller-retour entre les moustiques et les humains, on voit qu'un moustique infecté produit un nombre de moustiques infectés égal au produit (f / m) fn / (gN), c'est-à-dire f ² n / (gm N). 

Le paludisme ne peut envahir la population que si ce nombre, traditionnellement noté R₀ suivant la notation de Lotka, est supérieur à 1. On remarque alors que la condition R₀ > 1 est bien équivalente à n > n* (voir encadré).

Extensions et limites du modèle

Le modèle mathématique proposé par Ross a servi d'exemple pour de nombreux autres modèles développés depuis plus d'un siècle pour diverses maladies. Ross a notamment influencé son compatriote McKendrick, un autre médecin militaire, qui en 1927 en collaboration avec Kermack a proposé un modèle dit S-I-R pour les maladies transmises directement d'humain à humain (voir à ce sujet Tangente n°131 et l'article p. 28 de ce numéro). 

Les maladies transmises par des moustiques, telles le paludisme, la dengue ou le chikungunya, restent très présentes à travers le monde. Une épidémie de chikungunya a touché près d'un tiers de la population de l'île de la Réunion en 2005 et 2006. Des dizaines de milliers de cas ont également été signalés depuis 2014 en Guadeloupe, en Martinique et en Polynésie française. Même en France métropolitaine, le moustique-tigre Aedes albopictus colonise certaines régions, ce qui fait craindre de futures épidémies. Des modèles mathématiques sont développés pour essayer de prévoir et de mieux contrôler de telles épidémies. Il faut notamment prendre en compte les fluctuations saisonnières des populations de moustiques, les cas importés depuis d'autres pays et quantité d'autres paramètres qui font que la modélisation reste un exercice difficile.