Même si leurs prévisions sont forcément imparfaites, les modélisations mathématiques des épidémies sont destinées à aider la décision en politique de santé. Plus précisément, quand une maladie prend une allure épidémique, les modèles tentent de répondre aussitôt que possible à la question : est-on en présence du début d'une épidémie ? Si oui, quelle sera son ampleur ?

Le modèle SIR

William Kermack et Anderson McKendrick ont proposé la première modélisation réaliste en 1927. Leur modèle compartimente la population en trois classes : S, la classe des individus susceptibles d'attraper la maladie, I, celle de ceux qui en sont infectés (et contagieux) et R, ceux qui en sont revenus ou sont morts. Dans les deux cas, ces derniers sont immunisés et ne contamineront plus personne. Le modèle SIR suppose implicitement que la population totale (P = S + I + R) n'augmente pas et il considère l'évolution de ces trois classes dans le temps en fonction de deux taux mesurables expérimentalement. 

• Le premier (α) est le taux de contagion de la maladie pour un infecté, c'est-à-dire la probabilité qu'un individu susceptible attrape la maladie après contact avec un individu infecté, le nombre total de contacts étant censé être le produit IS (chaque infecté rencontre chaque personne susceptible de l'être). 

• Le second taux (β) mesure le passage de l'état I à l'état R. 

Après un laps de temps t, on compte donc α I S t infectés supplémentaires et R augmente de β I t. La variation du nombre d'infectés est donc égale à α S – β multiplié par I t. La condition pour que la maladie se propage (et donc donne lieu à une épidémie) est que le nombre de malades infectés augmente, c'est-à-dire que : α S – β > 0. Le quotient β / α a donc valeur de seuil. Si le nombre de sujets susceptibles est strictement inférieur à ce seuil, la maladie ne s'étend pas. Sinon, elle donne lieu à une épidémie (ou à une épizootie). 

D'une façon qui peut paraître paradoxale, l'apparition d'une épidémie ne dépend donc pas du nombre de personnes infectées mais du nombre de personnes susceptibles d'attraper la maladie ! Cette remarque justifie à elle seule les politiques de vaccination, même avec un vaccin peu efficace (voir le cas de la variole, en page 30). Pour éviter une épidémie, c'est le nombre d'individus susceptibles d'attraper la maladie qu'il faut diminuer ! 

C'est aussi le principe du théorème du moustique découvert par Ronald Ross en 1911, et selon lequel il n'est pas besoin d'éliminer tous les moustiques pour éradiquer le paludisme, il suffit d'en faire passer la population sous un certain seuil (voir l'encadré). Dans le cas de maladies comme Ebola où il n'existe pas de vaccin, il faut isoler les malades et protéger les soignants, ce que préconise effectivement l'OMS.

SIR en version continue

En général, on exprime ce seuil en fonction d'une notion issue de la démographie : le taux de reproduction de base R₀. En démographie, il s'agit du nombre moyen de filles par femme, notion qu'on peut étendre à chaque espèce d'animaux. De façon logique, si R₀ > 1, la population augmente, si R₀ < 1, elle diminue. Dans le cas présent, R₀ est le nombre d'infections causées en moyenne par un individu infecté au long de sa période infectieuse dans une population entièrement constituée de susceptibles (voir tableau ci-contre). Si S₀ est le nombre de susceptibles au départ (c'est-à-dire si S₀ = S (0)), la valeur de seuil pour S₀ étant égale à β / α, 

Taux de reproduction de base évalué pour les maladies infectieuses les plus courantes (dans l'ordre croissant des taux).

Si on reprend les calculs précédents en considérant un intervalle de temps infinitésimal dt, les augmentations de S, I et R sont : d S = –SI dt, d I = (αS – β) I dt et d R = β I dt.

Le modèle SIR se résume alors à un système différentiel qui permet de calculer le nombre I de personnes infectées dans sa population à chaque instant t :

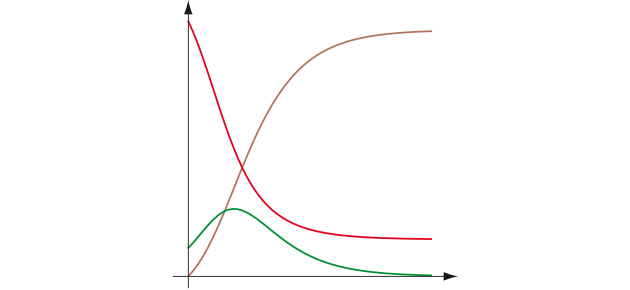
Il est impossible de trouver une solution exacte de ce système d'équations différentielles mais il est possible d'en déterminer des valeurs approchées en utilisant un logiciel de calcul, à partir des valeurs initiales de S, I et R, R₀ et β. Voici un exemple où les valeurs de départ de S, I et R sont respectivement 90 %, 10 % et 0, α = 2 et β = 0,9 donc R₀ = 2.

On remarque sur ce cas de figure qu'on arrive assez vite à un état d'équilibre où le nombre d'infectés s'éteint.

Le modèle SIR peut être amélioré en augmentant le nombre de compartiments. Il est par exemple courant d'introduire un état intermédiaire, E, pour exposés. On obtient le modèle SEIR correspondant à quatre équations différentielles à quatre inconnues. On peut également décomposer la population par âges, les taux de contagion n'étant pas les mêmes selon les âges. Il est enfin possible d'introduire une part de probabilités dans les passages d'un état à l'autre mais, sur les grands nombres, cela ne change pas fondamentalement le problème.

Les automates cellulaires pour simuler la propagation

Imaginons un damier infini, chaque case étant considérée comme une cellule qui peut être saine, infectée, morte ou immunisée. Au départ, toutes les cellules sont saines. On place une cellule infectée puis on applique itérativement la règle probabiliste suivante :

• les cellules voisines de la cellule infectée sont infectées au coup suivant avec la probabilité p ;

• la cellule meurt ou est immunisée le coup suivant.

Comment les cellules infectées (en rouge)  se multiplient-elles au détriment des cellules saines (en vert) ? Dans cet exemple, la probabilité qu'une cellule voisine d'une cellule infectée soit infectée à son tour est  de 25 %. Les cellules mortes ou immunisées sont représentées en bleu.

La question intéressante est : « Pour quelles valeurs de p, la maladie se propage-t-elle au monde entier ? ». Le modèle étant probabiliste, on ne peut donc prédire avec certitude ce qui va se produire dans un cas particulier. Pour avoir une idée rapide de l'évolution moyenne du système, le mieux est de procéder à des simulations. Pour cela, on itère l'application des règles énoncées ci-dessus en utilisant un générateur de nombres pseudo-aléatoires et on comptabilise le nombre de cellules infectées. En « jouant » cent fois de suite et en faisant la moyenne des résultats, on obtient une mesure de l'expansion moyenne de l'épidémie.

En dessous d'un certain taux de contamination p, l'épidémie ne s'étend pas. En revanche, au-dessus, elle envahit le monde entier. Dans le cadre de notre modèle simplifié, le taux critique se situe entre 30 % et 40 %. Une maladie ne devient épidémique que si ce taux est dépassé. Comment ce modèle peut-il être adapté à différents types d'épidémies ou d'épizooties ? 

Tout d'abord, on peut modifier le voisinage de chaque cellule (composé pour notre automate de huit cellules) : les spécialistes parlent de voisinage de Moore, du nom d'Edward Moore, l'un des fondateurs de la théorie des automates. Avec un voisinage plus simple, dit de von Neumann, constitué des quatre cellules partageant un côté avec la cellule considérée, le taux critique pour lequel la maladie devient épidémique se situe aux alentours de 60 %. 

On peut également améliorer le modèle en tenant compte du temps pendant lequel une cellule infectée est contagieuse puis du taux de mortalité et d'immunité ainsi que du temps d'immunité. On arrive ainsi à retrouver la façon dont se sont propagées des épidémies comme la peste dans l'Europe médiévale. Une première vague a tué le tiers de la population en se propageant à partir d'un épicentre situé dans un port, suivie de plusieurs répliques plus faibles, toutes partant du même point. Ces répliques correspondent à la fin de certaines immunités.

La confrontation avec les données épidémiologiques a permis de montrer que ce type de modèles a une certaine pertinence pour toutes les maladies qui se propagent par contact direct : grippe, tuberculose ou même sida. En revanche, il ne fonctionne plus lorsque la maladie se propage via un agent infectieux, comme dans le cas du paludisme ou du chikungunya.

L'usage des graphes  

Les graphes peuvent également être utiles dans la modélisation des épidémies. Imaginez une région où sévit une maladie se propageant par contact, dont la nature dépend du virus impliqué. Quand une personne rentre en contact avec une personne malade, elle devient malade avec une certaine probabilité, disons 5 % pour fixer les idées. 

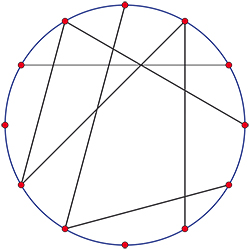Si les personnes sont les sommets et les contacts potentiellement contaminants les arêtes, cela donne un graphe.

L'ensemble des sommets restant fixe, l'évolution de l'épidémie se simule en tirant au sort chaque jour un certain pourcentage d'arêtes, disons 20 % pour fixer les idées. Le premier jour, on introduit un sommet infecté, qui contamine les sommets adjacents dans la journée avec une certaine probabilité. Puis on itère le procédé un certain nombre de fois, disons 100. Comme la question comprend une part aléatoire, on recommence un grand nombre de fois pour faire une moyenne. Ces simulations montrent à nouveau l'existence d'un seuil au-delà duquel l'épidémie se répand à la population entière, et en-deçà duquel, elle reste limitée.

Ce modèle est malgré tout imparfait. Certaines personnes ont plus de contacts avec les personnes infectées que d'autres : le personnel médical dans le cas de la grippe et d'Ebola, les personnes ayant de multiples partenaires sexuels dans le cas du sida. C'est vers eux que doit porter l'essentiel de la protection, pour éviter les contaminations.

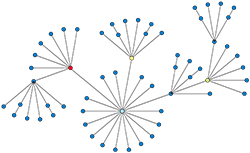
Pour conclure, on peut remarquer que ces divers modèles ne se contredisent pas : tous mettent un effet de seuil en évidence, même si chacun a son domaine d'application préférentiel. Les modèles compartimentaux comme SIR s'appliquent particulièrement bien à une population vivant dans un territoire homogène alors que les modèles utilisant des automates cellulaires ou des graphes seront plus adaptés à l'étude de la géographie d'une contamination. 

Enfin, il est également possible de combiner plusieurs modèles : par exemple, un modèle par automate cellulaire combiné avec un modèle de type SIR dans chaque cellule.