En sport d'équipes comme le football, le rugby, le handball ou le basket, la position des joueurs est commandée par des considérations géométriques. Christian Gourcuff, actuel entraîneur de l'équipe d'Algérie, très connu comme ancien entraîneur de Lorient, est aussi professeur de mathématiques. Sa conception du football s'en ressent comme on le voit dans cette interview qu'il donna à Libération en 1998 : 

« J'essaie de mettre en place une organisation géométrique du jeu. Elle passe par la maîtrise des espaces. On m'a reproché au début que ce système bridait la création. Je reste convaincu que l'organisation renforce en fait la créativité. Huit joueurs forment un bloc. Celui-ci se déplace en écran au porteur du ballon. L'idéal serait de maintenir des distances égales entre chaque joueur du bloc. On peut évaluer cette distance à environ 15 mètres. C'est un système assez rigoureux, qui comporte des risques. Si l'écart devient soudain trop important entre les joueurs, le réseau s'effiloche et l'organisation s'écroule. En revanche, si l'organisation reste intacte, les courses sont plus courtes et, par conséquent, la dépense d'énergie est moindre. C'est une organisation que l'on retrouve sous certains aspects dans le basket. »

Christian Gourcuff précise plus loin que ses joueurs sont placés sur deux lignes droites se déplaçant en diagonale vers le but adverse. Le plus difficile est de garder cette formation quand on recule. Bien entendu, il vaut mieux que le système ne soit pas trop rigide pour laisser place à l'utilisation des opportunités mais ce type de formation géométrique est une idée qui se retrouve dans tous les sports de ballons quand ils se jouent en équipe.

La géométrie de l'arbitre

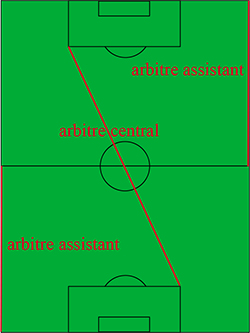
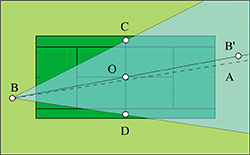
Les arbitres ont des problèmes de positionnement similaires. Pour optimiser leur vision collective du jeu, l'arbitre central se déplace en général selon une diagonale et ses assistants sur les lignes de touche opposées, comme sur la figure ci-contre.

Des questions mathématiques se posent à d'autres moments du jeu, comme celui de la remise en jeu après une touche. Quel est l'angle optimum pour que le ballon aille le plus loin possible ? Il n'est pas de 45° comme semblent le vouloir les lois de la balistique quand on les applique au tir au canon mais de 30° avec un effet dans le sens inverse des aiguilles d'une montre. Le résultat est sensiblement le même au lancer du poids où l'angle optimal est d'environ 35°. De même des problèmes d'angle se trouvent au moment du tir, ce qui est encore plus clair pour transformer un essai au rugby.

Transformer un essai

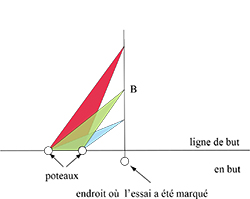
Au rugby, on marque un essai en écrasant le ballon dans l'en-but adverse, c'est-à-dire derrière la ligne joignant les poteaux. Pour transformer cet essai, le buteur doit poser le ballon sur la ligne passant par le point précis où l'essai a été marqué et perpendiculaire à la ligne de but, donc parallèle à la ligne de touche. Où placer le ballon sur cette ligne pour que la transformation soit la plus facile possible ?

Si l'essai a été marqué entre les poteaux, le problème est relativement simple à condition de se placer assez loin pour passer au-dessus de la barre transversale et se mettre à l'abri de la charge de l'équipe adverse. Tout change si l'essai a été marqué hors des poteaux. Déplaçons un point sur cette ligne. L'angle sous lequel on voit les buts depuis ce point augmente quand on s'éloigne de la ligne de but pour passer par un maximum, puis diminuer. C'est en ce point où l'angle est maximal qu'il convient de placer le ballon.

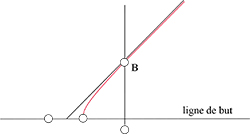
Quand nous faisons varier l'endroit E où l'essai a été marqué, le point M où l'angle est maximal décrit une courbe, qui se trouve être une hyperbole, ou plutôt un morceau d'hyperbole (voir l'encadré l'hyperbole de la transformation) :

Bien entendu, on imagine mal le buteur tracer une hyperbole sur le terrain pour transformer son essai. Comme le montre la figure ci-dessus, cette hyperbole se confond vite avec deux droites, ses asymptotes. Ce sont les droites passant par le centre des poteaux, inclinées de plus ou moins 45 degrés. Pour trouver le point idéal, le buteur se déplace donc, sur la ligne de transformation, de la distance séparant le milieu des poteaux au point de la ligne de but où l'essai a été transformé.

Comment se replacer au tennis ?

.

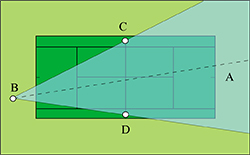
Un calcul plus savant permet d'évaluer l'erreur commise ainsi, et d'en tenir compte. Suivant la zone où se trouve celui qui doit renvoyer la balle, une correction est nécessaire. La figure de droite permet de visualiser l'erreur d'approximation : moins de 50 cm dans la partie claire jusqu'à plus de 2 m dans la foncée. Les courbes sur la figure sont des cercles de même axe : le filet.

Poursuivons l'étude de la géométrie des jeux de balles et de ballons en examinant les balles à effet. On obtient un effet en faisant tourner la balle sur elle-même. Ce phénomène a été étudié scientifiquement par Heinrich Magnus (1802 – 1870), c'est pourquoi on l'appelle l'effet Magnus.

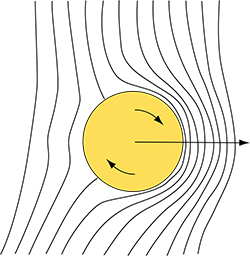De Platini à Roberto Carlos

En football, lors d'un coup franc, un tir brossé peut contourner le mur des défenseurs adverses pour revenir vers le but ! Fabien Barthez en sait quelque chose : le 3 juin 1997, lors du Tournoi de France, en match amical contre leBrésil, le gardien français ne réagit pas à l'obus tiré par Roberto Carlos sur coup franc. Le ballon, catapulté des trente mètres, contourne en effet complètement le mur de la défense, avant de revenir de manière spectaculaire dans le but (score final : 1–1). 

Cependant, l'effet dépend de la résistance de l'atmosphère. Lors du Mondial 1986, au Mexique, à 2 600 m d'altitude, Michel Platini a raté un pénalty décisif, sans doute parce qu'il n'avait pas tenu compte de cette différence…