Pour Schiller, « L'homme (...) n'est tout à fait homme que là où il joue ». Dès les jeux grecs, les compétitions sportives sont l'objet de paris. Les Romains perpétuent cette tradition, et les évergètes, précurseurs de Mécène, embauchent gladiateurs et auriges pour le plaisir du peuple. Contrairement aux jeux publics ou privés, les paris sportifs sont autorisés pour compléter le financement des athlètes.

Avec l'expansion du christianisme, il est reproché aux joueurs d'avoir recours à un usage illégitime de la providence divine et les jeux de hasard, et les paris sportifs deviennent donc clandestins. A partir du XVII^e siècle, l'assouplissement des positions de l'Église, les besoins de nouvelles finances pour l'État et la naissance de la théorie des probabilités, grâce à un joueur, le Chevalier de Méré, réhabilitent le jeu. Puis au XIX^e siècle, le jeu, péché censé encourager l'oisiveté, devient un vice, ce qui amène l'interdiction des jeux de hasard dans de nombreux pays, dont la France en 1836. Cette prohibition s'assouplit avec le temps : loi de 1907 sur les casinos, création du PMU en 1931 et rétablissement de la Loterie nationale en 1933. Le loto sportif, qui donnera le Loto Foot, apparaît en 1985.

La cote Foot

Le pari mutuel, inventé en 1865 par Michel Oller, parfumeur et premier bookmaker, consiste à mettre en commun les mises des joueurs, en prélever un pourcentage pour frais de gestion, et redistribuer la somme restante aux parieurs gagnants selon des cotes calculées en fonction des mises, sans aucun risque pour l'organisateur.

Pour les paris sportifs, un ensemble de données, statistiques et contextuelles, donnent pour chaque match des probabilités traduites en cotes. Le bookmaker applique alors sa marge, et équilibre les cotes. Les cotes proposées ne représentent donc pas les probabilités des évènements joués, mais sont le fruit d'un ajustement raisonné destiné à garantir le gain des bookmakers, seuls gagnants à long terme de ces paris.

Le Loto Foot consiste à parier sur les résultats d'une grille de matchs, classiquement 7 (LF7) ou 15 (LF15). Il s'agit de paris de type 1N2. Pour chaque match, le pari porte sur la victoire de l'équipe 1 ou 2, ou sur un match nul N.

Considérons le cas général d'un pari portant sur n jeux proposant p choix. Puisqu'il y a p choix par jeu, et n jeux, le nombre total de grilles à remplir, est N(n,p) = pⁿ. 

Ainsi, N(7,3) = 2187 grilles possibles pour le LF7, et N(15,3) = 14 348 907 pour le LF15. Si le risque d'une certitude peut être pris pour quelques matchs, le grand nombre de combinaisons restantes interdit de toutes les jouer. Une stratégie possible est d'accepter l'erreur, mais une seule, et de déterminer le nombre de grilles à remplir pour avoir la garantie de (n−1)  bons résultats. On parle de système « n – 1 » pour cette technique de réduction de nombre de grilles.

Si on appelle grilles « voisines » des grilles possédant n–1 jeux identiques, la grille solution possède alors n.(p–1) grilles voisines. Le nombre total d'éléments en voisinage est ainsi V(n,p) = 1+n.(p–1). L'idéal est donc de constituer un ensemble de voisinages distincts qui recouvre l'ensemble des grilles possibles. Une condition nécessaire pour un recouvrement optimal est que la quantité , représentant le nombre de grilles à remplir pour être certain d'avoir, au minimum, n–1 jeux gagnants, soit un nombre entier.

Nous allons transcrire cette condition sur le nombre n de jeux, en analysant simplement le cas où p est premier.

Puisque V divise une puissance de p premier, alors V = n.p – (n–1) doit être divisible par p et donc  n  1 mod p, c'est-à-dire n = 1 + α₁p. On a maintenant   et on continue par itération. Alors, en procédant de même, α₁   1 mod p, ou α₁ = 1 + α₂p et donc n = 1 + p + α₂p². 

En continuant de la sorte, on trouve pour condition que  .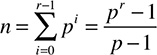

On vérifie alors que pour  et  , on a V(n,p) = p^r et donc R = p^n-r. Il resterait à démontrer qu'il s'agit là d'une condition suffisante. On peut, à défaut, illustrer cette condition sur deux exemples.

Du tennis au foot, quelques exemples

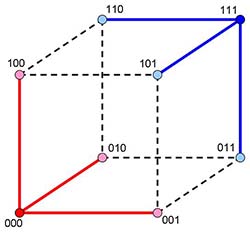Pour des matchs de tennis, p = 2 (pas de match nul), et les nombres de parties permettant une réduction optimale du nombre de grilles sont de la forme n =2^r – 1, soit n = 3,7,15,31,... Dans ce cas, V(r,2) = 2^r et R = 2^n-r. Ainsi, pour trois parties (r=2), R=2 grilles suffisent, parmi les N=8 possibles, pour avoir la garantie de deux parties gagnantes. On peut illustrer ce résultat par un graphe, vite illisible avec un grand nombre de parties, dont les sommets, les grilles, sont reliés entre eux par une arête s'ils sont voisins. Notre problème est alors de trouver deux sommets tels qu'en coloriant leur voisinage tous les sommets soient colorés, et une seule fois. Pour N = 8 sommets, ayant chacun V – 1 = 3 voisins, ce graphe est un cube. On vérifie (voir figure 1) qu'en sélectionnant deux sommets diagonalement opposés, aucun sommet ne reste incolore (isolé).

En notant les p = 2 résultats d'un match par 0 ou 1, le résultat d'une grille est constitué de trois digits, et l'ensemble des huit jeux possibles correspond ainsi à la notation binaire des chiffres de 0 à 7. Dans l'exemple, chacune des directions du cube est associée à un digit, et les coordonnées cartésiennes des sommets du cube d'arête unité correspondent aux grilles à jouer.

Pour le Loto Foot, p = 3, et les valeurs du nombre de parties qui permettent une réduction 

« n – 1 » optimale sont de la forme

soit 1,4,13,40 etc. Alors, V(r,3) = 1 + 2.n =3^r et R = 3^n-r. Pour r =2, nous avons n = 4 jeux, N =81 grilles possibles et R = 9 grilles suffisent pour une réduction « n – 1 ». 

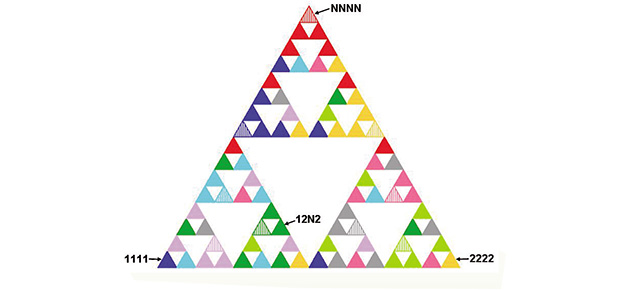
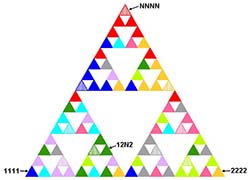La figure 2 illustre ce cas de façon originale avec la fractale de Sierpinski d'ordre 4. Les sommets d'un triangle élémentaire représentent les trois choix d'un match, 1 pour le sommet à gauche, N pour le sommet central et 2 pour celui de droite. Pour expliquer la correspondance sommet-grille, prenons le sommet correspondant à la grille 12N2 de la figure 2. Au premier ordre, la fractale est constituée de trois triangles. Le sommet se trouve dans celui de gauche, d'où le 1 du premier jeu. Dans ce triangle, il se situe dans le plus grand triangle de droite (2 pour le jeu suivant), à l'échelle suivante, il appartient au triangle du milieu (N), et enfin, au dernier niveau de la structure, il est à droite (jeu 2), d'où sa correspondance avec la grille 12N2. Les neuf grilles à jouer pour un recouvrement optimal sont les sommets hachurés, leurs voisins étant colorés en plein de la même couleur.

Pour le LF3, cinq grilles permettent une réduction « n – 1 » alors que R = 3,86. 

Pour le LF7, R =145,8 et l'optimum est actuellement de 186 grilles. Déterminer un algorithme général de détermination de grilles pour résoudre le système « n – 1 » reste un problème ouvert !