Les cubiques du triangle

Depuis Descartes, il est devenu usuel de caractériser un point du plan euclidien par ses deux coordonnées dans un repère arbitraire. Mais pour une étude analytique des propriétés du triangle, il est choquant, pour le géomètre guidé par d’efficaces principes esthétiques, de rompre la symétrie intrinsèque en choisissant un sommet pour origine ou un côté pour vecteur de base. L’expression d’un résultat se doit d’être invariante par toute permutation des sommets du triangle. Trois coordonnées doivent alors être mises en jeu, mais reliées par une relation (puisque le problème est plan, donc de dimension 2). C’est le principe des coordonnées trilinéaires et des coordonnées barycentriques, qui seront ici utilisées pour déterminer des points et courbes remarquables du triangle.

[encadre]

Les coordonnées barycentriques

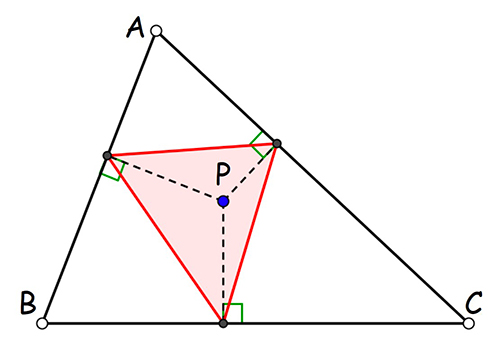
Pour un triangle ABC, d’aire ∆_ABC , dire que le point P admet le triplet (x : y : z) pour coordonnées barycentriques signifie qu’il est le barycentre des masses x en A, y en B et z en C, tout en remarquant que des masses proportionnelles ont le même barycentre.

Notons respectivement S_X = ∆_PBC , S_Y = ∆_PAC et S_Z = ∆_PAB les aires des triangles PBC, APC et ABP. Par construction, le point X est le barycentre de ( B, y) et (C,z) et donc  \( \dfrac{\overline{\text{XC}}}{\overline{\text{BX}}} = \dfrac{y}{z}.\)

La surface de triangles de même hauteur étant proportionnelle à leur base, on a  \( \dfrac{y}{z} = \dfrac{\Delta_{\text{XAC}}}{\Delta_{\text{XAB}}}= \dfrac{\Delta_{\text{XPC}}}{\Delta_{\text{XPB}}},\)

et donc  \( \dfrac{y}{z} = \dfrac{\Delta_{\text{XAC}} - \Delta_{\text{XPC}}}{\Delta_{\text{XAB}} - \Delta_{\text{XPB}}} = \dfrac{\text{S}_{\text{Y}}}{\text{S}_{\text{Z}}}.\)

Il en est de même pour les autres côtés. Les coordonnées de P sont donc (x : y : z), mais aussi ( S _X : S _Y : S _Z). Les masses qui définissent, au sens des coordonnées barycentriques, un point P du plan sont proportionnelles aux aires des triangles que P définit avec les sommets A, B et C. Le point peut être extérieur au triangle ABC si l’on prend des aires orientées.

[/encadre]

Les coordonnées triangulaires

Pour tout point P du plan défini par les points A, B et C non alignés, les trois vecteurs  \( \overrightarrow{\text{PA}}, \overrightarrow{\text{PB}}\) et  \( \overrightarrow{\text{PC}},\) sont dépendants, donc liés par une relation de la forme  \( \alpha \overrightarrow{\text{PA}} + \beta \overrightarrow{\text{PB}} + \gamma \overrightarrow{\text{PC}} = \overrightarrow{{0}}.\)

Alors le point P est dit barycentre des points (A, B, C), respectivement affectés des coefficients (α, β, γ). Pour indiquer que le barycentre est invariant en remplaçant (α, β, γ) par des valeurs proportionnelles ( μα, μβ, μγ), on notera indifféremment P ( μα : μβ : μγ) ou P (α : β : γ).
Ceci justifie la dénomination de coordonnées homogènes par Möbius en 1827. En effet, on appelle fonction homogène de degré p une fonction  f de n variables telle que
f ( λ x₁, λ x₂… λ x_n) = λ ^p f ( x₁, x₂… x_n) pour tout réel λ, et les coordonnées barycentriques sont homogènes de degré 0 puisque ( λα : λβ : λγ) = λ⁰(α : β : γ).

Dans ce système de coordonnées, les sommets du triangle sont A(1 : 0 : 0), B(0 : 1 : 0) et C(0 : 0 : 1). Les céviennes, droites passant par l’un des sommets, associées au point
P(x : y : z) interceptent les côtés du triangle aux points X(0 : y : z), Y(x : 0 : z) et Z(x : y : 0). Ceci signifie simplement que le point X, par exemple, est le barycentre des points B et C avec les coefficients y et z. On a donc  \( y \cdot \overline{\text{XB}} + z \cdot \overline{\text{XC}} = 0,\) soit  \( \dfrac{\overline{\text{XC}}}{\overline{\text{XB}}} = -\dfrac{y}{z},\) où \( \overline{\text{XC}}\)  est la mesure orientée du segment [XC].

Une autre façon de déterminer avec unicité la position d’un point P du plan est de considérer ses distances (u, v, w) aux trois côtés du triangle. Notons P(u, v, w) ces nouvelles coordonnées, dites trilinéaires. Il nous reste à établir une relation entre ces deux systèmes de coordonnées triangulaires. En notant S = 2∆_ABC le double de la surface du triangle ABC, on a au = 2S_X, bv = 2S_Y, cw = 2S_Z et, par suite, au + bv + cw = S.

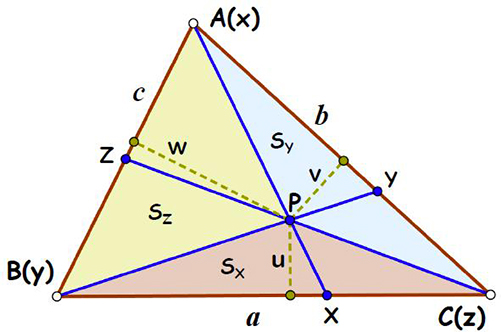
Les coordonnées triangulaires.

D’un système à l’autre

Comment passer d’un système de coordonnées à l’autre ?

Puisque P (x : y : z) a aussi pour coordonnées barycentriques (S_X : S_Y : S_Z), on peut aussi écrire, grâce au calcul précédent, P ( au : bv : cw). On en déduit P (u, v, w), les coordonnées trilinéaires de P. Et pour un point P de coordonnées barycentriques (x : y : z), ses coordonnées trilinéaires sont  \( \text{S} \left( \dfrac{x}{a}, \dfrac{y}{b}, \dfrac{z}{c} \right)\) si x + y + z = 1.

Pour exemple, le centre de gravité G est le barycentre des sommets du triangle affectés du même coefficient de pondération : G(1 : 1 : 1). Le centre I du cercle inscrit de rayon r est, par définition, à la distance r de chaque côté du triangle. Ses coordonnées trilinéaires sont (r, r, r), et, par suite, (a : b : c) sont ses coordonnées barycentriques. Par définition de ces coordonnées, on en déduit immédiatement qu’une bissectrice partage le côté opposé dans le rapport des côtés adjacents. 

On définit en coordonnées barycentriques le « produit » commutatif P₁ • P₂ des points
P₁ ( x₁ : y₁ : z₁) et P₂ (x₂ : y₂ : z₂) par P₁ • P₂  (x₁ x₂ : y₁ y₂ : z₁ z₂) : les coordonnées du produit sont les produits des coordonnées. L’élément neutre de ce produit, tel que P • G = P pour tout point P, est le centre de gravité G. Tout point P (x : y : z) tel que xyz ≠ 0, donc n’appartenant à aucun côté, admet un inverse P ⁻¹ pour ce produit : P ^-1( x ⁻¹ : y ⁻¹ : z ⁻¹). On vient de définir une loi de groupe sur l’ensemble du plan (privé du périmètre) grâce à laquelle on peut construire le produit, le carré, la racine carrée de points du plan.

Intéressons-nous maintenant aux transformations naturellement liées au triangle. De façon générale, une isoconjugaison φ est une transformation des points du plan involutive, donc telle que φ ² (P) = P pour tout point P. La connaissance d’un point P et de son conjugué P* =φ (P), pourvu qu’ils soient différents et pas situés sur le périmètre du triangle, suffit pour construire l’isoconjugué M* de tout point M. En définissant le pôle d’une isoconjugaison comme l’isoconjugué Ω = G* ( p : q : r ) du centre de gravité, l’isoconjugaison de pôle Ω est la correspondance : \( \text{M}(x : y : z) \mapsto \varphi _{\Omega} (\text{M}) = \text{M}^* \left( \dfrac{p}{x} : \dfrac{q}{y} : \dfrac{r}{z} \right),\)  ce qui s’écrit, avec les notations du produit, M • M* = Ω. Un point J invariant par isoconjugaison est donc tel que J² = Ω .

Tout point du plan P est à l’intersection de trois droites issues des sommets du triangle, les céviennes, qui coupent les côtés opposés aux points P_A, P_B et P_C. Les symétriques de ces points par rapport au milieu de leur côté sont les points Q_A, Q _B et Q _C, eux-mêmes traces des céviennes d’un point Q. Par construction, la transformation qui associe Q à P est involutive, puisqu’une symétrie l’est. Elle est appelée conjugaison isotomique (« même coupe ») et notée t. Puisque le point G est manifestement invariant par cette conjugaison, il en est aussi le pôle puisque G ² = G. Cette transformation fait donc correspondre au point P (x : y : z) son inverse pour le produit, le point Q = tP = (x ⁻¹ : y ⁻¹ : z⁻¹).

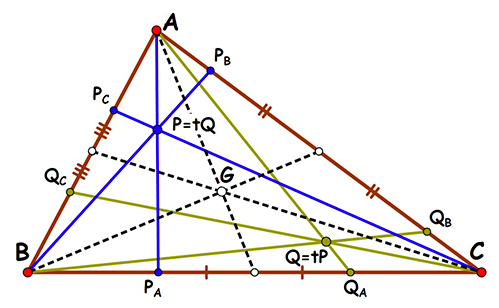
La conjugaison isotomique. 

Pour la conjugaison isogonale (« même angle »), notée g, les céviennes de deux points conjugués sont, cette fois-ci, symétriques par rapport aux bissectrices, d’où le nom de cette transformation involutive. Le centre du cercle inscrit I(a : b : c) étant invariant par cette conjugaison, le pôle est le point de Lemoine K = I², qui est le point de rencontre des symédianes, symétriques des médianes par rapport aux bissectrices. De la relation générale P • gP = K, on déduit que la conjugaison isogonale fait correspondre au point P (x : y : z) le point  \( g\text{P}= \left( \dfrac{a^2}{x} : \dfrac{b^2}{y} : \dfrac{c^2}{z} \right)\)  puisque K a pour coordonnées barycentiques (a ² : b ² : c ²).

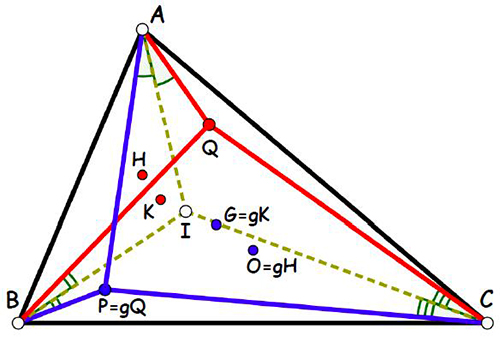
La conjugaison isogonale.

Ces isoconjugaisons permettent de déterminer les coordonnées barycentriques de nombreux points caractéristiques associés à la géométrie du triangle, appelés centres (voir encadré).

[encadre]

Les centres du triangle

On appelle fonction centrale une fonction homogène f des longueurs a,
b et c des côtés d’un triangle, qui est en plus symétrique par rapport à b
et c ; autrement dit f (a, b, c) = f (a, c, b). Pour un centre (ou point remarquable) X dont les coordonnées s’obtiennent les unes des autres par permutation
circulaire des valeurs (a, b, c), on écrit : X = [  f (a, b, c)] pour X = (  f  (a, b, c) : f (b, c, a) : f (c, a, b)). L’Encyclopédie des centres de triangles (ETC) est un inventaire en ligne de plus de trente-six mille de ces points. Elle en comptait dix fois moins il y a dix ans !

[/encadre]

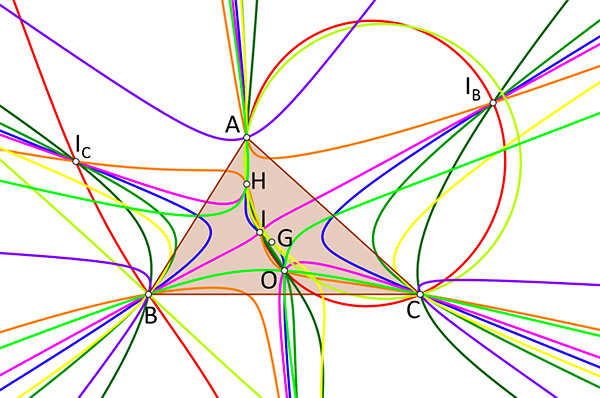
Les isocubiques à pivot

Trois points définissent avec unicité un cercle, cinq, une conique et il en faut neuf pour une cubique, courbe du troisième degré. Le site « Cubics in the triangle plane » de Bernard Gibert recense plus de mille cubiques remarquables construites sur les centres du triangle. Limitons-nous ici aux isocubiques à pivot pK(Ω, P) de pôle Ω et de pivot P. Ce sont des courbes telles que chacun de ses points Q et son Ω-conjugué Q* sont alignés avec le pivot P. On en déduit que la tangente au point pivot P passe par son conjugué P*. Pour P (u : v : w) et Ω = ( p : q : r ), l’équation de la cubique pK(Ω,P) est
ux (ry ² − qz ²) + vy ( pz ² − rx ²)+wz ( qx ² − py ²) = 0. Elle passe par les sommets du triangle, et les tangentes en ces points concourent au conjugué P* de P, de coordonnées barycentriques  \( \left( \dfrac{p}{u} : \dfrac{q}{v} : \dfrac{r}{w} \right).\)

La cubique de Lucas pK( X₂, X₆₉ ) est la cubique isotomique K007 de pôle X ₂ = G et de pivot X₆₉ le conjugué isotomique de l’orthocentre H, soit X₆₉ = tH = [ b ² + c ² − a ² ]. La tangente en ce point pivot passe donc par l’orthocentre. C’est, entre autres propriétés, le lieu des points P dont le triangle cévien est un triangle podaire. Le point de Bevan X₆₉ = Be de la figure est le symétrique du centre I du cercle inscrit par rapport au centre O du cercle circonscrit à ABC.

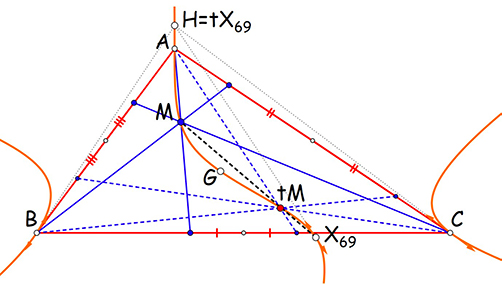
K007 (la cubique de Lucas).

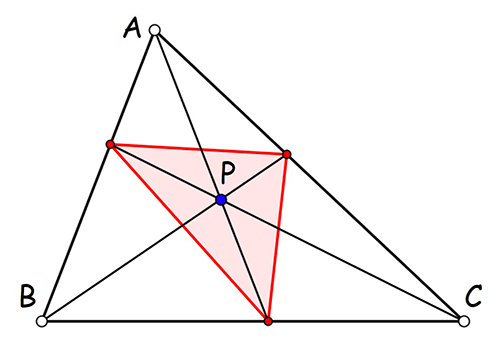
Triangle cévien.

Triangle podaire.

La cubique de Darboux pK( X₆ , X₂₀ ) est la cubique isogonale K004 dont le pôle est le point de Lemoine X₆ = K et le pivot le point de Longchamps X₂₀ = L. C’est, entre autres propriétés, le lieu des points P dont le triangle podaire est un triangle cévien.

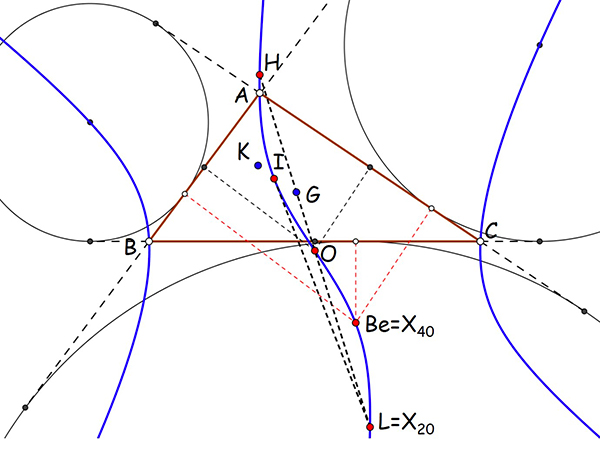
K004 (la cubique de Darboux).

On peut établir une bijection entre ces deux cubiques, en considérant que le triangle cévien d’un point M de la cubique de Lucas est le triangle podaire d’un point P de la cubique de Darboux. L’orthocentre H appartient à ces deux cubiques puisque ses céviennes sont les hauteurs, et donc son triangle cévien est identique à son triangle podaire.

De même, le centre de gravité, dont les céviennes interceptent les côtés en leur milieu, est associé au centre du cercle circonscrit O, point d’intersection des médiatrices, perpendiculaires aux côtés en leur milieu. Et au centre du cercle inscrit I correspond, par définition, le point de Gergonne.

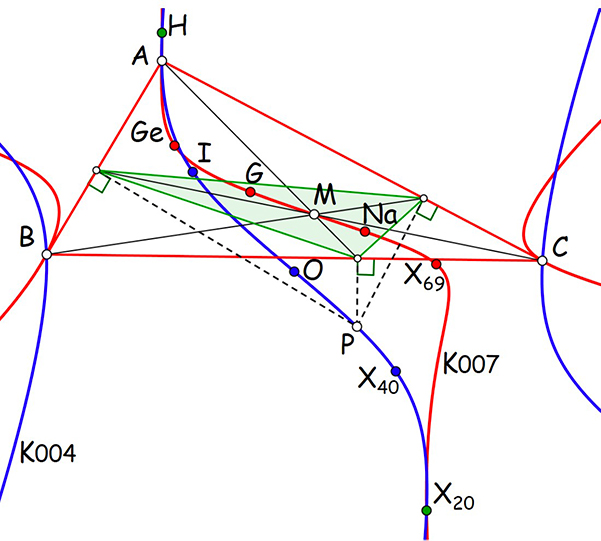
Correspondance cubique de Darboux - cubique de Lucas.

Une structure de groupe peut être définie sur K004, tout comme sur K007 (voir « Les courbes elliptiques »). La somme M + N de deux points M et N est alors le conjugué isogonal du troisième point d’intersection Q de la cubique avec la droite (MN). L’élément neutre de cette addition est alors le pivot X₂₀ =L, et donc les points Q, Q* = M + N et L sont alignés, par définition des cubiques à pivot.

Que le triangle, par sa nature, mène à la notion de cubique est encore illustré par une miniature liée au théorème de Siebeck, auteur en 1858 du terme « isogonal » (voir encadré). Tous ces exemples ne sont qu’un minuscule échantillon des propriétés attachées au choix de trois points quelconques du plan. Ouvrez la porte des sites de Clark Kimberling et Bernard Gibert pour découvrir la jungle des centres et cubiques des triangles !

Les dix premières cubiques, K001 à K010 (voir aussi Tangente 179, 2017, page 2).

[encadre]

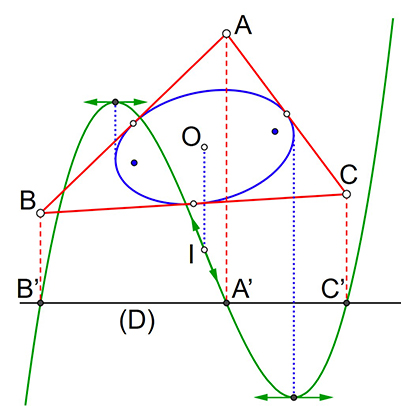
L’ellipse dérive du triangle

Le théorème de Siebeck, attribué à tort à Marden, considère, dans le plan complexe, le polynôme du troisième degré qui s’annule aux sommets A, B et C d’un triangle. Alors son polynôme dérivé, du second degré, s’annule aux foyers de l’ellipse de plus grande surface interne au triangle, l’ellipse de Steiner (S), tangente en leurs milieux aux côtés du triangle (voir les Nombres complexes, Bibliothèque Tangente 63, 2018). Voilà qui est remarquable !

Projetons maintenant, dans le plan euclidien, les sommets du triangle sur une droite D des abscisses quelconque, et traçons la cubique y = P(x), avec P polynôme de degré trois, qui passe par ces projetés. On montre alors que, quelle que soit la droite choisie, les droites perpendiculaires à D passant par les extrema de la cubique (c’est-à-dire vérifiant P′(x) = 0) sont tangentes à l’ellipse (S). De plus, le point d’inflexion I (tel que
P′′(x) = 0) et le centre O de (S) ont la même abscisse sur D. Ces propriétés confortent le lien différentiel entre un triangle et son ellipse de Steiner !

[/encadre]