
La fin du XIXe siècle fut le témoin d’une véritable contre-révolution artistique, née de la contestation de la production en masse de piètre qualité et de l’industrialisation à outrance. Elle trouva sa source en Grande-Bretagne. En Angleterre en effet on vit se développer le mouvement Arts and Crafts (« arts et artisanats ») dès 1860, un mouvement qui visait à réhabiliter la production des artisans, redécouvrant le travail à la main. L’idéologie qui sous-tendait ce retour aux sources s’étendit en Europe, donnant naissance, tout au long de la dernière décennie du siècle, à l’Art nouveau en Belgique, en France et en Tchécoslovaquie, au Jugendstil en Allemagne et en Autriche, allant même jusqu’à inspirer le mouvement Mingei au Japon.
Détruire les barrières
On connaît généralement bien les réalisations de tous ces mouvements en matière d’architecture (voir Mathématiques et architecture, Bibliothèque Tangente 60, 2017) mais la revalorisation du travail de l’ouvrier se fit dans tous les domaines et l’Art nouveau devint un art total, détruisant la barrière existant jusqu’alors entre arts « majeurs » et arts « mineurs » et entendant offrir à chacun un univers esthétique idéal même dans le plus petit objet utilitaire. Il engloba donc aussi bien la peinture, la sculpture et l’architecture que l’ébénisterie, la production de couverts, de lampes, de bijoux, de verreries. En privilégiant les courbes et les arabesques, il prôna la redécouverte de la nature (faune et flore), multipliant également les représentations féminines.

Les arts : danse.
Le recours systématique aux courbes est particulièrement visible dans la production très caractéristique du peintre tchèque Alfons Mucha (1860–1939), qui fit une grande partie de sa carrière en France, élevant l’affiche au rang de véritable œuvre d’art. Ainsi peut-on observer, dans les Arts : danse, le choix systématique de l’artiste de l’usage de cercles et d’ellipses, alternant avec de véritables hyperboles, faisant ainsi l’apologie des formes bilinéaires. On l’observe, le buste de la jeune femme est habilement mis en valeur par un encadrement de deux cercles contenant une théorie de cercles aux rayons de plus en plus petits. Mais ce n’est pas tout : chaque mèche de l’opulente chevelure affecte la forme d’une ellipse et le drapé de l’ample écharpe translucide est constitué d’une suite de paraboles. Plus généralement, chez Mucha, chaque visage féminin prend le plus souvent la forme d’une ellipse parfaite.

Par opposition, les représentations masculines sont fort rares dans l’œuvre du peintre tchèque. Elles n’apparaissent que comme pendant à de gracieuses et séduisantes demoiselles et se révèlent volontairement anguleuses, refusant d’être cadrées par une ellipse, comme on peut le constater dans cette publicité pour les biscuits Lefèvre-Utile (à l’origine de l’acronyme LU), accolant les initiales de ses deux fondateurs, Jean-Romain Lefèvre et Pauline Utile.

Le recours à la courbe se retrouve également dans le mobilier, et c’est plus étonnant, le caractère utile des meubles étant plus compatible avec la droite qu’avec le cercle. Qu’importe ! Les ébénistes trouvèrent la parade en multipliant les éléments décoratifs courbes, sans affecter le caractère utilitaire de l’objet.
De la courbe à la droite
Cercles, ellipses et paraboles sont donc toujours bien présents. Mais certains créateurs allèrent plus loin. Ainsi, le génial céramiste, maître verrier et ébéniste Émile Gallé (1846–1904) n’hésita pas à user des points d’inflexion, s’intéressant ainsi (sans le savoir ?) à des courbes d’allure « proche » des cubiques ou de polynômes de degré supérieur. Dans l’image suivante, une rotation de 90° fait apparaître de tels exemples. Gallé déplora toujours ses faiblesses en mathématiques qui l’empêchaient, disait-il, d’être un véritable scientifique. Il se concentra donc sur la biologie et principalement sur la botanique, publiant notamment plusieurs articles sur la variabilité des végétaux, étudiant les mutations de la gentiane et de certaines orchidées. Sa production verrière aux élégants décors floraux reste très prisée aujourd’hui. Elle allie les formes aux courbures élégantes, assorties de points d’inflexion, aux représentations idéalisées de la nature.

Comment ne pas voir d’élégantes courbes mathématiques derrières ces productions de René Lalique ?

Deux vases « Art nouveau » (de style École de Nancy) signés Émile Gallé.
L’omniprésence de la courbe laissa également des traces en bijouterie. Le mathématicien Cédric Villani a conquis un public très large en parlant de triangles gras et de triangles maigres (voir le coffret de quatre DVD « Un mathématicien aux Métallos », Shim Sham Films, 2017). Le bijoutier et maître verrier René Jules Lalique (1860–1945) en a usé des décennies plus tôt en y intégrant des animaux stylisés, pour le plus grand bonheur des dames, quand il ne s’inspire pas ouvertement de la lemniscate (voir encadré), sans doute pour mieux faire étalage du caractère infini de son inspiration.
[encadre]
La lemniscate
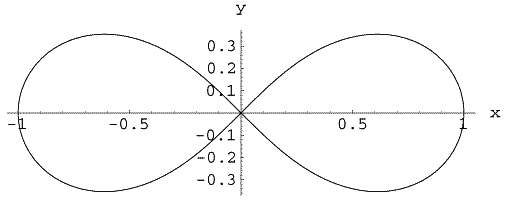
Le symbole représentant l’infini n’est pas issu de la lemniscate de Bernoulli (à savoir Jakob Bernoulli, 1654–1705), puisqu’il fut introduit par le mathématicien britannique John Wallis (1616–1703), un précurseur de Newton. Il faut bien avouer cependant que la courbe considérée a des allures bien proches du symbole en question. Une lemniscate (particulière) de Bernoulli se définit en coordonnées polaires par l’équation r2 = cos (2u), u parcourant le domaine [0, π / 4] < [3π / 4, π].
[/encadre]
La Première Guerre mondiale signa la fin du mouvement Art nouveau, qui fit la place, dès la fin des hostilités, à l’Art déco, premier art total mondial. La droite reprenait le pouvoir. Mais qu’est une droite si ce n’est une courbe bien particulière, de courbure nulle ?
Lire la suite