Éoliennes : modélisation et simulations des écoulements d'air

Lorsqu’on regarde une éolienne tourner, rien ne laisse penser que l’air autour d’elle est à la fois ordonné et chaotique. Il est d’abord ordonné car les pales en rotation de l’éolienne induisent un sillage (il s’agit de la modification de l’écoulement due à la présence d’un obstacle). Ce sillage provoque un ralentissement de l’air et génère des tourbillons. Ces derniers sont générés à la racine et en bout de pale, à cause de la rencontre de la dépression d’un côté de la pale et de la surpression de l’autre.

Des maths dans le vent

Les tourbillons générés s’enroulent de façon hélicoïdale en aval du rotor à cause de la rotation des pales. Lorsque la vitesse de rotation est faible, ils restent stables longtemps et sont transportés sur de très longues distances. Si la vitesse augmente, les tourbillons commencent à interagir, à s’apparier, et finissent par se déstabiliser et se mélanger. Plus la vitesse est grande, plus vite et plus violente apparaît cette déstabilisation. À vitesse élevée, le « mélange de spaghettis arc-en-ciel », comme sur l’image du haut, représente en fait des tourbillons d’air de différentes tailles, formes et vitesses. C’est pourquoi on dit aussi que l’air est chaotique. Pour caractériser la « quantité de chaos », on utilise le nombre de Reynolds (voir FOCUS). Pour l’écoulement autour d’éoliennes dans l’atmosphère, le nombre de Reynolds peut dépasser dix millions ! À cette valeur, l’écoulement est donc très fortement turbulent.

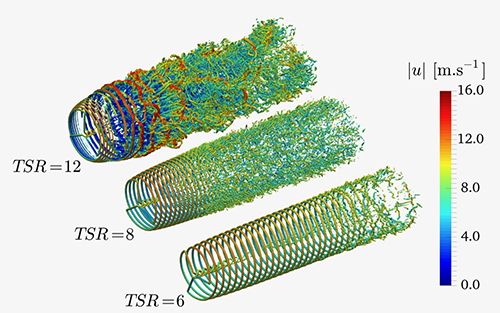
Visualisation des tourbillons dans le sillage d’éoliennes à différentes vitesses de rotation, sans turbulence en amont ; les couleurs sont fonction de la vitesse.

D’un point de vue pratique, les éoliennes sont souvent regroupées dans un parc éolien. Plusieurs rotors sont alors alignés, comme s’ils suivaient une grille, avec un espacement entre éoliennes de quelques fois leur diamètre. Cette proximité implique que le sillage généré par une turbine va avoir un impact sur une autre éolienne placée en aval de l’écoulement. C’est l’interaction des sillages. Le vent « vu » par la deuxième éolienne est alors différent du vent amont : la vitesse moyenne est plus faible et ses fluctuations, dues à la turbulence, plus importantes. Ces effets de sillages sont uniquement observables dans de rares conditions d’humidité où le sillage devient identifiable grâce à un brouillard qu’il produit lui-même.

Vue aérienne du champ éolien en mer Horns Rev II (photo prise par Bel Air Aviation Denmark-Helicopter Services le 26 juillet 2016).

Comme les sillages provoquent une diminution de la vitesse moyenne, l’énergie du vent arrivant sur les éoliennes en aval est plus faible. Leur production électrique s’en trouve donc diminuée, ce qui est dommageable. Les fluctuations de vitesses dans le sillage sont elles aussi un problème car elles provoquent des efforts plus importants sur la structure des pales et de la tour de l’éolienne.

Pour toutes ces raisons, il est important de comprendre et de prédire les écoulements autour des éoliennes. Un des outils utilisés est la simulation numérique, qui consiste à résoudre par ordinateur les équations de la mécanique des fluides : les incontournables équations de Navier–Stokes.

La Normandie, comme chaque région, est équipée d’un supercalculateur. Ainsi, le méso-centre CRIANN, à Rouen, héberge MYRIA, qui permet aux chercheurs et entreprises d’accéder à des architectures techniques spécialisées et d’effectuer des simulations de grande taille, tant du point de vue du nombre de processeurs, de la mémoire disponible que du temps de calcul. La Maison normande des sciences du numérique (MNSN), en lien avec le CRIANN, consolide un écosystème normand du calcul intensif (HPC), de la simulation numérique avancée et de l’ingénierie des données numériques.

Bien implanter sa ferme

Afin de rendre compréhensibles des équations physiques continues par un ordinateur, il est nécessaire de modifier ces équations. C’est l’étape de discrétisation : les équations de Navier–Stokes sont réécrites sur des volumes élémentaires (des cubes d’un centimètre de côté par exemple) du domaine fluide étudié. Le volume autour d’un champ éolien peut faire plusieurs kilomètres cubes !

Le nombre N de volumes élémentaires dépend directement du nombre  Re de Reynolds : N est de l’ordre de grandeur de Re^9/4. Il faudrait donc environ deux cents volumes élémentaires pour Re = 10, cinq millions pour Re = 1 000 et cinq millions de milliards pour les écoulements autours des éoliennes avec Re = 10⁷. On comprend pourquoi on utilise des supercalculateurs.

Les chercheurs et ingénieurs développent en permanence des solutions pour réussir de tels calculs. La plus utilisée consiste à résoudre uniquement les « plus grands » tourbillons de l’écoulement. Le besoin en volumes élémentaires s’en trouve drastiquement réduit. Afin que les calculs restent justes, il faut prendre en compte l’effet des « petits » tourbillons sur les plus grands. C’est la modélisation : on prédit mathématiquement le phénomène physique. Avec cette méthode, on peut prédire l’écoulement autour d’éoliennes.

La modélisation d’un champ de vent réaliste à partir de données ponctuelles issues de M stations météo (ou anémomètres) est un problème crucial afin d’optimiser le lieu et l’installation d’une ferme d’éoliennes. L’objectif est de réaliser l’approximation d’un champ de vecteurs à partir d’un ensemble de données ponctuelles de la forme (x_i , y_i , U_i , V_i )_1≤i≤M où (x_i , y_i )_1≤i≤M désigne la localisation de la station météo numéro i et où les (U_i , V_i )_1≤i≤M sont les composantes du vecteur vitesse et la direction du vent au point considéré. Les données sont donc la « valeur » du champ du vent en un nombre fini M de points.

Le point de départ de la modélisation de ce problème est la supposition que le champ de vecteur « dérive d’un potentiel » (pour le cas du vent, qui nous concerne, la température convient). L’objectif final est d’obtenir une approximation globale de l’ensemble du champ de vecteurs sur un domaine d’étude Ω borné (par souci de simplification).

En outre, contrairement aux méthodes d’interpolation, on préfère une méthode de lissage pour approcher les données (c’est notamment utile lorsque le nombre de vecteurs est très grand ou lorsque les données sont bruitées, ce qui est assez courant). Cependant, si on l’estime nécessaire, il sera aussi possible de faire de l’interpolation, c’est-à-dire de « passer » exactement par les données.

De la modélisation mathématique à la simulation numérique

Le cœur de la modélisation est la minimisation d’une fonctionnelle d’énergie J qui rassemble un terme de « fidélité aux données », \( \langle\rho\nu-w\rangle\) , et un « critère de lissage » \( \varepsilon |\nu|_{m+1,\Omega}\)  : on définit alors  \( J(\nu)=\langle\rho(\nabla\nu )-w\rangle ^2_{M}+\varepsilon |\nu |^2_{m+1,\Omega}\)  où < > désigne la norme euclidienne et w représente l’ensemble des données du champ de vent et où   \( |\cdot |_{m+1,\Omega}\)
désigne la semi-norme de l’espace de Sobolev H^m+1(Ω). Les espaces de Sobolev fournissent des critères de régularité des dérivées partielles des fonctions considérées.

Le problème de la minimisation de J peut être considéré comme étant de type régularisation des moindres carrés sur un espace bien adapté. L’existence et l’unicité d’une solution à ce problème continu, théorique sont obtenues via des outils mathématiques classiques en théorie des équations aux dérivées partielles et en approximation.

Afin d’implémenter cette méthode, on discrétise le domaine d’étude via un maillage. Une méthode de discrétisation (la méthode des éléments finis) permet ensuite d’approcher la solution du problème de minimisation ci-dessus, qui aura été préalablement transformé en problème variationnel. La solution approchée est obtenue dans une base polynomiale, les coefficients de cette solution approchée sont des réels qui sont déterminés via la résolution d’un système linéaire.
Des résultats de convergence montrent que la solution ainsi approchée converge vers la solution du problème continu théorique lorsque l’on maille le domaine d’étude de plus en plus finement. Ces méthodes d’approximation sont d’une grande utilité pour faire des simulations d’une ferme d’éoliennes : grâce à des données réelles, une connaissance de la topographie de la zone d’étude et une implémentation robuste et parallélisée, il devient possible de réaliser des simulations précises, et donc de contribuer à définir une potentielle production d’énergie optimale.

Des enjeux sociétaux européens

Des approches mathématiques rigoureuses alliées à des algorithmes sophistiqués permettent ainsi de répondre à de nombreux défis proposés par le secteur de l’énergie, notamment l’énergie éolienne (avec Engie Green et Siemens-Gamesa, dans le cadre de projets soutenus par la région Normandie et l’Europe avec en particulier les laboratoires Coria et LMI). De nombreux autres aspects mathématiques faisant intervenir équations aux dérivées partielles, analyse numérique, optimisation, probabilités et statistiques sont mobilisés dans des applications liées à l’énergie : problèmes inverses et imagerie sismique pour rendre visible l’invisible (le sous-sol) en ingénierie pétrolière ; statistiques pour définir le productible éolien ; approximation de la houle par des fonctions splines afin de simuler des hydroliennes… Autant de défis mêlant des laboratoires de recherche académiques et des partenaires industriels. Les aspects de simulation numérique sont également au cœur de ces enjeux scientifiques et sociétaux, les méso-centres de calcul, les maisons du numérique (cf. le réseau MSO), permettent ainsi de contribuer à l’obtention de résultats réalistes à partir de grands volumes de données.

Les trois auteurs exercent à l'INSA Rouen Normandie. Pierre Bénard comme maître de conférences (Labo. CORIA), Eugénie Gourichon (ingénieure en mathématiques) comme directrice de la recherche, Christian Gout comme professeur (Labo. LMI).