Des matrices et des graphes en comptabilité

Les mathématiciens professionnels de la Renaissance, les mathematici, incluaient la comptabilité dans leur enseignement. Aujourd’hui, les utilisateurs de comptabilité utilisent les quatre opérations arithmétiques de base, essentiellement l’addition ou la soustraction, parfois la division ou la multiplication, pour calculer des coûts ou des ratios. S’il leur arrive parfois de manipuler exponentielles ou logarithmes pour les calculs d’actualisation, ils ne vont guère au-delà. Pour autant, des techniques mathématiques de plus en plus sophistiquées peuvent être exploitées.

La comptabilité en partie double

L’enregistrement des mouvements de chaque compte (client ou fournisseur) est caractérisé par deux composantes : le montant des débits   \( (\Sigma\mathrm{E}_y)\)   et le montant des crédits  \( (\Sigma\mathrm{R}_y)\) ,  E qualifiant les emplois et R les ressources. On peut ainsi représenter le compte par un couple ordonné de nombres  \( \mathrm{C}_y=(\Sigma\mathrm{E}_y,\Sigma\mathrm{R}_y)\) , où \( \mathrm{C}_y\in\mathbb{R}^+\times\mathbb{R}^+\) . On est en présence d’un espace vectoriel à deux dimensions.

Dans l’histoire de la comptabilité, on a utilisé quatre formes d’écriture : les pictogrammes, les signes-mots, les signes syllabiques et les alphabets.

À tous les âges, et dans tous les pays, on a également utilisé un nombre limité de types de comptes. À côté des comptes à postes superposés (comptes sumériens, comptes égyptiens), il existe des comptes à colonnes séparées, où l’on consacre une page de registre ou de document pour les variations positives (entrées ou recettes ou emplois ou débits), par exemple la page de gauche et la page d’en face (celle de droite) pour les variations négatives (sorties, dépenses, ressources ou crédits). Le troisième type de présentation des comptes est le tracé à colonnes mariées, comme sur nos relevés bancaires aujourd’hui, où, sur la même feuille, les augmentations et les diminutions occupent deux colonnes voisines. Le quatrième type est la comptabilité matricielle, la dernière à avoir été introduite.

La consolidation

La consolidation des comptes a longtemps été une spécialité anglo-saxonne. En France, elle n’est devenue obligatoire que depuis 1985, mais elle existait depuis 1968. Elle permet d’établir les états financiers d’un groupe de sociétés contrôlées par une holding pour qu’ils soient publiés, mais aussi pour être utilisés à des fins internes au groupe. Elle permet d’agréger (c’est-à-dire d’additionner) les comptes de chaque société en un ensemble unique. Cette agrégation, sous forme classique ou sous forme matricielle, ne cause pas de vrai souci.

Ce qui pose problème, c’est l’obligation d’éliminer les opérations réciproques et d’effectuer des retraitements pour rendre les additions possibles (d’une part), et l’obligation de déterminer la nature et le pourcentage réel de contrôle et de participation d’une société-mère dans ses filiales, en particulier lorsque le contrôle n’est pas direct ou lorsque le contrôle est réciproque (d’autre part). Dans tous ces cas, la comptabilité matricielle permet d’apporter des solutions rationnelles.

Le problème de la consolidation est un cas particulier de théorie des graphes, où non seulement il est nécessaire de valoriser les arêtes, comme dans le cas général, mais encore de valoriser les sommets.

Pour mesurer la difficulté, traitons un cas simple, celui où un groupe est composé d’une société holding et d’une seule filiale. Une société-mère SM possède X % du capital de sa filiale FU, qui possède elle-même Y % du capital de sa société holding. Si la filiale possède Y % de sa société-mère, les autres actionnaires de la société-mère possèdent (100 – Y) % de leur société. Ils détiennent donc [(100 – Y) %] × X % de la filiale. Mais, comme les participations sont réciproques, on est en présence d’une « boucle infinie », qui est associée à une somme de termes en progression géométrique dont la somme est :
[(100 – Y) × X] × [(100 – Xⁿ Yⁿ) / (100 – XY)], qui tend vers [(100 – Y) × X] / (100 – XY) lorsque n tend vers l’infini. Au-delà de deux filiales, il devient vite impossible de faire des calculs simples à partir de fractions, et on doit utiliser des techniques plus sophistiquées (voir FOCUS).

Lorsque la complexité des groupes augmente, les participations croisées et circulaires sont difficiles à déceler d’un simple coup d’œil. Devant cette sophistication croissante, les responsables et les auditeurs doivent surveiller les phénomènes d’opacité et de dilution des actifs dans les nombreuses filiales. Seules les techniques matricielles sont capables de faire ressortir la réalité cachée sous des apparences plus ou moins trompeuses.

Polyèdres réguliers et graphes

Lorsqu’on est amené à faire un audit, dans le cadre d’une mission légale de commissariat aux comptes, on peut être frappé par une sorte de « désordre architectural » des groupes, constitués au hasard en fonction des opportunités d’achat ou de contrôle. Souvent, lorsque le groupe est déséquilibré, pour quelque raison que ce soit, il n’est pas facile de lui redonner une structure harmonieuse.

En s’inspirant de l’architecture des solides de Platon, totalement symétriques, on peut obtenir des structures très cohérentes, plus résistantes aux pressions extérieures et plus faciles à contrôler, permettant une meilleure circulation de l’information et des produits.

En faisant abstraction des faces et en réduisant les solides aux arêtes et aux sommets, on peut les représenter par des graphes. Pour construire un groupe à consolider avec de tels objets topologiques, il faut d’abord choisir la situation de la société-mère, par exemple au centre du graphe, et décider d’une participation majoritaire dans les principales filiales. Ensuite, il faut que chaque sommet ne reçoive pas plus de 100 % des contrôles et que lui-même n’en exerce pas plus de 100 %.

Prenons par exemple le cas du tétraèdre : on peut essayer de voir ce que donnerait une structure où la société-mère contrôlerait 90 % de ses trois filiales directement, et 5 % indirectement, ou encore 50 % directement et 45 % indirectement, ou enfin le cas où toutes les sociétés se contrôleraient mutuellement à hauteur de 10 %. Une fois qu’on a choisi la structure, on est ramené au problème précédent : calcul des participations du groupe, calcul des participations hors groupe et détermination des participations réelles de la société-mère dans chacune de ses filiales.

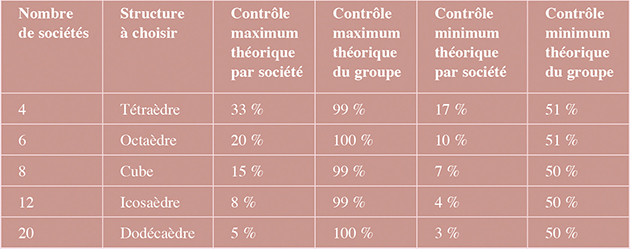
On peut aussi essayer de déterminer les limites de l’autocontrôle pour chaque type de graphe : le tableau donne quelques indications. Mais alors l’autocontrôle du groupe sur lui-même serait absolu, ce qu’il faut éviter car il empêcherait les actionnaires (personnes physiques du groupe) de voter. Autrement dit, la meilleure organisation comptable peut également être la plus étanche vis-à-vis de l’extérieur.

Des solutions concrètes et performantes aux problèmes de management

Il existe encore beaucoup de problèmes comptables, liés aux groupes de sociétés, où les matrices et les chaînes de Markov sont utiles : calcul des capitaux propres, calcul des réserves et des résultats du bilan consolidé de la société holding, optimisation de la trésorerie du groupe, planification des projets d’investissement du groupe… en utilisant la méthode des options réelles probabilisées et risquées associées aux chaînes de Markov, simulations et prévisions à court, moyen et long terme. Les méthodes matricielles apportent à la comptabilité complexe non seulement une indispensable rigueur scientifique, mais aussi une créativité porteuse de valeur ajoutée, le formalisme des mathématiques étant une garantie de rigueur et de contrôle. De plus, présentée dans les formes développées ici, la comptabilité a une meilleure aptitude à servir de base au calcul économique et à ses spéculations, à soutenir et à valider les éléments quantitatifs éclairant une stratégie.

La comptabilité, en elle-même, n’a pas toujours vocation à lier des paramètres autrement que par calcul. L’économie peut, au contraire, mettre en lumière les éléments positifs ou contradictoires d’un problème, avec toutes les nuances et tous les prolongements nécessaires. Mathématiques, économie et comptabilité sont souvent dissociées dans la recherche et dans l’enseignement, mais il est parfois utile de les réintégrer pour apporter des solutions concrètes et performantes aux problèmes de management.

Cet article est rédigé à partir de textes de Jean-Guy Degos publiés dans La Revue du FINANCIER.
Jean-Guy Degos, décédé en 2017, était professeur en sciences de gestion à l’université de Bordeaux. Titulaire de trois doctorats, il avait exercé comme expert-comptable et commissaire aux comptes. Il est l’auteur de 24 livres, de 28 e-books et de 170 articles, écrits ou traduits en huit langues.