
Disponible en ligne à l’adresse suivante https://automathon.univ-lille.fr et développé en 2019 par Julien Gheysens, Yvan Stroppa et les auteurs de cet article au sein de la jeune pousse MATHILDE, ChickenPods s’inscrit dans la droite lignée de l’incontournable Agar.io (Matheus Valadares, 2015) ou du jeu de plateau Quoridor (Gigamic, 1997) pour la simplicité de ses règles – une partie suffit pour comprendre ! – tout en garantissant une grande marge de progression.
Chaque joueur dispose de six minutes pour faire prospérer sa population de poules. Et tant mieux si c’est au détriment de l’adversaire ! En plus du mode 1vs1 actuellement proposé, une IA (un mode « contre l’ordinateur ») sera bientôt disponible. La principale difficulté de ChickenPods est que le joueur ne contrôle pas le déplacement de ses propres poules et agit seulement sur leur environnement (on parle de jeu de simulation divine ou God game) au moyen de quatre pouvoirs : la construction et la destruction de barrières, l’ajout de nourriture (des graines), et l’envoi d’un renard pour décimer le camp adverse.

Générer des environnements aléatoires
La partie débute avec un nouvel environnement proposé aux deux joueurs : des régions riches en graines qu’il serait judicieux de conquérir au plus vite, et un labyrinthe de barrières qui sont autant d’obstacles pour y accéder. Pour combattre la répétitivité du jeu et générer des environnements (et donc des parties) différents, les concepteurs utilisent le hasard. Mais un hasard contrôlé ! Il s’agit de produire des environnements « suffisamment originaux » pour ne pas lasser le joueur, c’est le rôle du hasard, mais répondant néanmoins à un certain cahier des charges pour donner lieu à une partie « intéressante ». En ce sens, ChickenPods est un jeu de génération aléatoire.

En début de partie, plusieurs zones riches en graines sont situées dans l’aire de jeu. Elles sont destinées à être conquises par les poules pour agir comme des relais stratégiques dans leur développement. Ces zones disposées aléatoirement doivent d’une part être à distance respectable les unes des autres et d’autre part bien couvrir l’aire de jeu. C’est ici qu’interviennent les k-DPP. Ces processus bien connus en théorie des probabilités (voir encadré) permettent de jeter des points au hasard dans le plan – ce sont nos zones de nourriture – sans être « trop proches les uns des autres ». On parle de répulsion entre les points.
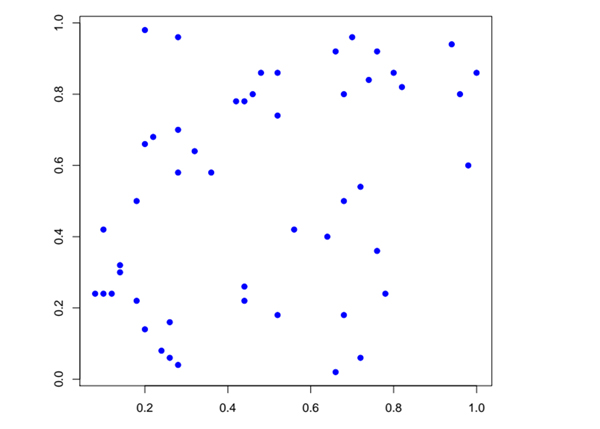
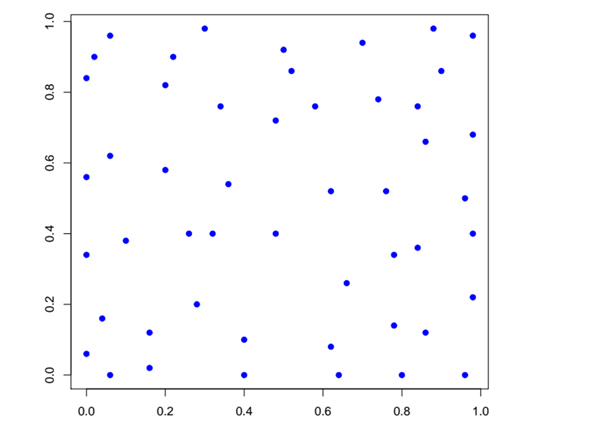
Pour s’en rendre compte, rien de tel qu’une mise en situation. Examinons deux simulations de k points jetés au hasard, sans interaction dans celle du haut, avec interaction répulsive dans celle du bas. En haut, les k points sont jetés indépendamment et uniformément dans le carré, ce qui produit naturellement des régions « très denses » et d’autres « complètement désertes ». À l’inverse, en bas, le k-DPP tend à repousser les points les uns des autres et donc à « bien occuper » toute la zone.
Un labyrinthe de barrières
La partie débute dans une aire de jeu totalement fissurée par de nombreuses barrières, créant ainsi un véritable labyrinthe aléatoire, qui possède cependant la propriété de pouvoir rallier chaque zone de nourriture sans avoir à détruire de barrières. Aux joueurs de décider de leurs propres stratégies : aller tout droit à la façon d’un bulldozer (ce qui nécessitera de détruire des barrières), ou laisser ses poules errer dans les méandres du labyrinthe. Dans ChickenPods, cette propriété est encodée par l’utilisation de chemins auto-évitants générés aléatoirement. Ce sont des serpentins formés de petits segments de longueur 1, horizontaux ou verticaux, qui ne reviennent jamais sur eux-mêmes (voir Mathématiques discrètes et Combinatoire, Bibliothèque Tangente 39, 2010). C’est cette dernière caractéristique qui garantit au labyrinthe de ne pas contenir de cycle.
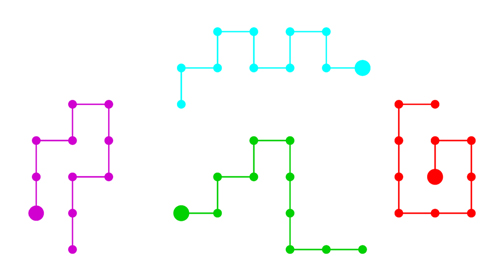
Quatre chemins auto-évitants de longueur 10.
Bien qu’étant des objets combinatoires tout à fait élémentaires, les chemins auto-évitants lancent aux mathématiciens de redoutables défis. Par exemple, il n’existe pas de formule générale donnant le nombre c (n) de chemins auto-évitants de longueur donnée n. Il n’existe à ce jour pas d’autre solution que de les compter un par un ! Et pour cela, l’utilisation d’un ordinateur est fortement conseillée : sur un réseau carré, on recense par exemple c (10) = 44 100 chemins auto-évitants de longueur 10, et c (71) = 4 190 893 020 903 935 054 619 120 005 916 chemins auto-évitants de longueur 71, qui est la plus grande valeur de c (n) connue précisément aujourd’hui.
On ne sait pas non plus choisir avec équiprobabilité un chemin auto-évitant de longueur n, parmi tous ceux de même longueur, « de manière efficace », lorsque n est « grand ».
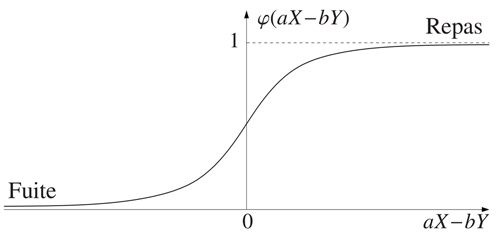
La fonction d’activation.
Des poules intelligentes plutôt que des lapins crétins !
Dans ChickenPods, chaque poule est mue par un réseau de neurones indépendant de ceux des autres gallinacés, la guidant dans ses actions toutes les deux secondes (voir Intelligence artificielle, Bibliothèque Tangente 68, 2019). Chaque réseau de neurones utilise des informations propres à la poule (ce sont les neurones d’entrée ou inputs rouges) : son état de santé (a-t-elle faim ou non ?), sa vision du terrain (y a-t-il des poules amies ou ennemies au voisinage, des barrières ou des graines ?) et une mémoire de ses actions passées.
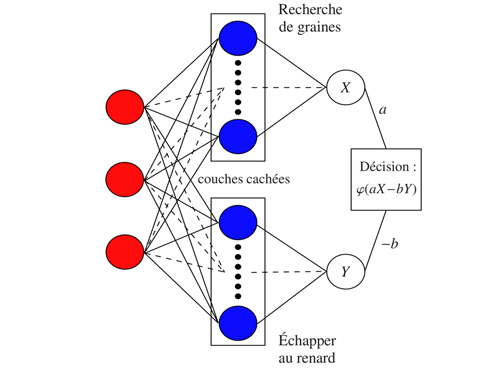
Le réseau de neurones d’une poule.
Le schéma ci-dessus montre comment le réseau de neurones d’une poule combine ces informations locales pour produire deux quantités X et Y décrivant deux états qui peuvent être simultanément incompatibles : X pour la propension de la poule à s’alimenter et Y pour celle à échapper au renard. Si le terme aX l’emporte devant bY, alors la poule décidera de picorer plutôt que de s’enfuir. Plus exactement, c’est la valeur de la fonction d’activation φ prise en aX – bY qui indique la probabilité avec laquelle la poule s’alimente ou non.
Alors, êtes-vous plutôt « poules intelligentes » ou « lapins crétins » ?

David Coupier est enseignant-chercheur à l’Université polytechnique Hauts-de-France (UPHF) et responsable du GDR GeoSto, groupement de recherche en géométrie aléatoire.
Nicolas Wicker est enseignant-chercheur à l’université de Lille.
Lire la suite