
De nouvelles technologies bouleversent notre quotidien à un rythme accéléré. La préservation de l’environnement dans une perspective de développement durable requiert une anticipation à moyen et long terme de l’impact des actions qui sont menées. De multiples facteurs politiques, économiques et sociaux conditionnent l’avenir.
Pour toute entreprise, pouvoir anticiper le changement devient une condition de survie. Les modèles numériques permettent à présent de décrire l’évolution de systèmes complexes qui dépendent de nombreux paramètres. Ils présentent toutefois des limitations, qui font de la prospective un art autant qu’une science.
Prévoir l’évolution d’un système
L’extrapolation des données suivant la tendance observée reste largement pratiquée pour prévoir une évolution future. Ainsi, comme la croissance de la consommation d’énergie se poursuit actuellement au rythme de 2 % par an, la prévision de la consommation d’énergie ou d’autres ressources est le plus souvent basée sur une loi exponentielle. En pratique, les ressources sont finies et leur consommation ne peut croître indéfiniment.
Dans le cas du pétrole, en se basant sur le rythme de progression actuel de la consommation, on arriverait à un quasi doublement d’ici 2050, alors que beaucoup d’experts estiment que l’on a atteint d’ores et déjà un plateau de production, aux environs de 95 Mb / j (millions de barils par jour). Un tel plafonnement de la production peut être représenté par une courbe sigmoïde Y, dont la relation en fonction du temps t s’écrit Y(t) = K / (1 + a exp(–rt)) pour a, r des constantes positives adéquates. Cette fonction est la solution de l’équation différentielle du modèle de Verhulst, qui l’avait qualifiée de fonction logistique :
où K > 0.
La fonction Y converge vers un plateau de niveau K.
De façon surprenante, ce comportement n’est plus observé lorsque l’équation différentielle est transposée sous la forme discrète suivante : xn +1 = µ xn (1 – xn ), avec x0 compris entre 0 et 1. La suite logistique (xn )n ≥ 0 ainsi obtenue ne converge que pour µ ≤ 3. Au-dessus de cette valeur, elle oscille, et, au-delà de µ = 3,57, elle devient « chaotique ».
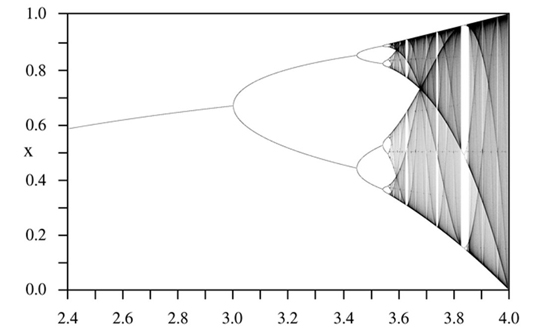
L’ensemble des valeurs prises par la suite logistique en fonction de la valeur de µ.
Le comportement « chaotique » est caractérisé par une multitude d’évolutions possibles, qui peuvent varier de façon considérable en fonction de la valeur initiale. Ainsi, ayant représenté l’atmosphère par un jeu simplifié d’équations, le météorologue Edward Lorenz a montré que la dynamique de l’atmosphère est très sensible aux conditions initiales. Une petite perturbation, en un point donné, peut entraîner des phénomènes météorologiques de grande ampleur ; c’est ce qui a été qualifié d’effet papillon. En outre, un tel système évolue vers un attracteur qualifié d’étrange par David Ruelle, formé dans l’espace des phases par un ensemble fractal de points dont la dimension est non entière. Le comportement du système garde une forme d’ordre, mais son évolution devient imprévisible.
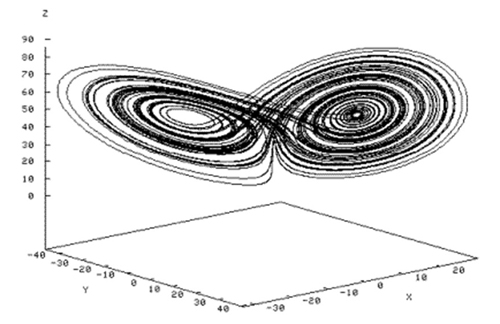
L’attracteur de Lorenz comporte deux points fixes instables.
Fluctuations et aléas
L’exemple du comportement turbulent d’un fluide au-delà d’une certaine vitesse d’écoulement, qui illustre une évolution vers le chaos, explique l’intermittence de l’éolien. En l’absence de mécanismes de régulation adéquats, un tel comportement chaotique peut être également observé dans bien d’autres domaines tels que les cours en bourse ou les prix des matières premières.
Tous les phénomènes imprévisibles ne sont pas toutefois le résultat d’un « chaos déterministe ». De nombreux phénomènes peuvent être considérés comme purement aléatoires. C’est le cas des fluctuations boursières, assimilables à un « bruit de fond » : elles peuvent être décrites comme un processus brownien suivant une chaîne de Markov aléatoire. Benoît Mandelbrot (1924–2010, voir les Fractales, Bibliothèque Tangente 18, 2019) a analysé ces fluctuations sous forme de distributions fractales, ouvrant ainsi un vaste champ à la recherche dans le domaine des mathématiques financières.
Les modèles stochastiques les plus usuels (en particulier le modèle de Black et Scholes) sur lesquels s’appuient les options financières, destinées à protéger leurs acquéreurs des aléas de la bourse ainsi que nombreux produits dérivés, font le plus souvent appel à des distributions gaussiennes. Mais ces modèles tendent à sous-estimer l’impact d’évènements peu fréquents dont les conséquences sont considérables, comme par exemple une crise au niveau mondial (voir Mathématiques et Finance, Bibliothèque Tangente 32, 2019). Ce sont les fameux « cygnes noirs ».
La dérégulation de l’économie dans le cadre de la globalisation a rendu le monde plus incertain. Cette situation a inspiré des méthodes de gestion « au bord du chaos » (voir le Chaos management, Tom Peters, Dunod, 1998). Toutes les entreprises sont concernées, mais les méthodes de gestion à employer diffèrent bien entendu selon leur nature. Alors qu’une start-up du numérique peut prospérer « dans le chaos », au jour le jour, des entreprises qui investissement sur le long terme, comme les compagnies énergétiques, doivent privilégier les moyens visant à renforcer leur résilience.
Le chaos nécessite un « mode d’emploi » (voir Chaos mode d’emploi, solutions individuelles et collectives, Bruno Marion, Yves Michel, 2014). Il s’agit tout à la fois de s’en protéger et de l’exploiter pour innover. On le constate d’ailleurs : les organisations dynamiques et vivantes doivent constamment naviguer entre ordre et chaos.
La méthode des scénarios
La plupart des situations « à grande échelle » (impliquant de multiples facteurs) ne se conforment pas à un modèle déterministe. De ce fait, la prospective a abandonné l’idée de prédire l’avenir et se contente de prévoir différents avenirs possibles, les futuribles selon l’expression de l’écrivain et économiste Bertrand de Jouvenel.
Afin de pouvoir aborder un avenir qui demeure incertain, on fait appel à la méthode des scénarios, qui permet d’envisager plusieurs futurs possibles. C’est en particulier la méthode suivie par le Groupement d’experts intergouvernemental sur l’évolution du climat (GIEC) pour envisager différents futurs climatiques possibles, suivant l’évolution des émissions de gaz à effet de serre. L’élaboration d’un scénario nécessite un horizon temporel : à court terme (quelques années), à moyen terme (dix à vingt ans) ou à long terme (au-delà). Bien entendu, plus l’avenir est lointain, plus l’incertitude augmente.
Dans le cas d’une entreprise, il est fréquent d’établir des scénarios en fonction de la conjoncture économique, qui peut être supposée se maintenir, s’améliorer ou se dégrader. Dans un contexte de développement durable, il est possible également d’inclure dans l’élaboration des scénarios un critère environnemental.

Scénarios PIB / environnement.
On obtient ainsi quatre scénarios de base : croissance du PIB et croissance des émissions de gaz à effet de serre (scénario BAU pour « business as usual ») ; croissance du PIB et diminution des émissions (scénario technologique, en supposant que le progrès technologique permettra de régler les problèmes environnementaux, sans sacrifier la croissance du PIB) ; décroissance simultanée du PIB et des émissions (scénario de décroissance) ; décroissance du PIB et croissance des émissions (scénario de crise économique, cette dernière étant elle-même reliée à la crise écologique). Chaque scénario fait le plus souvent l’objet d’un modèle numérique, qui permet de chiffrer les conditions de fonctionnement du système considéré.
Les scénarios peuvent être exploités de différentes façons. Il est possible d’affecter à chacun un niveau de probabilité. Il est également possible de considérer le scénario « le plus pessimiste » pour se prémunir contre toute éventualité. On peut enfin définir un scénario « souhaitable » et étudier tous les moyens pour le favoriser.

IA et Big Data : pas de solution miracle !
La méthode des scénarios doit toutefois être suivie avec prudence car certains scénarios normatifs, définis à partir de conditions fixées d’avance, peuvent s’avérer impossibles à atteindre. En outre, les scénarios doivent rester cohérents et ne pas reposer sur des hypothèses qui se contredisent (comme une maximisation à court terme du profit d’un côté et la préservation d’un développement durable d’un autre côté). L’avenir des véhicules électriques représente un bon exemple des difficultés auxquelles peut être confrontée une réflexion prospective (voir FOCUS).
Des méthodes basées sur l’analyse des Big Data (voir Tangente 181, 2018) et faisant appel à l’intelligence artificielle (voir notre hors-série sur le sujet, 2018) sont en plein développement et vont sans doute bouleverser les méthodes de prévision. Elles sont certainement très efficaces pour suivre des tendances à un moment donné. Toutefois, en raison de l’extrême sensibilité aux perturbations des évolutions suivies par les systèmes complexes non linéaires, elles ne devraient pas, pour autant, permettre d’anticiper un avenir à plus long terme. De ce fait, la méthode des scénarios restera sans doute pendant longtemps l’un des principaux outils de la prospective.
Alexandre Rojey est le fondateur du think tank IDées de la Fondation Tuck. Il est l’auteur d’ouvrages sur l’énergie et la prospective, dont le Monde qui vient (Libre et Solidaire, 2018).
Lire la suite