
Les assureurs ont pour mission d’offrir à leurs clients une protection contre les nombreux risques auxquels ils peuvent être confrontés. Compte tenu de la nature financière de cette protection, le secteur est strictement contrôlé, de sorte que la solvabilité des assureurs soit garantie, dans l’intérêt des assurés.
L’assurance consiste à jouer un rôle de mutualisation entre les personnes concernées. Leur collectivité a un comportement souvent largement connu en moyenne (en application de la loi des grands nombres), ce qui permet de mutualiser les risques qui seront avérés pour certains clients et pas pour d’autres. La mutualisation peut être publique (sécurité sociale) ou privée (assureurs). Elle peut être obligatoire (responsabilité civile automobile) ou volontaire (assurance décès complémentaire).
Le rôle de l’assureur privé est de prendre le risque de l’infortune de son client contre le paiement d’une prime. La « prime » est due en amont, en échange d’une couverture dont on ne sait pas a priori si elle aura à être actionnée. C’est le cycle inversé de production, alors que dans le commerce traditionnel, on obtient un produit physique au moment de son achat. Le risque doit être clairement défini et sa réalisation doit être aléatoire. Une garantie d’indemnisation, dans le cas où le risque serait avéré (on parle alors de survenance d’un sinistre), doit être également précisée.
L’assurance se décline sous différentes formes, suivant les cas pour les clientèles de particuliers ou d’entreprises : assurance en cas de vie et en cas de décès (via des prestations d’épargne et de retraite, ou des indemnisations), assurance santé et prévoyance (via des prestations pour des soins ou en cas d’accidents de la vie comme une incapacité, une invalidité ou une période de chômage), assurance de responsabilité (soit familiale, soit d’entreprise), assurance de biens (notamment automobiles, habitations ou locaux professionnels, vol, casse). Depuis les origines de l’assurance, que l’on peut situer à l’époque des Babyloniens près de deux mille ans avant notre ère en lien avec le transport maritime, les outils mathématiques se sont développés.

La tarification, une pratique traditionnelle
La tarification est réalisée en amont de la distribution du produit. L’essentiel de l’estimation consiste à définir la prime de risque en s’appuyant sur les bases techniques disponibles. La tarification suit des modalités largement différentes suivant que l’on traite d’assurances en cas de vie ou décès ou d’autres types de produits.
Pour les assurances en cas de vie ou de décès, les paramètres essentiels pris en compte dans la tarification sont d’une part un taux d’actualisation, permettant de connaître la valeur actuelle des flux anticipés dans le futur, et d’autre part la probabilité de décès ou de survie de la personne assurée (couverture en cas de décès, de vie ou de retraite) ainsi que les garanties accordées (du capital, d’un taux de revalorisation annuel, des caractéristiques d’une rente future…). Les probabilités de décès et de survie aux différents âges de la vie font l’objet de tables de mortalité (ou de mortalité prospective pour les rentiers, qui ont une espérance de vie supérieure à la moyenne de la population) : elles se traduisent généralement en partant d’une population type de cent mille personnes et en dénombrant le nombre de personnes restant en vie année après année. Ces tables sont mises à jour périodiquement pour tenir compte des évolutions de l’espérance de vie.
Pour les autres assurances, en particulier l’assurance automobile ou habitation, la tarification s’appuie sur l’expérience disponible en termes de sinistralité des contrats en portefeuille. L’enjeu est d’expliquer les niveaux de risque constatés (nombre de sinistres et coût moyen des sinistres pour chaque assuré) grâce à plusieurs paramètres. Ainsi, en assurance automobile, on intègre le type, l’âge et la puissance du véhicule, le lieu de résidence, le type de stationnement, le nombre de conducteurs, l’âge du conducteur, l’historique de sinistralité. Les bases techniques doivent donc faire l’objet de régressions statistiques permettant une explication de la sinistralité, et donc une tarification la plus fine possible. Ce qui suppose en amont des retraitements de données, pour éliminer des données non signifiantes ou aberrantes.
Tous ces traitements aboutissent in fine au calcul d’une prime de risque à laquelle il convient, pour arriver à la prime commerciale, d’ajouter les frais de gestion et de distribution ainsi qu’une marge de rentabilité pour l’assureur. Cette dernière est fonction du capital que l’assureur est tenu de mobiliser pour l’activité, appelé exigence de solvabilité.
Provisionnement et solvabilité, des enjeux renouvelés
Le provisionnement est réalisé périodiquement en parallèle du déroulement des contrats et de la gestion des sinistres. Il consiste à calculer dans le bilan de l’assureur le montant des engagements résiduels envers les assurés, de sorte qu’il soit capable de les indemniser intégralement.
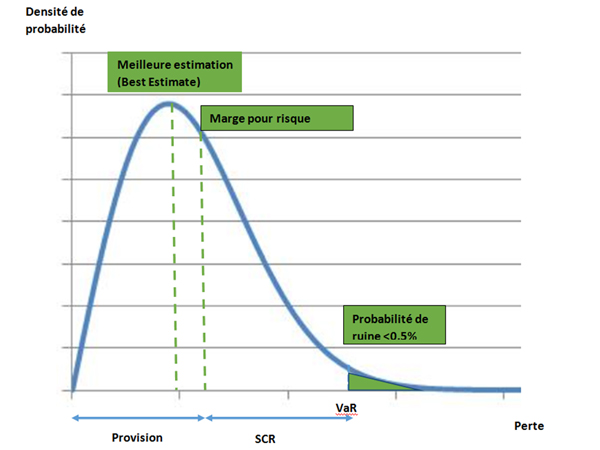
Les calculs de provisionnement ont historiquement largement reposé sur des méthodes déterministes, qui ont laissé place à des méthodes stochastiques permettant d’obtenir une meilleure estimation (bestestimate) grâce à des générateurs de scénarios économiques (voir FOCUS).
En assurance vie, la modélisation doit prendre en compte des interactions actif passif, notamment les comportements des assurés sur le stock de contrats résiduels ainsi que les modalités d’attribution de participation aux bénéfices par l’assureur. Pour les autres assurances, c’est la modélisation du passif (largement indépendante de celle de l’actif modulo le taux d’actualisation) qui tient une place essentielle pour estimer le rythme d’écoulement des engagements résiduels et leur montant terminal : en s’appuyant sur les chroniques de paiement de sinistres déjà connues (appelées triangles de liquidation), on évalue les règlements futurs sur les sinistres en cours.
Une fois le provisionnement calculé (en best estimate), une marge pour risque est ajoutée pour obtenir la provision imputée au bilan.
Le calcul de l’exigence de solvabilité a longtemps été effectué forfaitairement à partir des montants de primes et de provisions. À partir de 2016, est entrée en vigueur en Europe la directive Solvabilité II, qui a introduit une vision plus économique des risques portés par les assureurs. Pour la quantification des risques, l’outil financier retenu est la mesure de la value at risk (VaR), qui correspond au montant de pertes maximal qui ne devrait être dépassé qu’avec une probabilité inférieure à 0,5 % sur l’horizon temporel (un an). Ainsi, le capital de solvabilité requis (SCR), au-delà des provisions, correspond à une probabilité de ruine à un an de l’assureur inférieure à 0,5 %, ou encore d’une faillite au maximum tous les deux cents ans.
En pratique, le SCR est calculé en décomposant le risque en risques élémentaires, en disposant pour chacun d’eux d’un choc élémentaire défini dans la réglementation pour représenter un événement bicentenaire, puis en mesurant sur la base de simulations stochastiques le montant de pertes maximal correspondant au choc pour chaque risque élémentaire identifié. Enfin, on agrège les montants correspondants.
L’exigence de solvabilité mesurée par le calcul doit être couverte par des éléments de fonds propres qui incluent à la fois le capital, des titres de dette et la richesse latente correspondant aux flux futurs projetés dans le calcul de l’exigence, permettant ainsi une vision véritablement économique de la solvabilité.
Les mathématiques au cœur de nouveaux métiers
Les applications mathématiques bénéficient d’une « matière première », les données, qui s’est considérablement enrichie en même temps que les capacités de stockage et de traitement. L’analyse de textes ou de la voix est par exemple aujourd’hui possible. Un enjeu majeur est d’assurer la qualité des données, seule garante de leur bonne utilisation à grande échelle.
On peut schématiquement distinguer deux types de développement de l’utilisation des mathématiques. En premier lieu, la modélisation prédictive consiste à identifier puis répliquer les déterminants de certains phénomènes ; en assurance, cela permet de mieux mesurer les risques, solliciter des clients les informations nécessaires au traitement de leurs demandes et leur apporter des réponses adaptées. Ce type de modélisation s’est développé récemment, par exemple avec la mise en place de pricing dynamique, qui adapte le tarif des produits en quasi temps réel aux évolutions de l’environnement et de la concurrence. Ces modélisations, y compris le risque résiduel de leurs imperfections, font partie intégrante du métier de l’assureur.
En second lieu, la réplication de tâches humaines consiste à automatiser certains traitements au sein de l’entreprise et vis-à-vis des clients. Grâce à des outils d’intelligence artificielle, on peut par exemple automatiser des opérations ayant peu de valeur ajoutée sur des fichiers informatiques, écouter et analyser le déroulement des processus de vente, lutter contre la fraude ou encore, dans les phases de gestion de sinistres, télécharger des documents justificatifs et automatiser leur traitement et la réponse aux clients.
Ces nouvelles possibilités permettent d’améliorer la vitesse du traitement des dossiers et la profondeur d’analyse. Certains contacts humains avec le client s’en trouvent réduits, mais l’assureur ne pourra pas les remplacer tous, que ce soit à des phases clés comme le conseil au moment de la vente ou bien encore à la demande du client. Des métiers sont amenés à disparaître ou à évoluer au profit de métiers émergents à plus forte valeur ajoutée. Aussi, les entreprises d’assurance diversifient leurs personnels et recherchent des profils experts dans l’analyse et le traitement des données, ou à même de faire le lien entre les besoins des métiers de l’entreprise et les outils scientifiques disponibles. Ces profils peuvent être identifiés en interne, quitte à former les personnes à cet effet, ou recrutés en externe. Des directions dédiées à ces métiers peuvent être créées (c’est le cas chez BNP Paribas Cardif).
L’utilisation des mécanismes classiques d’actualisation de flux dans les directions techniques des assureurs a été complétée par l’utilisation de modélisations stochastiques, qui continuent à s’affiner. Les applications mathématiques ont élargi leur « terrain de jeu » dans l’entreprise et se retrouvent maintenant dans toute la chaîne de valeur des assureurs et les parcours clients.
Xavier Cognat est directeur des affaires institutionnelles de BNP Paribas Cardif.
Lire la suite