Deux théorèmes pour le prix d'un

Le mot « dual »s’applique en mathématiques de multiples façons : on parle de dual d’un espace vectoriel (voir article « L'échangisme en géométrie » ), d’un polyèdre, d’un graphe, et même de dual d’un théorème. Cette notion de « théorèmes duaux » est fondamentale. Le domaine de la géométrie projective est tout indiqué pour illustrer l’importance de la dualité.

Si les objets auxquels on applique le mot « dual » sont différents, un même phénomène est en fait à l’œuvre : à partir d’un ensemble E d’objets, si l’on peut associer, par une bijection, à tout élément X de E un élément Y d’un autre ensemble E*, on dit que E* est le dual de E. Ainsi, le dual du dual de E est E lui-même. La signification précise du mot peut toutefois prendre, selon les cas, diverses formes. Un premier exemple, élémentaire, est celui du complémentaire d’un ensemble : à tout élément X de l’ensemble \( {\cal P}(E)\)   des parties d’un ensemble donné E, on associe son complémentaire X’ dans E. L’ensemble   \( {\cal P}(E)\) est son propre dual dans cette opération.

Le dual du tétraèdre est un tétraèdre, le dual d’un octaèdre est un cube (et réciproquement), le dual d’un dodécaèdre est un icosaèdre (et inversement).

Le dual d’un graphe

La notion de graphe dual généralise celle de polyèdre dual (voir article « Quand les polyèdres vont deux par deux » ). Un graphe G est un ensemble de points (les sommets) dont certains sont reliés (par des arêtes).

Le graphe dual G’ de G est le graphe obtenu en remplaçant chaque face (ou cellule) de G par un sommet, et en transformant chaque arête de G (entre les deux points qu’elle relie) en une arête de G’ (entre les deux cellules qu’elle sépare). Ainsi, deux sommets de G’ sont reliés si, et seulement si, les cellules de G qui leur correspondent partagent une arête.

Le dual (G’)’ du dual G’ d’un graphe G est G lui-même.

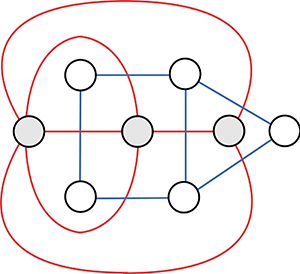
En bleu, le graphe G, constitué de cinq sommets et six arêtes, délimite trois cellules
(dont la « face extérieure » à G).
En rouge, le graphe dual G’ de G est constitué de trois sommets et six arêtes.

La dualité, étendue aux théorèmes, va permettre à peu de frais d’en inventer de nouveaux : en remplaçant des objets par leurs duaux, on peut transposer un théorème qu’ils vérifient et créer ainsi un théorème « dual » du premier, dont la démonstration se fera aisément.

Voyage en géométrie projective

C’est en géométrie projective, née avec le Traité des propriétés projectives des figures de Jean-Victor Poncelet en 1822, que l’on illustre le mieux la notion de théorèmes duaux. Cette géométrie repose sur le fait que par deux points passe une droite et une seule (comme en géométrie euclidienne), et que deux droites distinctes se coupent toujours en un point et un seul (« à l’infini » dans le cas où ces droites sont parallèles). Ces deux propositions sont déjà duales l’une de l’autre, puisque l’on passe de l’une à l’autre en échangeant les mots « droites » et « points » ; c’est cette caractéristique qui va créer des théorèmes duaux.

L’un des résultats les plus connus de géométrie projective est le théorème de Desargues, mathématicien et architecte lyonnais du XVII^e siècle :

Prenons deux triangles ABC et A’B’C’. On note X = [BC], Y = [AC], Z = [AB], X’ = [B’C’], Y’ = [A’C’] et Z’ = [A’B’]. Les points P, Q et R sont définis ainsi : 
\( X\cap X'=\{P\}, \,\, Y\cap Y'=\{Q\}\,\, \hbox{et}\,\, Z\cap Z'=\{R\}.\)  
Enfin, on introduit trois droites : D = (AA’), E = (BB’) et F = (CC’). Alors dire que P, Q et R sont alignés équivaut à dire que D, E et F sont concourantes.

Passer au dual en échangeant « droites » et « points » donne ceci :

Prenons deux triangles de côtés respectifs a, b, c et a’, b’, c’. On note leurs sommets
\( X\!= b\,\cap\, c\, ,\, Y\!=a\,\cap\, c\, ,\, Z\!=b\,\cap\, a\, ,\, X'\!=b'\,\cap\, c'\, ,\, Y'\!=a'\,\cap\, c'\, ,\, \hbox{et}\,\,\, Z'\!=b'\,\cap\, a' .\)

Si P est la droite (XX’), Q la droite (YY’), R la droite (ZZ’) et D le point \( a\cap a',\) E le point \( b\cap b',\) F le point \( c\cap c',\) alors dire que les droites P, Q, R sont concourantes équivaut à dire que les points D, E, F sont alignés.

Un peu décevant, non ? On retrouve le même résultat : le théorème de Desargues est autodual. Mais soyons rassurés : par dualité, on peut aussi fabriquer vraiment de nouveaux théorèmes.

D’autres configurations duales classiques sont celle des théorèmes, bien connus eux aussi, de Ménélaüs et de Céva. Tout commence avec le géomètre d’Alexandrie Ménélaüs qui, au i^er siècle de notre ère, dans le troisième tome de son ouvrage Sphaerica, énonce le résultat qui va porter son nom. Il le formule, comme en son temps, en termes de longueurs ; nous pourrions aujourd’hui l’énoncer sous la forme suivante :

Les trois points P, Q, R situés respectivement sur les côtés [BC], [CA], [AB] d’un triangle ABC sont alignés si, et seulement si,
\( \frac{PB}{PC}\times \frac{QC}{QA}\times \frac{RA}{RB}=1\)

(les points P, Q et R peuvent, en géométrie projective, être alignés sur une parallèle à (BC), le théorème prenant alors la forme de celui de Thalès).

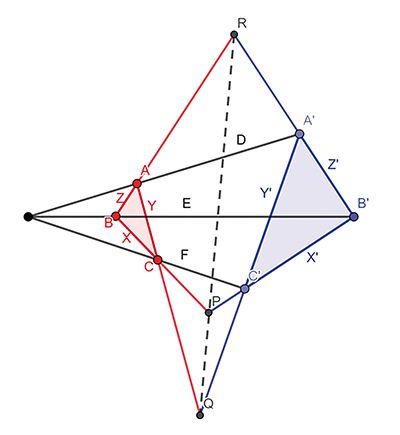
Une configuration du théorème de Desargues.

L’affaire se poursuit environ quinze siècles plus tard avec le mathématicien italien Giovanni Ceva qui, redécouvrant le théorème de son illustre prédécesseur, énonce, toujours avec des longueurs, le théorème à qui on donnera aussi son nom :

Les trois droites contenant les sommets A, B et C d’un triangle et coupant les côtés opposés en P, Q et R respectivement, sont concourantes si, et seulement si,
\( \frac{PB}{PC}\times \frac{QC}{QA}\times \frac{RA}{RB}=1\)
(le terme « concourant » étant au sens de la géométrie projective, c’est-à-dire que les droites sont « concourantes ou parallèles » en géométrie affine).

On reconnaît la forme duale du théorème de Ménélaüs, où on ne parle plus du triangle en termes de côtés, mais de sommets, et où les éléments duaux des points sur les côtés sont les céviennes, ces droites qui passent par les sommets pour couper le côté opposé. La condition d’alignement des points sur les côtés du triangle devient alors celle du concours des céviennes.

On énonce aujourd’hui ces deux résultats en utilisant des mesures algébriques, ce qui conserve le « 1 » du premier théorème (un seul des points P, Q ou R est extérieur au côté qui le porte) et transforme le « 1 » en « –1 » dans le second (les pieds des trois céviennes sont intérieurs aux côtés correspondants).

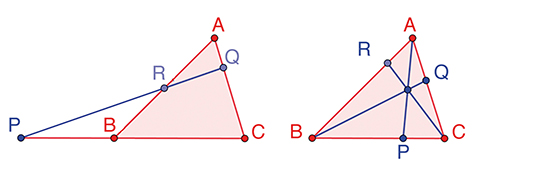
Les théorèmes de Ménélaüs (à gauche) et de Céva (à droite).

L’hexagramme mystique

Un dernier exemple célèbre est celui que Blaise Pascal appelait « l’hexagramme mystique », et dont il a fait un théorème de son Traité des coniques en 1648. Il s’énonce ainsi :

Étant donnés six points A, B, C, A’, B’ et C’ sur une conique, si l’on définit les droites X = (AB’), X’ = (A’B), Y = (AC’), Y’ = (A’C), Z = (BC’) et Z’ = (B’C), alors les points

\( P\!=X\cap X', \,Q\!=Y\cap Y' \hbox{ et } R=Z\cap Z'\)

 sont alignés.

Par passage au dual, on obtient :

Étant donnés six droites A, B, C, A’, B’ et C’ tangentes à une conique (la figure duale K’ d’une conique K du plan reste une conique et un point de K devient la tangente en ce point), si l’on définit les points

\( X\!= \!A\cap B',\, X'\!\!= A'\cap B,\, Y\!\!= A\cap C',\, Y'\!\!= A'\cap C,\, Z\!= \!B\cap C',\,\hbox{et}\, Z'\!= B'\cap C,\,\)
alors les droites P = (XX’), Q = (YY’) et R = (ZZ’) sont concourantes.

Voilà cette fois un nouveau théorème : c’est le résultat que le mathématicien français Charles-Julien Brianchon (1783–1864) publia dans un article Sur les surfaces courbes du second degré, dans le Journal de l’École polytechnique alors qu’il était encore étudiant. Il est évidemment connu sous le nom de théorème de Brianchon et c’est exactement le dual du théorème de Pascal.

Le principe de dualité, qui permet d’obtenir « deux théorèmes pour le prix d’un », montre qu’en fait, ce qui est important, ce sont les relations d’incidence indiquant « tel point appartient à telle droite » ou « telle droite passe par tel point », et non la nature ou le nom de ces droites ou de ces points. On rejoint là ce que disait le mathématicien allemand David Hilbert (1862–1943) : « Les mathématiques sont un jeu que l’on exerce selon des règles simples en manipulant des symboles ou des concepts qui n’ont en soi aucune importance particulière », allant même jusqu’à dire qu’il « doit toujours être possible de substituer “table”, “chaise” et “chope de bière” à “point”, “droite”, “plan” dans un système d’axiomes géométriques ».

L’hexagramme mystique (à gauche) et le théorème de Brianchon (à droite).