La formule d’Euler affirme que, pour un polyèdre, sous certaines conditions, si S désigne le nombre de sommets, F le nombre de faces et A le nombre d’arêtes, on a la relation

S + F – A = 2.

Elle est extraordinaire à plus d’un titre (voir le dossier consacré à cette formule dans Tangente 174, 2017). Extraordinaire de simplicité, elle lance un pont entre la géométrie (les polyèdres) et l’arithmétique (S, F et A sont des nombres entiers). Elle introduit en outre la notion de dualité…

On lit souvent que le tétraèdre est « son propre dual ». En fait, le dual du tétraèdre est un autre tétraèdre. Dans l’opération de dualité, on fait correspondre à un sommet une face. Plus précisément, à un sommet où convergent n faces et n arêtes, on peut faire correspondre une face possédant n côtés, et réciproquement (à une face à m côtés on peut faire correspondre un sommet où convergent m faces et arêtes).

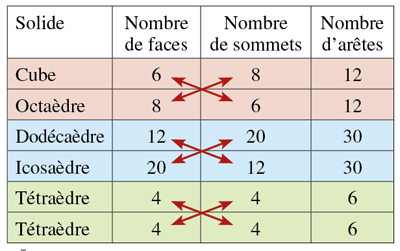
Les solides de Platon et leurs polyèdres duaux.

Pour les solides de Platon, la recette pour obtenir le polyèdre dual est assez simple : il suffit de prendre les centres des faces. Le polyèdre dual est alors l’enveloppe convexe des centres des faces, c’est-à-dire le « plus petit » polyèdre contenant ces points. Pensez à une enveloppe à l’intérieur de laquelle on ferait le vide : cette enveloppe viendrait « se plaquer » sur les points « les plus à l’extérieur ».

Pour simple à exprimer qu’elle soit, cette méthode est assez difficile à mettre en œuvre : elle suppose de maîtriser la technique de l’enveloppe convexe. Voyons-en donc une deuxième méthode. La détermination des sommets est toujours aussi simple, il s’agit des centres des faces. Les nouvelles faces vont être orthogonales aux droites reliant les sommets du polyèdre de départ au centre. Donc il suffit de faire glisser ces plans en partant d’un sommet du polyèdre de départ vers le centre du polyèdre d’arrivée, jusqu’à ce que l’on rencontre des nouveaux sommets ; on obtient alors une face, qui est un polygone convexe.

Si l’on est en présence d’un solide platonicien et de son dual, on peut choisir leur taille de façon à ce que leurs arêtes respectives se croisent orthogonalement en leurs milieux. Chaque paire d’arêtes orthogonales forme les diagonales d’un losange. L’ensemble de ces losanges, qui sont aussi l’enveloppe convexe (voir FOCUS) des deux polyèdres, forme un polyèdre rhombique. Le noyau de ces deux polyèdres duaux, c’est-à-dire le « plus grand » polyèdre contenu à l’intérieur de deux polyèdres, est quasi-régulier et dual du polyèdre rhombique !

De cette manière, on découvre deux solides archimédiens, le cuboctaèdre et l’icosidodécaèdre, et leurs duaux respectifs, le dodécaèdre rhombique et le triacontaèdre rhombique.

De son côté, le système tétraédrique nous indique simplement que le cube et l’octaèdre sont duaux, ce que l’on savait déjà. Que dire pour les autres solides, comme par exemple les treize polyèdres archimédiens (qui ne sont pas réguliers mais semi réguliers) ? Pour eux, la procédure est moins immédiate. Car si l’on prend l’enveloppe convexe des centres des faces, on n’obtient pas le polyèdre désiré. Il faudra en fait attendre Eugène Charles Catalan (1814–1894) pour résoudre le problème (Mémoire sur la théorie des polyèdres, 1865). Les polyèdres archimédiens possèdent des sommets qui se présentent sous la même forme, leurs duaux n’auront donc qu’un seul type de face !

Des sphères pour un polyèdre

On peut associer trois sphères à chaque solide de Platon : la sphère circonscrite (passant par tous les sommets), la sphère milieu (passant par tous les centres des arêtes) et la sphère inscrite (passant par tous les milieux des faces). Cependant, on ne peut en associer qu’une aux polyèdres archimédiens : la sphère circonscrite. Catalan va procéder par conjugaison par rapport à cette sphère pour obtenir les duaux des archimédiens, duaux qui prendront le nom de polyèdres de Catalan, même si le dodécaèdre rhombique et le triacontaèdre rhombique étaient déjà connus de Johannes Kepler.

Pour chaque face, on détermine sa normale passant par le centre O du polyèdre. Cette normale coupe cette face en M. Le nouveau sommet M’ se trouve sur cette normale et vérifie \( \overline{OM}\times \overline{OM'}=R^2,\) R étant le rayon de la sphère de conjugaison.

Pour chaque sommet M, le point M’ sur la droite (OM) vérifie \( \overline{OM}\times \overline{OM'}=R^2.\) Soit P le plan de normale (OM) et passant par M’. P est le plan d’une face du polyèdre dual ; il suffit de regarder quels sommets, précédemment déterminés, appartiennent à P, ces sommets déterminent une face du polyèdre dual. Pour les solides de Catalan, ces faces sont convexes.

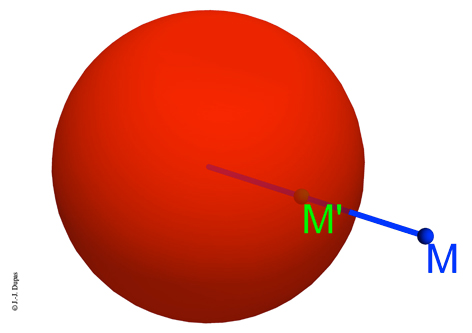
Conjugaison par rapport à la sphère rouge.
Le point M’ est le conjugué du point M, et réciproquement.

Les étoiles de Kepler (à savoir, le petit dodécaèdre étoilé et le grand dodécaèdre étoilé) possèdent également des polyèdres duaux. Malheureusement, Kepler ne les rechercha pas. Il faudra attendre 1809 et Louis Poinsot pour mettre en évidence ces objets. Le dual du petit dodécaèdre étoilé {5/2, 5} est le grand dodécaèdre {5, 5/2}, et le dual du grand dodécaèdre étoilé {5/2, 3} est le grand dodécaèdre {3, 5/2}.

Le petit dodécaèdre étoilé {5/2, 5} (à gauche) 
et le grand dodécaèdre étoilé {5/2, 3} (à droite).

Les polyèdres de Poinsot–Kepler sont des polyèdres réguliers non convexes. Comme pour les solides de Platon, si l’on considère une étoile et son dual, de telle sorte que leurs arêtes se croisent orthogonalement en leurs milieux, alors on obtient, en gardant toutes les figures de sommets de ces deux polyèdres, deux polyèdres uniformes quasi réguliers. La figure de sommet du sommet S d’un polyèdre est un polygone. Ce polygone est la base d’une pyramide de sommet S, obtenue en coupant S à une distance constante sur chaque arête (choisir la demi-longueur de l’arête permet souvent de simplifier les constructions).

L’idée est de remplacer le sommet S (point unique) en un polygone qui sera plus éclairant sur la nature de S. La figure de sommet permet par exemple de caractériser plus simplement les polyèdres réguliers : un polyèdre est régulier si toutes ses figures de sommet sont d’un même type de polygone régulier. Le cube est donc un polyèdre régulier puisque toutes ses figures de sommet sont des triangles équilatéraux.

La figure de sommet du coin qui « pointe vers nous » est le triangle équilatéral bleu.

Chacun des polyèdres de Poinsot–Kepler possède un polyèdre dual rhombique dont les diagonales sont les arêtes des polyèdres de départ (toujours comme dans le cas des solides de Platon, seulement ici on ne peut pas utiliser la convexité). Ces deux polyèdres rhombiques sont des triacontaèdres rhombiques. Une version simplifiée de cet objet sert de logotype pour les anciennes versions du logiciel Mathematica ^(R) (Wolfram Research, 1988).

Les duaux des polyèdres uniformes, avec leur nomenclature.

(télécharger la page en pdf)

Bon pour l’uniforme

Les polyèdres uniformes, enfin, sont ceux dont les faces sont des polygones réguliers, étoiles comprises ; il faut par ailleurs qu’il existe un groupe de symétrie qui transforme un sommet en tous les autres. Les solides de Platon, les étoiles de Poinsot–Kepler, les polyèdres archimédiens, les prismes, les anti-prismes sont des cas particuliers des polyèdres uniformes.

Regardons quelques polyèdres uniformes non convexes. Pour eux, la méthode de Dorman Luke* fonctionne à tous les coups, mais la figure de sommets ne va pas toujours avoir une forme élémentaire (ce peut être un polygone croisé par exemple). Difficulté supplémentaire : les faces du dual peuvent se croiser, donc la méthode ne fournira pas la forme externe de la face mais son enveloppe. Il arrive couramment que certains sommets du dual se trouvent cachés « à l’intérieur » du polyèdre !

Magnus Wenninger (1919–2017, voir les Surfaces, hors-série 71 de Tangente, 2019) conjectura que le dual d’un polyèdre uniforme est une étoile du dual de l’enveloppe convexe du polyèdre uniforme de départ. Cette hypothèse, qu’il vérifia lui-même par disjonction des cas, relie la dualité et le processus d’étoilement. Comme plusieurs polyèdres uniformes non convexes possèdent la même enveloppe convexe, il se trouve que plusieurs polyèdres uniformes non convexes possèdent le même dual… Enfin, certains polyèdres uniformes possèdent des faces dont le plan passe par le centre du polyèdre, ce qui « rejette à l’infini » les faces du dual. 

Fascinants objets géométriques que les polyèdres !

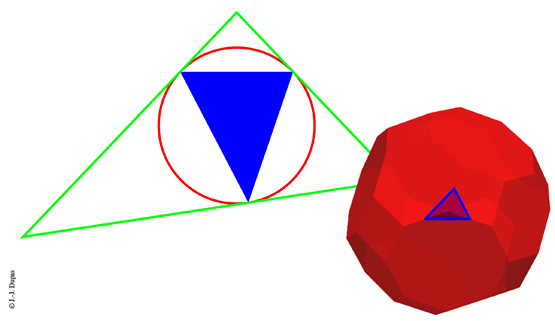
À gauche : la figure de sommet du grand rhombicuboctaèdre (en bleu), 

le cercle circonscrit (en rouge), la forme de la face du polyèdre dual (en vert). 

À droite : une des figures de sommet du grand rhombicuboctaèdre.

* Prendre la figure de sommets du polyèdre dont on veut connaitre le dual, en déterminer le cercle circonscrit. Les côtés de la face du dual sont les tangentes, sur ce cercle circonscrit, aux sommets de la figure de sommets (cf. schéma ci-dessus).