
On ne parlait pas de dualité en mathématiques avant le début du XIXe siècle. On s’y réfère alors avec le développement de la géométrie projective, promue par Gaspard Monge, Lazare Carnot, Victor Poncelet et Joseph Diez Gergonne (voir notre dossier dans Tangente 162, 2014). Ce dernier s’est émerveillé que « dans cette partie de la géométrie, qui ne dépend aucunement des relations métriques entre les figures, […] à chaque théorème, il en répond nécessairement un autre qui s’en déduit en échangeant simplement entre eux les deux mots “point” et “droite” ». Dans l’espace, explique-t-il, les mots « point » et « plan » jouent le même rôle ; il parle alors de « cette sorte de dualité des théorèmes qui constituent la géométrie de situation ». Le mot était lâché !

à gauche : Gaspard Monge (1746–1818), comte de Peluse, en habit de président du Sénat.
à droite : Lazare Nicolas Marguerite Carnot (1753–1823), L’Organisateur de la Victoire.
Le sens de « dualité » s’est élargi plus tard pour désigner, de manière générale, toute situation où deux éléments, deux espaces, deux figures jouent des rôles symétriques l’un par rapport à l’autre. Un bel exemple de théorèmes duaux nous est donné avec ceux de Pascal et de Brianchon. Quant à celui de Desargues, il est autodual, c’est-à-dire que l’on retrouve le même théorème après inversion des mots « point » et « droite » (voir article « Deux théorèmes pour le prix d'un »).
Intervertir « point » et « droite »
À qui doit-t-on la mise en lumière du principe de dualité dans les théorèmes de géométrie projective, c’est-à-dire celle qui concentre son intérêt sur les propriétés invariantes par projection centrale ? Les précurseurs sont certainement Monge et Carnot, le premier en développant la géométrie descriptive et le second en remplaçant les longueurs par les mesures algébriques.

Jean-Victor Poncelet (1788–1867), Grand Officier de la Légion d’honneur.
Poncelet, le miraculé de la bataille de Krasnoï en 1812, où il est fait prisonnier, reconstitue dans sa prison de Saratov ses connaissances en géométrie, en particulier les cours des deux mathématiciens précédents. Allant plus loin, il jette les bases de cette nouvelle géométrie. C’est lui sans doute qui, le premier, a compris la dualité que l’on obtient en intervertissant le rôle des points et des droites ; son Mémoire sur la théorie générale des polaires réciproques (1819) et son Traité des propriétés projectives des coniques (1822) en témoignent.

Joseph Diez Gergonne (1771–1859),
membre de l’Académie royale des sciences de Prusse.
C’est alors qu’apparaît un quatrième larron. Élève de Monge, Gergonne, un mathématicien d’origine lorraine installé en Languedoc, fait paraître, de 1810 à 1831, les Annales de mathématiques pures et appliquées, revue où furent publiés de nombreux articles de recherches à visée didactique. Gergonne y développe de nombreux résultats de géométrie projective, en mettant chaque fois en lumière le théorème dual. Il laisse aussi à d’autres, en particulier Poncelet, la possibilité de s’exprimer dans ses colonnes. Persuadé d’avoir révolutionné la géométrie, Gergonne s’oppose alors vivement à Poncelet sur la prééminence de la découverte de la dualité (voir FOCUS).
Pôles et polaires
L’échange entre les termes « point » et « droite » est clairement visible dans les notions de pôles et polaires, mots que l’on doit au mathématicien François-Joseph Servois (1768–1847). Considérons une ellipse, ou même un cercle, notée C. D’un point M extérieur à cette courbe, on peut tracer deux tangentes en des points A et B de celle-ci. La droite D qui joint A et B s’appelle la polaire de M. Inversement, pour toute droite D intersectant la courbe en deux points A et B, traçons les tangentes aux deux points A et B ; le point M d’intersection de ces deux droites est le pôle de D.
La propriété clé est que le pôle de la polaire de M est M lui-même et que la polaire du pôle de D n’est autre que D. Pour un point M placé sur C, la polaire est la tangente en M à C, et inversement, le pôle d’une tangente est le point de tangence.
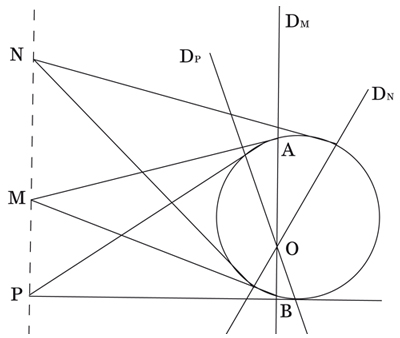
Les polaires respectives des points M, N et P, les droites (DM), (DN) et (DP),
sont concourantes en un point O.
Les notions de pôle et de polaire s’étendent à toute conique, et même, en se plaçant en géométrie complexe, à toute droite puisque l’intersection d’une droite avec la conique contient alors toujours deux points (ou un seul si le point est situé sur la conique).
On obtient des résultats par dualité. Ainsi, si un point M a pour polaire une droite D, alors la polaire de tout point de D passe par M, et inversement le pôle de toute droite qui passe par M se trouve sur D. De même, un point M est sur une droite D si, et seulement si, la polaire de M contient le pôle de D.
De manière générale, d’un théorème, on en obtient un autre en intervertissant les pôles et les polaires : c’est ce que l’on nomme la transformation par polaires réciproques. Ce phénomène renverse les incidences : trois pôles alignés correspondent à trois polaires concourantes, et réciproquement ; quatre points alignés en division harmonique correspondent à un faisceau harmonique de quatre droites (voir notre dossier « Le birapport » dans Tangente 188, 2019).
La dualité dans les espaces vectoriels
Les espaces vectoriels sont devenus de nos jours le cadre de prédilection de l’étude de la géométrie projective (voir Vecteurs et Espaces vectoriels, Bibliothèque Tangente 65, 2018). Aussi la notion de dualité s’est-elle également développée en algèbre linéaire, permettant que, d’une certaine manière, les coordonnées du pôle et l’équation de la polaire se correspondent par dualité.
Les physiciens attribuent souvent un scalaire, c’est-à-dire un nombre, à tout vecteur ou, par analogie, à tout point de l’espace (par exemple la température, l’altitude…). Ainsi s’est développée la notion de forme linéaire, application (ou fonction) f qui attribue à tout vecteur de l’espace E considéré un nombre réel de telle sorte que les égalités
f (u+v) = f (u) + f (v) et f (λu) = λ f (u) soient vérifiées pour tous vecteurs u et v et tout scalaire λ.
L’ensemble de ces formes linéaires constitue un nouvel espace vectoriel E* (« E étoile »), que l’on nomme le dual de E ; il jouit de propriétés analogues à l’espace lui-même : on peut additionner les formes linéaires, les multiplier par un scalaire (voir FOCUS)…
L’analyse s’est ensuite emparée de cette notion. Les formes linéaires « intéressantes » y sont en effet nombreuses ; par exemple celle qui fait correspondre à une fonction son intégrale entre deux bornes. Le dual de l’ensemble des fonctions intégrables joue ainsi un rôle important dans ce domaine.
Et dans la théorie des ensembles !
La théorie des ensembles offre un autre bel exemple de dualité. Prenons un ensemble E et considérons les opérations classiques d’intersection sur les parties de E (l’intersection
et
La seconde formule se déduit logiquement de la première en intervertissant les symboles
Cette dualité se prolonge en fait à bien d’autres formules, à condition d’intervertir E et l’ensemble vide
De cette manière, la dualité se transpose à la logique mathématique, dont les bases avaient été posées par le mathématicien britannique George Boole (1815–1864). En effet, les connecteurs logiques que sont la conjonction (c’est-à-dire « et ») de deux propositions ou leur disjonction non exclusive (c’est-à-dire « ou ») correspondent, respectivement, à l’intersection et à la réunion dans la théorie des ensembles. Ainsi l’interversion de ces deux connecteurs logiques et le remplacement d’une proposition par sa négation donnent des énoncés duaux !
Ces deux théories ont été modélisées dans le cadre des algèbres de Boole. Savoir reconnaître un phénomène de dualité dans un contexte mathématique donné permet bien souvent de s’éviter bien des efforts…
Lire la suite