Le 8 août 1900, c’est l’effervescence à Paris. David Hilbert, mathématicien allemand de 38 ans de réputation internationale, doit prononcer, pour ce siècle qui s’ouvre, un discours lors du second Congrès international des mathématiciens. Après le premier congrès (Zürich, 1897), avec un discours du Français Henri Poincaré, il faut une intervention à la mesure de l’évènement. Ce sera pour le jeune et brillant professeur de l’université de Göttingen l’occasion, selon ses propres termes, de « lever le voile derrière lequel le futur reste caché » et de définir « quelles nouvelles méthodes et quels faits nouveaux le siècle naissant va permettre de découvrir dans le champ fécond de la pensée mathématique ». Ainsi est née l’idée de proposer au monde des mathématiciens une liste de problèmes qui guideraient leurs recherches à venir.

L’avenir des mathématiques

Ci-contre : David Hilbert (1862–1943).

Prononçant son discours lors de la partie commune à deux commissions du Congrès, « Histoire et bibliographie des mathématiques » et « Méthodologie et enseignement des mathématiques », Hilbert insiste sur le rôle éminent de la résolution de problèmes dans l’évolution des mathématiques. 

Il va jusqu’à souligner que « le manque de problèmes signifie la mort ou l’arrêt d’un développement autonome », ajoutant : « Être convaincu qu’un problème mathématique est faisable est un stimulant puissant de notre travail ; nous entendons cette injonction : “Voilà un problème, trouve la solution. Tu peux la trouver par ta seule pensée, car en mathématiques, il n’existe aucun Ignorabimus.” » Poursuivant cette idée que tout problème déterminé peut être résolu, il déclarera même à la radio en 1930 : « Nous devons savoir, nous saurons », inscription qui figure en allemand sur sa pierre tombale. Par le choix de ses vingt-trois défis, Hilbert souhaitait montrer l’unité des mathématiques, et afficher sa confiance dans les résultats des mathématiques à venir. Leur histoire est riche en rebondissements et leur recherche a réellement fait progresser les mathématiques et leur rapport aux autres sciences, en particulier la physique.

Les problèmes de Hilbert liés à la physique sont le sixième (relatif au traitement mathématique des axiomes de la physique), et les numéros 19, 20 et 23 (portant sur le calcul des variations). C’est cependant bien le problème 6 qui rapproche le plus physique et mathématiques. Le souhait de Hilbert à son sujet est de « traiter de la même manière, au moyen d’axiomes, la partie des sciences physiques dans laquelle aujourd’hui déjà les mathématiques jouent un grand rôle, en première ligne le calcul des probabilités et la mécanique ». Les évolutions récentes de la physique moderne, relativité, physique quantique, ont eu raison de son souhait, rendu rapidement obsolète.

Hilbert dédia, à la naissance de la mécanique quantique (bien après 1900), un séminaire à la description de sa structure mathématique. L’un de ses assistants, John von Neumann, Américain d’origine hongroise, poursuivra l’idée de Hilbert de « formuler les exigences de la physique si clairement que le modèle mathématique pourrait n’être dicté que par elles ». C’est lui qui formalisera la théorie quantique en 1932 dans ses Fondements mathématiques de la mécanique quantique. Quant à la formalisation du modèle probabiliste classique, dont parlait Hilbert, elle a été réalisée par Andreï Kolmogorov en 1933 (voir le dossier « Théorie élémentaire des probabilités » dans Tangente SUP 73–74, 2014).

À la recherche de nouveaux concepts 

La stèle de Hilbert.

Les ambitions de Hilbert sur la physique ont fait leur chemin. Elles ont contribué à faire naître de nouveaux concepts mathématiques, comme les espaces de Hilbert (voir FOCUS), que von Neumann a largement exploités, regardant un système quantique comme un vecteur de l’un de ces espaces. Les avancées mathématiques suggérées dans la liste de Hilbert ont par ailleurs été largement utilisées en physique : c’est le cas des trois problèmes 19, 20 et 23 concernant le calcul des variations.

Le premier d’entre eux (« Les solutions d’un problème relevant du calcul des variations sont-elles nécessairement analytiques ? ») prendra son sens dans certaines applications industrielles des mathématiques comme le contrôle optimal (voir le dossier « Prévision des actions humaines » dans Tangente SUP 63–64, 2012).

Le suivant (« Étudier la solution générale des problèmes de valeurs limites ») est une généralisation du problème de Dirichlet (voir FOCUS). Il a été largement repris dans les travaux de Fabrice Bethuel (né en 1963), Haïm Brezis (né en 1944) et Frédéric Helein (né en 1963) sur les cristaux liquides et la supraconductivité, ainsi que dans ceux de Karen Uhlenbeck (née en 1942) sur des équations issues de la physique théorique, les équations de jauge, dont les solutions sont invariantes dans un changement de référentiel. La mathématicienne, qui vient de recevoir le prix Abel 2019 (voir Tangente 188), a su utiliser un cas particulier souvent mis à contribution en théorie de la relativité, la jauge de Coulomb, et en tirer parti en mathématiques pour « faire le tri » dans les solutions parasites.

Le dernier (« Extension du calcul des variations ») a connu lui encore un développement important, en particulier dans l’étude du problème des trois corps.

L’interconnexion physique-mathématiques, après Hilbert, est devenue flagrante : non seulement des problèmes mathématiques permettent de traiter des questions de physique (propriétés de certains alliages, des matériaux magnétiques, segmentation et recoloration d’images…) où les questions de régularité et de convergence interviennent, mais certains problèmes de physique permettent de résoudre des questions ouvertes de mathématiques. Haïm Brezis dit avoir, avec ses collègues Fabrice Bethuel et Jean-Michel Coron, « grâce [aux] réflexions sur les cristaux liquides, pu résoudre un problème ouvert de géométrie en théorie des applications harmoniques » parce que, poursuit-il, ils « avaient en tête de nouveaux outils mathématiques forgés en pensant à ces considérations d’allumettes ».

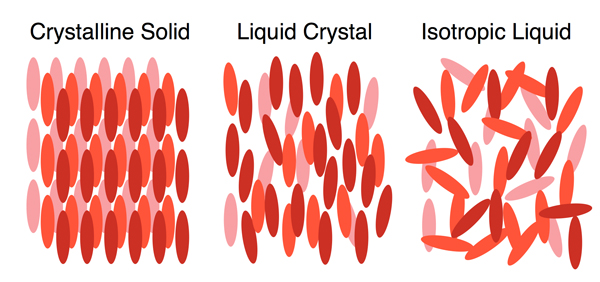
Les cristaux liquides (schématisés au centre) sont des solides dans un état intermédiaire entre les cristaux (à gauche, dont la structure est extrêmement ordonnée et rigide) et les liquides (à droite). Ils peuvent « s’écouler » comme ces derniers mais conservent une structure plus ordonnée.

Que reste-t-il aujourd’hui des problèmes de Hilbert ? Si l’on continue à travailler sur ceux qui ne sont pas résolus et s’il en reste encore beaucoup à approfondir, une nouvelle liste est apparue, celle des « sept problèmes du millénaire », publiée en 2000 par le Clay Mathematics Institute. Cette fois, ils vaudront chacun un million de dollars à ceux qui les résoudront, ce qui n’était pas le cas avec le programme de Hilbert ! Les temps ont changé, mais il demeure, aujourd’hui plus que jamais, une proximité « de cœur » entre les mathématiques et la physique. La « méthode » de Hilbert, que l’on pourrait résumer en « unifier, généraliser, simplifier », est toujours bien présente dans ce rapprochement.