Au début du XIX ^e siècle, Jean-Victor Poncelet étudie les polygones inscrits dans une conique, et circonscrits à une autre. En parcourant le périmètre de tels polygones, on effectue une trajectoire fermée dans une courbe fermée, ce qui est un cas particulier des systèmes dynamiques étudiés par les plus grands mathématiciens, d’Henri Poincaré (1854–1912) à Artur Ávila (né en 1979) en passant par Jean-Christophe Yoccoz (1957–2016). Imaginons qu’une boule de billard se déplace sans frottement et obéisse à la loi de réflexion de Descartes lors d’un rebond sur la bande d’un contour fermé. On parle de réflexion spéculaire (semblable à celle de la lumière sur miroir). La question se pose de savoir s’il existe des trajectoires fermées (dont l’origine et l’arrivée coïncident) pour une forme donnée du billard. Mais ce modèle de billard mathématique, donc parfait, a aussi des applications arithmétiques plus ludiques, comme la résolution de problèmes aqueux, pas si sots (voir FOCUS).

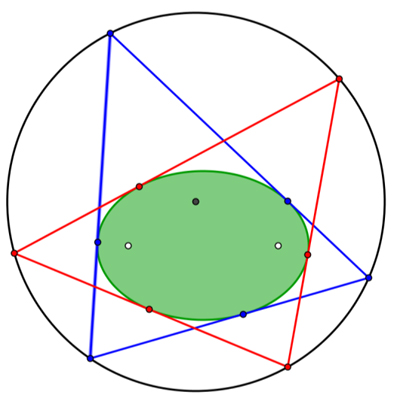
La configuration étudiée par Poncelet. 

Des billards de trajectoires

Autre application intéressante, et inattendue, des trajectoires sur un billard : l’arithmétique. On considère un billard rectangulaire de largeur p sur un axe horizontal et de longueur q sur un axe vertical, dans une unité arbitraire, sur lequel on lance une bille modélisée par un point. Lancée depuis l’un des coins, qui sera pour nous l’origine, selon un angle de 45 degrés, notre bête bille suit les lois de l’optique : son angle de réflexion est égal à son angle d’incidence. Dans les coins, on supposera la bille revenir en sens inverse, et donc parcourir la même trajectoire du fait de la symétrie de la réflexion. Alors notre mobile idéal effectuera une trajectoire périodique entre deux coins. Mais ce n’est pas tout !

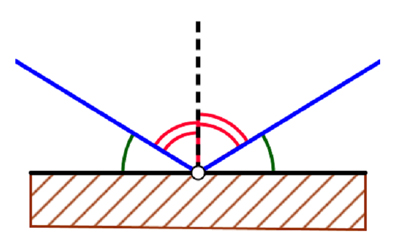
La loi de la réflexion.

Puisque la bille part le long de la diagonale d’un carré unité, il en sera de même tout au long de son parcours d’après les règles de réflexion élastique. Par symétrie, son parcours mesuré sur un côté du billard sera égal à celui mesuré sur le côté perpendiculaire. Pour n carrés traversés, le déplacement, en valeur absolue, sera de n unités sur chacun des côtés du billard. Tous les p carreaux traversés, la bille subit donc une réflexion sur un côté vertical, et tous les q carreaux, une réflexion sur un côté horizontal. Au bout de m carreaux traversés, avec m = PPCM( p, q), le plus petit commun multiple de p et q, la bille atteint à la fois un côté vertical et un côté horizontal, donc un coin.

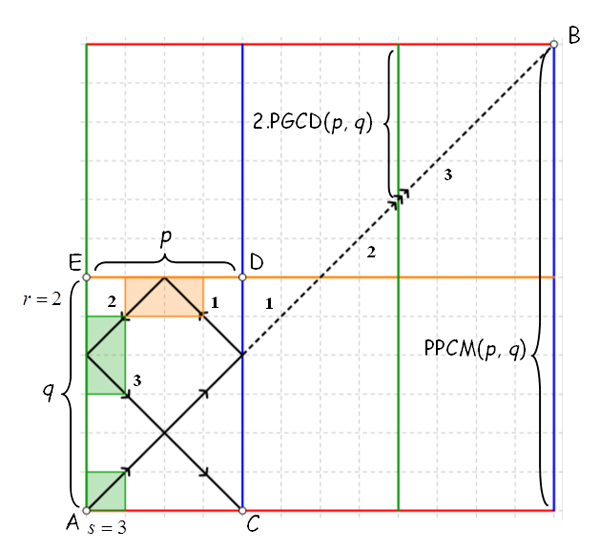
Diviseurs de deux entiers p et q .

Pour visualiser cette trajectoire, au lieu de faire effectuer une réflexion à la bille, on peut la laisser continuer en ligne droite et réaliser une symétrie du billard par rapport au côté touché. On arrive alors au point B en ayant « déplié » la trajectoire sur le billard. En notant d = PGCD( p, q) le plus grand commun diviseur de p et q, il existe des entiers r et s premiers entre eux tels que p = r d et q = s d. Par définition, m = r s d = r q = s p et donc m d = p q : le produit de deux nombres est égal au produit de leur PGCD par leur PPCM. La bille traverse donc toutes les cases pour des nombres premiers entre eux, puisqu’alors m = p q.

Dans ce cas, comme les trajectoires se coupent orthogonalement, la distance de l’origine au rebond le plus proche est de deux unités. En constatant que l’on passe de la trajectoire de (r, s) à celle du couple ( p, q) en divisant simplement l’unité par le PGCD d, on conclut que la distance de l’origine au plus proche rebond est de deux fois d dans le cas général. De plus, r cases sont traversées sur chaque ligne, et s sur chaque colonne. On retrouve le fait que m = r q = s p.

Dans notre exemple, p = 4, q = 6, d’où d = 2, r = 2 et s = 3. C’est pourquoi on compte, sur le trajet développé, s = 3 billards sur l’axe horizontal, à savoir le billard initial et deux images par symétrie (correspondant à s – 1 réflexions), et de même r = 2 billards verticalement (correspondant à s – 1 réflexions).

Le premier coin rencontré par la bille ne peut être son « coin de départ ». Sinon, puisque le déplacement ne s’effectue que suivant les diagonales, le départ et l’arrivée de la trajectoire sont confondus. Alors, en faisant le chemin inverse, on arrive à un embranchement avec deux chemins possibles, ce qui est incompatible avec le déterminisme de la trajectoire. Les seuls points de chute possibles sont donc les coins C, D et E, selon la parité du nombre de rebonds sur les bords verticaux et horizontaux. D’après ce qui précède, si r et s sont impairs, la trajectoire passe par le coin D ; elle passe par C si r est pair et par E si s est pair, sachant que le cas r et s pairs est exclu car correspondant au point de départ A.

Trajets encore billards

Existe-t-il des trajectoires fermées pout tout billard polygonal ? Évitons le cas trivial de trajectoires perpendiculaires à des côtés parallèles, ou le rebond aux sommets du polygone. Une technique utile pour déterminer de telles trajectoires dans le cas général est le « déploiement » du chemin suivi par la boule, comme dans le cas d’un carré, avec un rebond toujours spéc(tac)ulaire. Ainsi, en repliant les segments [OA] et [OB] de la figure suivante, on obtient deux trajectoires périodiques, de quatre et six segments, autant de segments que de carrés traversés.

Déploiement de trajectoires périodiques.

En 1986, Howard Alan Masur a prouvé que dans les polygones rationnels, qui ont pour angles des fractions rationnelles de π, il existe une infinité de trajectoires périodiques. Il est pratique de les obtenir par déploiement, comme indiqué pour le triangle équilatéral.

Trajectoires périodiques dans un pentagone et dans un hexagone.

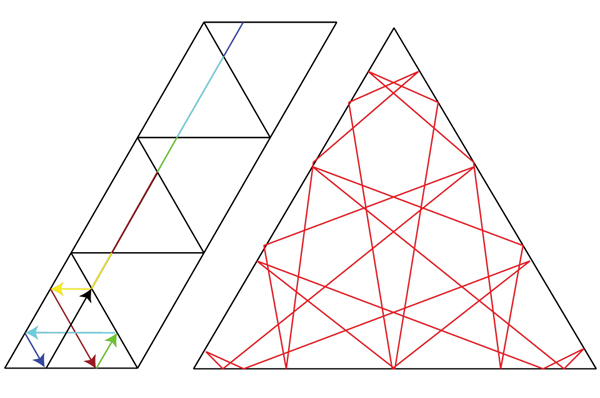
Trajectoires périodiques dans un triangle équilatéral. 
À droite, une trajectoire périodique à vingt-deux rebonds.

Un problème pointu

Pour les triangles aigus, d’angles tous inférieurs à 90 degrés, une solution est donnée par le triangle orthique, ou de Fagnano, du nom du géomètre italien Giovanni Francesco Fagnano dei Toschi (1715–1797). Cherchons un billard admettant un triangle pour chemin périodique. Par définition du rebond, la bissectrice d’un angle doit être normale au côté du billard. En construisant aux sommets du triangle abc les perpendiculaires aux bissectrices, on obtient comme solution un billard triangulaire ABC dont l’orthocentre est le centre du cercle inscrit de son triangle orthique abc. En fait, tout billard perpendiculaire aux bissectrices de abc répond à la question, comme l’hexagone PQRSTU par exemple.

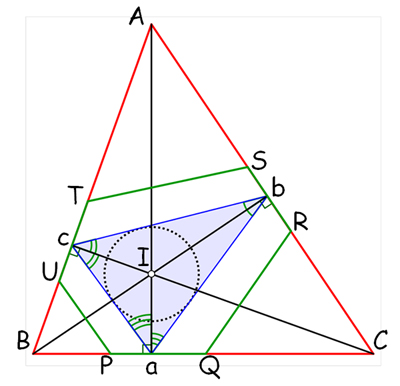
Triangle orthique.

Mais on n’a pu prouver qu’une telle trajectoire périodique existe pour tous les triangles obtus ! Malgré la conviction des spécialistes, ce problème reste aigu. Le mathématicien américain Richard Evan Schwartz a étudié le cas de triangles obtus « proches » du triangle (2, 3, 6) d’une équerre, c’est-à-dire d’angles π /2, π /3 et π /6. Il a donné en 2009 une preuve assistée par ordinateur qu’un triangle admet un chemin périodique si ses angles sont au plus de 100°. Mais impossible de conclure au-delà. Anatole Borisovich Katok (1944–2018) avait même offert une récompense de 10 000 € pour la résolution de ce problème…

Les mathématiques du billard constituent ainsi un chapitre important de la théorie des systèmes dynamiques où de nombreuses questions de formulations simples restent ouvertes.