La cyclide de Dupin
En 1822, dans son livre Application de géométrie, le mathématicien, ingénieur et homme politique français Charles Pierre Dupin présente une surface non sphérique dont toutes les lignes de courbure sont pourtant des cercles. Il les baptise cyclides.
Pour Dupin, une cyclide est l’enveloppe de sphères tangentes à trois sphères fixes. Pour le Britannique Arthur Cayley en revanche, une cyclide est l’enveloppe de sphères dont le centre est dans un plan donné et tangente à deux sphères données. Pour James Clerk Maxwell, par ailleurs, une cyclide est une surface dont toutes les normales passent par deux coniques. La cyclide est enfin l’inversion d’un tore, ce qui explique qu’en tout point y passent quatre cercles : les méridiens (en vert), les parallèles (en bleu) et les images des cercles de Villarceau (en rouge et orange). Le tore est un cas particulier de la cyclide. Les cyclides possèdent un nombre inouï de propriétés, qui font qu’elles servent en infographie pour raccorder des surfaces.
Les carreaux de Bézier
Les carreaux de Bézier, du nom de l’ingénieur français Pierre Bézier (1910–1999), ont été mis au point en 1962 pour modéliser des carrosseries automobiles. Ces carreaux s’appuient sur les courbes de Bézier (voir Tangente 125, 2008), qui s’expriment à l’aide des polynômes de Bernstein. Les carreaux de Bézier se construisent sur une grille de points que l’on déforme. Le paraboloïde hyperbolique en est un cas particulier. Les carreaux de Bézier sont abondamment utilisés dans les logiciels de CAO (conception assistée par ordinateur) et DAO (dessin assisté par ordinateur), car ils sont un moyen efficace de construire des surfaces.
.jpg "J.-J. Dupas, 2019\) </MathML></p>
<p> </p>
<h1> </h1>
<h1 style=")
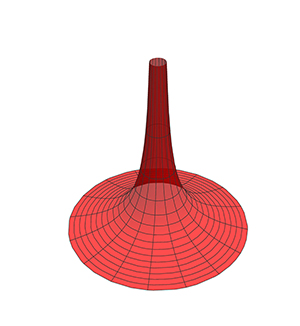
La trompette de Torricelli
La trompette de Torricelli, trompette de Gabriel ou cor de Gabriel, est une surface de révolution engendrée par une portion d’hyperbole. Mise en évidence par Evangelista Torricelli (1608–1647), cette surface possède la particularité d’enfermer un volume fini, bien que sa surface soit infinie. Torricelli l’a prouvé à l’aide de la méthode des indivisibles de Cavalieri, son maître, précurseur du calcul intégral. Elle a suscité une correspondance importante entre les mathématiciens de l’époque, qui ne connaissaient pas encore le calcul intégral.
