
On qualifie généralement de fractal tout objet présentant un aspect auto-similaire. Du chou romanesco aux motifs de certains coquillages, on ne compte plus les formes identifiées comme « fractales » dans la nature (voir les Fractales, Bibliothèque Tangente 18, 2019). Ces formes apparaissent souvent pour satisfaire des contraintes telles que l’optimisation de la surface d’échange entre l’intérieur et l’extérieur d’un organisme vivant.
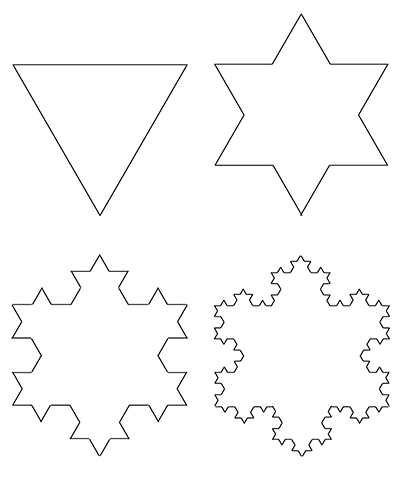
Premières étapes de la construction d’un flocon de von Koch (chaque segment est divisé en trois parties de même longueur ; le tiers médian est remplacé par deux segments de même longueur). Le flocon est la courbe limite, obtenue en itérant le processus à l’infini.
D’ordinaire, la modélisation mathématique de ces formes fractales produit des objets « rugueux », qui présentent des irrégularités à toutes les échelles. De telles surfaces sont tout sauf lisses. Parmi elles, on peut penser au classique flocon de von Koch, qui est une courbe qui ne ressemble pas à une droite même quand on la regarde de près : si proche qu’on se place d’elle, ses irrégularités nous font voir une ligne brisée.
Pour autant, le caractère rugueux des fractales n’est pas une fatalité : il est possible de rencontrer des surfaces à la fois fractales et lisses ! Ces dernières ont été récemment révélées lors de la résolution effective de deux sortes de contraintes géométriques apparemment sans lien : la compression d’une sphère dans le but de diminuer le volume qu’elle occupe ; et la représentation dans notre espace à trois dimensions d’une surface dont l’« habitat naturel » est un espace (euclidien) à quatre dimensions.
La Terre dans un dé à coudre
Le premier exemple de fractale lisse apparaît lorsque l’on cherche à « comprimer » une surface simple, par exemple une sphère, de manière à ce qu’elle enferme un volume plus petit. Pour illustrer cette contrainte, on peut imaginer que la surface terrestre est assimilée à une gigantesque sphère, que l’on cherche à nicher à l’intérieur d’un petit objet, par exemple… un dé à coudre. La difficulté est ici de déformer la sphère tout en préservant sa géométrie intrinsèque, c’est-à-dire les longueurs des courbes tracées à sa surface. Dit autrement : la distance de Grenoble (Isère) à Addis-Abeba (Éthiopie) doit être la même, qu’elle soit calculée à la surface de la terre ou sur la sphère déformée à l’intérieur du dé à coudre. La même propriété doit être satisfaite en remplaçant la ville française et la capitale éthiopienne par n’importe quels autres endroits du globe. Une telle surface déformée, isométrique à la sphère ordinaire, est appelée sphère réduite. À première vue, pareil objet ne saurait exister. Et pourtant…
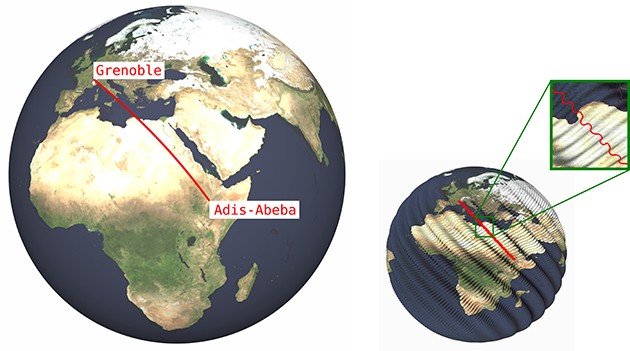
Globe terrestre isométrique à un globe terrestre réduit. Les distances entre les deux surfaces sont conservées.
Par exemple, la longueur du plus court chemin (tracé en rouge) entre Grenoble et Adis-Abeba est la même sur les deux surfaces.
Des résultats classiques de rigidité en géométrie montrent que la sphère réduite ne peut pas être « trop régulière ». Au milieu des années 1950, le célèbre mathématicien John Forbes Nash (1928–2015), héros du film biographique Un homme d’exception (Ron Howard, 2002), a cependant démontré l’existence de sphères réduites « lisses » (voir FOCUS). Au vu de l’impossibilité précédemment évoquée, le résultat contre-intuitif de Nash est apparu comme extraordinaire à son époque. La preuve de Nash ne menait cependant pas directement à une construction explicite.
Une vingtaine d’années plus tard, au milieu des années 1970, le non moins célèbre mathématicien Mikhaïl Gromov invente des outils mathématiques donnant un point de vue plus systématique sur les travaux de Nash.
Finalement, grâce aux outils développés par Gromov, une sphère réduite a pu être construite et visualisée en 2017 par l’équipe Hévéa (voir Tangente 178, page 10), plus de soixante ans après la démonstration théorique de son existence !
L’idée principale de la construction réalisée par l’équipe Hévéa, essentiellement constituée de chercheurs basés à Lyon (Institut Camille-Jordan et École normale supérieure de Lyon), Grenoble (Laboratoire Jean-Kuntzmann et Laboratoire Images, parole, signal, automatique) et Palaiseau (Laboratoire d’informatique de l’École polytechnique), est déjà de rétrécir la sphère terrestre en une sphère plus petite, suffisamment réduite pour tenir confortablement à l’intérieur du dé à coudre. Bien entendu, ce rétrécissement altère les longueurs des courbes, qui diminuent en proportion du rétrécissement ainsi opéré.
Dans une seconde étape, notre petite sphère est cette fois déformée, pour rallonger les longueurs des courbes définies à sa surface, tout en réussissant à ce que la nouvelle surface demeure à l’intérieur du dé à coudre. Pour cela, ce sont des « petites vaguelettes » qui sont ajoutées sur la sphère, un peu comme pour lui donner une forme de tôle ondulée. On parle parfois à leur sujet de corrugations (un terme introduit par Thurston dans le cadre du retournement de la sphère). Les courbes que l’on peut tracer sur cette sphère déformée suivent les oscillations des vaguelettes, et donc leur longueur change. En choisissant comme il convient l’amplitude et la fréquence de ces vaguelettes (leur hauteur et leur nombre par unité de longueur), il est possible de faire en sorte que les longueurs mesurées à la surface de cette sphère ondulée demeurent inférieures à celles mesurées à la surface de la Terre pour les points correspondants !
On répète ce processus de corrugations une infinité de fois, à chaque fois dans une nouvelle direction bien choisie, et en choisissant des amplitudes de plus en plus petites. La surface limite obtenue est une sphère réduite qui, si les paramètres de la construction ont été convenablement fixés, ne sera « pas trop irrégulière » (on la qualifiera donc de lisse), tout en tenant dans le dé à coudre et en étant isométrique à la sphère terrestre.
Sphère réduite isométrique à la sphère ordinaire. Ici, pour des raisons de précision de calcul, la sphère initiale est seulement réduite de moitié.

 Les trois premières étapes de la construction d’une sphère réduite :
Les trois premières étapes de la construction d’une sphère réduite :
une petite sphère (à gauche) sur laquelle on ajoute une, puis deux, puis trois séries de corrugations.
Une superposition de vaguelettes
L’accumulation infinie des corrugations conduit à un aspect fractal de la sphère réduite : à toute échelle on observe un même motif simple, une superposition de vaguelettes dans des directions variées. Ce caractère fractal peut paraître surprenant, puisque la sphère réduite est lisse. En général, la présence d’une autosimilarité, c’est-à-dire d’un même motif qui se répète à toutes les échelles, induit un aspect rugueux. Cependant, dans le cas de la sphère réduite, la répétition du motif de corrugations s’accompagne d’un aplatissement très rapide de ces dernières. Au fur et à mesure que l’on se rapproche de la surface, celle-ci semble « de plus en plus plate ». C’est cet aplatissement qui permet d’expliquer le caractère lisse de la surface limite.
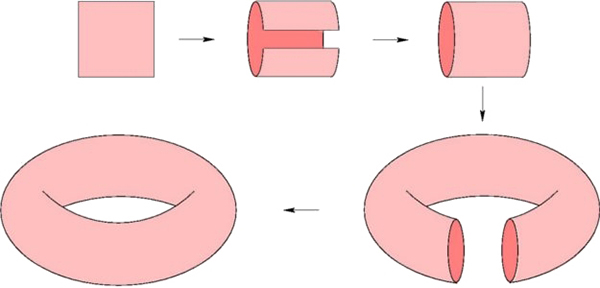
Le second exemple de fractale lisse provient de la visualisation dans notre espace à trois dimensions d’une surface qui vit naturellement dans l’espace à quatre dimensions : le tore carré plat. Le tore plat se définit classiquement comme un carré dont les côtés opposés sont identifiés deux à deux. À cause des identifications, ce tore ne peut pas être représenté dans le plan. Si l’on ne tient pas compte de la métrique, on le visualise en 3D par un tore de révolution (en forme de bouée). Mais il y a tromperie sur les distances ! Cependant, il en existe une représentation isométrique en quatre dimensions. Le problème, c’est qu’à moins d’être doté d’un « sixième sens » qui permette d’appréhender un espace quadridimensionnel, cette représentation ne permet pas de s’en faire une idée très concrète…
Tout comme pour la sphère réduite, il est possible de convoquer le théorème de Nash, qui nous indique que le tore carré plat peut se représenter isométriquement dans notre bon vieil espace à trois dimensions.
L’équipe Hévéa a construit une telle représentation par un procédé similaire à celui de la sphère réduite. Le principe est voisin : on part d’une version rétrécie du tore plat dans notre espace (en pratique, une petite bouée) et on applique une infinité de corrugations. Là encore, la surface obtenue présente un aspect à la fois fractal et lisse.

 Tore plat en 3D (vue extérieure et vue intérieure).
Tore plat en 3D (vue extérieure et vue intérieure).
Nature et fractales lisses
Les fractales lisses ont été découvertes en cherchant à résoudre des contraintes géométriques. La technique des corrugations, utilisée pour leur construction, intervient aussi dans la résolution d’autres problèmes géométriques tels le retournement de la sphère imaginé par le grand géomètre William Thurston (1946–2012). Ces corrugations sont plus généralement au cœur de la théorie dite de l’intégration convexe de Gromov, qui permet de résoudre toutes sortes de contraintes différentielles. On peut par ailleurs se demander dans quelle mesure les fractales lisses pourraient décrire certaines formes que l’on trouve dans la nature, à l’image des coques, qui semblent posséder deux niveaux de corrugations…
 Un cardiidae (mollusque bivalve).
Un cardiidae (mollusque bivalve).
Lire la suite