Le déclin d’Euclide

Si Gauss ne laisse que quelques notes et correspondances sur ses travaux par crainte des « cris de béotiens », le Hongrois János Bolyai (1802–1860), lui, n’hésite pas et rédige en 1829 un petit fascicule de vingt-quatre pages en latin (alors langue officielle en Hongrie), que son père Farkas incorpore à son œuvre maîtresse, le Tentamen. « De rien, j’ai construit un nouvel autre monde », écrit le jeune Bolyai à son père à seulement 21 ans. Un peu plus tard, et indépendamment, Nicolaï Lobatchevski (1792–1856) publie, en plusieurs textes, sa théorie des parallèles.

Chacune des trois grandes familles de langues européennes, slave, latine et saxonne, a donc participé à cette révolution, mais le russe et le hongrois eurent peu de lecteurs : ce n’est qu’à partir du remarquable travail de traduction et de communication du mathématicien français Jules Hoüel en 1866 que put enfin éclore la géométrie non euclidienne.

Les cartes de Beltrami

Dans un but cartographique, le mathématicien italien Eugenio Beltrami cherche, en 1865, à « reporter les points d’une superficie de manière à ce que les lignes géodésiques soient représentées par des droites ». Il découvre que la surface donnée doit être de courbure constante pour que le problème ait une solution, mais n’envisage que le cas d’une courbure positive.

En 1868, lorsqu’il prend connaissance de la géométrie non euclidienne via les traductions de Jules Houël, il publie enfin ses travaux, qui contiennent notamment ce qui est désormais connu sous le nom de représentation de Klein et de modèle de Poincaré. Sa gloire fut surtout d’avoir « tenté de trouver un substrat réel à [la] doctrine » des géométries non euclidiennes, en montrant explicitement une surface dans l’espace ordinaire (euclidien) sur laquelle faire de la géométrie où le postulat d’Euclide n’est plus valable. La surface en question est la pseudosphère, une surface dont Ferdinand Minding avait démontré en 1839 être de courbure constante négative.

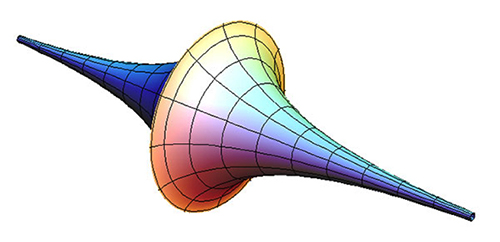
La pseudosphère.

Le disque de Poincaré

Eugenio Beltrami souligne à plusieurs reprises que ses modèles non euclidiens (voir ci-dessous) ne sont en quelque sorte que des « effets collatéraux » de ses recherches sur les surfaces. C’est le mathématicien français Henri Poincaré (1854–1912) qui saura tirer tout le parti géométrique possible des idées de Beltrami. Poincaré n’a donc pas « inventé » le disque qui porte son nom, mais il est celui qui en a exploré toute la richesse en expliquant que ce nouveau monde n’est « ni contradictoire ni inimaginable ».

Les « droites » du disque de Poincaré sont les arcs de cercle orthogonaux à la circonférence du disque, ainsi que les diamètres du disque. Toutes les propriétés de la géométrie classique, dans lesquelles le mot « droite » se voit attribué ce nouveau sens, sont également satisfaites dans le monde du disque de Poincaré… sauf bien sûr le cinquième postulat d’Euclide et ce qui en découle. Le disque de Poincaré offre ainsi une fenêtre vers un nouveau monde non euclidien.

Pavage « triangulaire »
du disque de Poincaré.