« Alice se mit à rire.  “Inutile d’essayer, répondit-elle : on ne peut absolument pas croire des choses impossibles.

– Je suppose que tu manques d’entraînement, répondit la Reine. Quand j’avais ton âge, je m’y exerçais une demi-heure par jour. Il m’est arrivé quelquefois de croire jusqu’à six choses impossibles avant le petit déjeuner. Voilà mon châle qui s’en va de nouveau !” »

Lewis Carroll, De l’autre côté du miroir, 1871

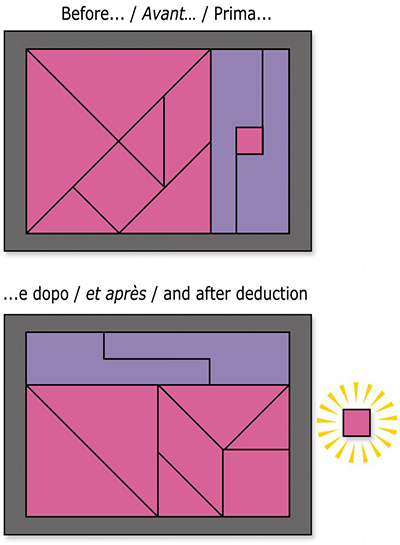
Parmi les innombrables énigmes et paradoxes, le classique suivant est sans doute le plus impossible à croire. On vous donne un échiquier sans couleurs, constitué de soixante-quatre carrés et divisé selon les lignes épaisses représentées ci-contre. Il s’agit de reconstituer les quatre pièces en rectangle.

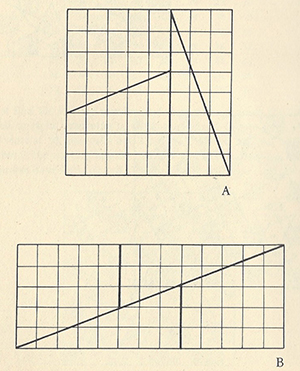
Un compte rapide des petits carrés, de côté et d’autre du rectangle, donne 5 et 13. La surface se constitue donc forcément de soixante-cinq carrés, ce que l’on peut vérifier en comptant individuellement les carrés. D’où est venu le carré supplémentaire ?

Un interstice invisible à l’œil nu

Si l’échiquier est construit avec précision, le rectangle va finalement ne pas posséder une diagonale précise : il va subsister un interstice, que l’épaisseur du trait de crayon va masquer et qui va donc passer inaperçu. La surface de l’espace emprisonné « le long de la diagonale » est équivalente à celle du mystérieux carré.

Lewis Carroll (1832–1898), auteur à succès avec les Aventures d’Alice au pays des merveilles et mathématicien professionnel sous son vrai nom Charles Lutwidge Dodgson, a généralisé ce paradoxe dans une équation qui produit les dimensions de tous les carrés possibles qui peuvent être disséqués de la même façon (on obtient ainsi des « carrés supplémentaires » avec un échiquier de côtés 21 et 55 par exemple). Le paradoxe est décrit de façon exhaustive par le mathématicien américain Warren Weaver dans The American Mathematical Monthly en avril 1938, à partir de notes incomplètes de Carroll datant de la période 1890–1893. Il est également inclus par Stuart Dodgson Collingwood, le neveu du « père » d’Alice, dans le Lewis Carroll Picture Book.

Il est peu probable cependant que Carroll soit l’inventeur du problème. Dans son Cyclopedia of Puzzles, le créateur de casse-tête américain Sam Loyd (1841–1911) prétend l’avoir présenté à l’American Chess Congress en 1858, en le décrivant ultérieurement comme étant l’ancêtre de son puzzle Get Off The Earth (« Quitter la Terre »), breveté en 1896. On se demande cependant pourquoi Loyd relie ses deux créations qui ne sont pas basées sur le même principe… En effet, dans le paradoxe géométrique, le découpage et la recomposition du quadrilatère ne fait rien disparaître mais crée seulement un vide invisible à l’œil nu.

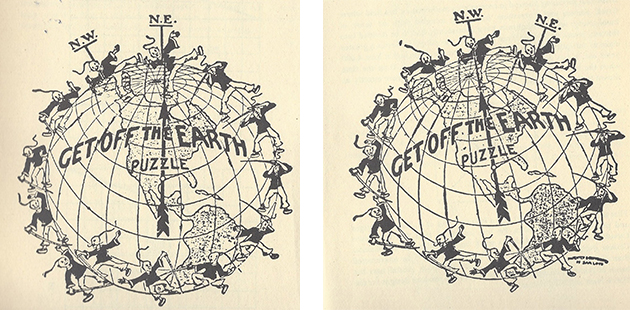
Le découpage de Get Off The Earth, en deux morceaux seulement, suivi d’une rotation, fait disparaître l’un des personnages, qui est en fait « partagé » et redistribué sur les autres.

Quand 64 = 63…

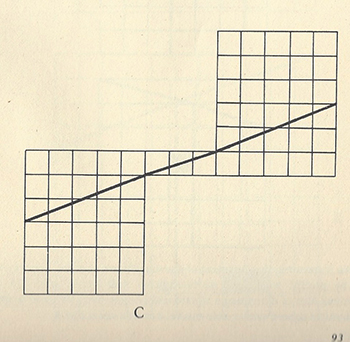
Le fils de Sam Loyd fut le premier à découvrir que les quatre pièces du puzzle géométrique initial peuvent également être reconstituées pour former une surface réduite à soixante-trois carrés !

Le très créatif magicien américain Paul Curry a mis au point, en 1953, un développement intéressant de ce paradoxe de l’échiquier, avec l’ingénieuse idée de découper un carré en cinq morceaux puis de les rassembler pour reconstituer le carré initial… mais avec un trou intérieur.

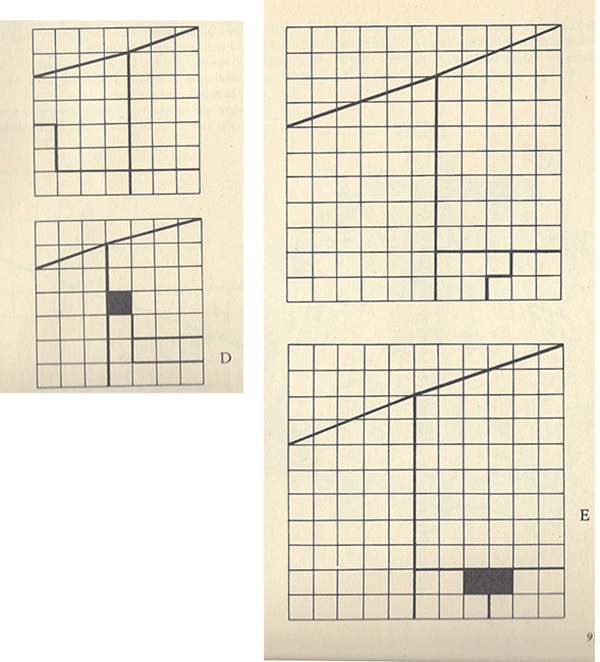
Mais ni Carroll, ni les Loyd n’ont fait état de la suite de Fibonacci, qui régit pourtant in fine les dimensions des quadrilatères permettant le paradoxe. Tout en créditant Loyd de sa découverte, le célèbre vulgarisateur américain Martin Gardner (1914–2010) nommera d’ailleurs paradoxe de Fibonacci ce type de disparition, qui fera florès dans la création de casse-tête contemporains.

En effet, les dimensions des figures mentionnées relèvent des propriétés de la suite de Fibonacci, dont chaque terme est égal à la somme des deux précédents : 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89… Or, dans cette suite, le carré de chaque terme est égal au produit des termes qui l’encadrent, plus ou moins 1. Ainsi, 8² = 5 × 13 – 1, 13² = 8 × 21 + 1, ou encore 21² = 13 × 34 – 1. Il suffit donc de découper un carré, construit avec un côté correspondant à un nombre F_n de la suite de Fibonacci, et de reconstruire avec les morceaux obtenus un rectangle de taille F_n–1 par F_n+1. Ce choix de termes alternés entraîne un ajustement imparfait le long de la diagonale du rectangle avec un gain apparent d’un petit carré unité. L’ajustement apparent (interstice ou recouvrement) est d’autant moins visible que le terme choisi pour le côté est grand.

De nombreuses généralisations du paradoxe ont été tentées en variant les découpes ou en utilisant d’autres suites, inspirées de celle de Fibonacci. Ainsi, avec la suite 1, 4, 5, 9, 14…, on perd onze carrés unitaires en passant d’un carré 9 × 9 à un rectangle 5 × 14. Plus récemment, Gianni Sarcone (www.giannisarcone.com), bien connu des lecteurs de Tangente, a créé depuis 1992 des puzzles allant de trois (seulement !) à douze pièces, dont les découpages eux-mêmes sont souvent liés au nombre d’or, qui apparaît naturellement dans la suite de Fibonacci (comme limite des quotients de deux termes consécutifs de la suite).

  Le TangraMagic de Gianni Sarcone.