L’ordre de grandeur de la taille d’un virus est celui du nanomètre, c’est-à-dire du milliardième de mètre (1 nm = 10 ^–9 m), ou encore du millionième de millimètre. On réussit aujourd’hui à visualiser des particules virales dans un échantillon clinique, ou dans des cellules infectées, à l’aide de microscopes. Ceux-ci révèlent, outre la forme parfois très étrange de certains virus, les « trous » que ceux-ci peuvent faire dans une couche de bactéries. On parle de plages de lyse ; elles sont formées par des bactériophages, ou phages, donc par des virus capables d’infecter des bactéries, de s’y multiplier et de les dissoudre.

L’étendue d’une plage de lyse est notamment liée au pouvoir de multiplication des virus. Il est donc utile de pouvoir calculer l’aire de telles régions, qui ont la double caractéristique d’être microscopiques et d’avoir un contour qui peut se révéler fort tortueux.

Le principe de base pour résoudre un tel problème consiste à estimer l’aire d’une plage de lyse à l’aide de celle d’un polygone dont les sommets sont situés sur le contour extérieur de la plage. Bien entendu, l’approximation ainsi faite est d’autant plus précise que le nombre de points retenus est élevé.

Des maths en blouse blanche

En pratique, l’opération peut s’effectuer à l’aide d’un matériel peu sophistiqué, courant dans les laboratoires spécialisés : un ordinateur couplé à une table numérique, elle-même couplée à un microscope classique.

Grâce à un jeu de miroirs, la plage observée à l’aide du microscope apparaît sur la table digitale, à une échelle fixée par l’utilisateur. À l’aide d’un crayon magnétique, l’expérimentateur recopie le contour extérieur de la plage. Le contact du crayon et de la table détermine les coordonnées cartésiennes réelles de points du contour (par exemple, au rythme d’environ soixante points par seconde, cela donne habituellement plusieurs centaines de points). Les coordonnées des points sont alors transmises à l’ordinateur.

C’est ensuite que les mathématiques entrent en scène, pour calculer l’aire voulue à partir des coordonnées des points ainsi déterminés.

La courbe qui délimite la plage de lyse est parcourue dans le sens trigonométrique ou positif (c’est-à-dire dans le sens inverse des aiguilles d’une montre). On y repère successivement, et dans l’ordre de leur rencontre, n points définissant un polygone. Notons P₁, P₂… P_n ces points. Les coordonnées du point P_i sont ( x_i, y_i), dans un repère cartésien préalablement fixé. On fixe enfin par commodité la convention de définir le point P_n +1 comme étant égal au point P₁, si bien que l’on a x_n+1 = x₁ et y_n+1 = y₁.

L’aire approchée A de la plage de lyse est alors donnée par la formule suivante :

\( \text{A} = \dfrac{1}{2} \displaystyle\sum_{i=1}^{n} \mid x_i y_{i+1} - x_{i+1}y_i\mid.\)

Pour la justifier, on peut utiliser un résultat élémentaire relatif à l’aire T d’un triangle de sommets P₁, P₂ et P₃ : celle-ci est égale à la moitié de celle du parallélogramme construit à partir des vecteurs  \( \overrightarrow {\text{P}_1 \text{P}_2}\) et  \( \overrightarrow {\text{P}_2 \text{P}_3}.\)

On en déduit que, au signe près, 2T est égal à la norme du produit vectoriel de ces deux vecteurs, ce qui donne la formule suivante :

2T = |( x₂ –x₁)( y₃ –y₂) – ( y₂ –y₁)( x₃ –x₂)|,

de laquelle on tire immédiatement :

T = |( x₁y₂ + x₂y₃ + x₃y₁) – ( x₂y₁ + x₃y₂ + x₁y₃ )| / 2.

La géométrie des polygones

Le résultat particulier obtenu pour A = T (l’aire d’un triangle) permet ensuite d’atteindre le cas général dans lequel les n points choisis sur le bord de la plage sont les sommets d’un polygone convexe. En effet, choisissons dans ce cas un point P₀, de coordonnées ( x₀, y₀), situé à l’intérieur du polygone. On constate alors que l’aire polygonale que nous recherchons est simplement égale à la somme des aires T_i des n triangles successivement définis par les sommets P₀, P_i et P_i+1.

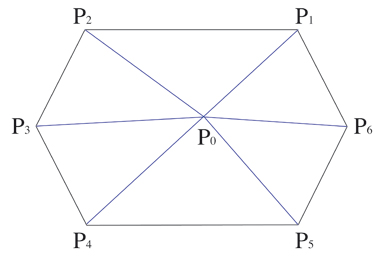
Partage d’un polygone (ici n = 6) en triangles. 
 L’aire de l’hexagone est égale à la somme des aires des six triangles ayant P₀ comme sommet commun.

La convention fixée consistant à identifier P_n+1 à P₁ permet alors d’écrire la suite d’égalités suivante :

  \( \text{A} = \displaystyle\sum_{i=1}^{n} \text{T}_i = \dfrac{1}{2} \displaystyle\sum_{i=1}^{n} \mid (x_0 y_i + x_iy_{i+1} + x_{i+1}y_0) - (x_i y_0 + x_{i+1} y_i + x_0 y_{i+1}) \mid \)

et donc, après développement et simplification :

\( \text{A} = \dfrac{1}{2} \displaystyle\sum_{i=1}^{n} \mid x_i y_{i+1} - x_{i+1}y_i\mid,\)

qui est la formule cherchée.

Cette méthode (et la formule qui en découle) est encore valable dans un cadre plus général, notamment lorsque le polygone approchant la plage de lyse est un ensemble non nécessairement convexe mais seulement expansé, c’est-à-dire qu’il contient un point P₀ pour lequel, quel que soit le point P à l’intérieur du polygone, le segment limité par P₀ et P est tout entier dans le polygone. On dit encore que le polygone est étoilé par rapport au point P₀.

Un polygone convexe n’est qu’un exemple de polygone expansé ; une forme « en étoile » est un exemple de polygone expansé non convexe.

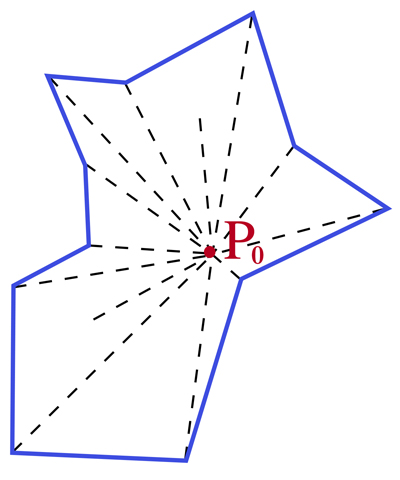
Un exemple de polygone étoilé non convexe.

La formule permettant le calcul de l’aire A délimitée par la plage de lyse s’étend à des cas encore plus généraux. En effet, les lignes polygonales ne sont pas toujours les plus adaptées pour matérialiser le contour de A : il faut alors pouvoir remplacer des segments de droite par des courbes plus générales. On obtiendra donc une surface plus élaborée qu’un polygone. Les mathématiques permettent heureusement d’envisager de telles généralisations. Une célèbre formule, dite de Green–Riemann, permet dans de telles situations d’exprimer l’aire cherchée à l’aide d’une intégrale curviligne.

Modèle polygonal de Low du virus de l’hépatite B.