À la suite des paradoxes de Zénon, les anciens Grecs s’interdirent le recours à l’infini en ne le concevant, tout comme Aristote, que comme potentiel : on peut partager un segment en morceaux de plus en plus petits, sans que l’opération mentale n’ait de fin théoriquement assignable mais sans jamais pourtant que l’on puisse matériellement la prolonger effectivement à l’infini.

Le recours à l’infini actuel, c’est-à-dire un infini présent « pour de bon », revint en grâce bien plus tard, notamment sous l’impulsion de Bonaventura Cavalieri (1598–1647) et sa méthode des indivisibles qu’il exposa dans Geometria indivisibilibus continuorum nova quadam ratione promota publié en 1635. Celle-ci était cependant déjà utilisée par Gilles Personne de Roberval, comme le Français l’a rappelé en juin 1647 dans une lettre à Evangelista Torricelli (1608–1647, voir FOCUS).

Roberval a utilisé cette méthode pour étudier l’aire sous une arche de cycloïde, cette courbe « star » de l’époque qui a donné aux mathématiciens l’occasion de dépasser les théorèmes de la géométrie classique et de préparer l’avènement du calcul infinitésimal.

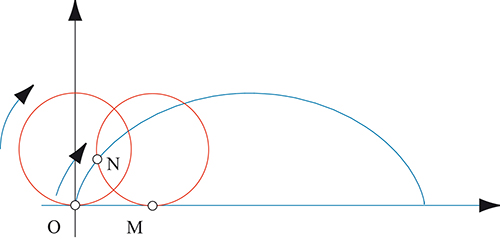
Parce que la roue roule sans glisser, les longueurs OM (mesurée positivement à droite de O) et MN (mesurée sur le cercle tangent au sol en M) sont égales.

Quarrer la cycloïde

 La cycloïde est la courbe que décrit un point d’une roue qui roule (sans glisser) sur une ligne droite. Cette courbe fut l’objet de nombreux défis au cours du XVII^e siècle.

Pour estimer l’aire d’une arche d’une cycloïde (c’est-à-dire, sur le schéma, de la surface délimitée par l’axe horizontal et la cycloïde bleue), Galilée (1564–1642) en avait fabriqué une en zinc et l’avait pesée pour en estimer l’aire. Cette mesure expérimentale l’avait conduit à penser que l’aire de l’arche de la cycloïde était le triple de celle du cercle à partir duquel elle était construite. Il ne réussit pas à le démontrer, et c’est finalement Roberval qui y parvint, grâce, donc, à la méthode des indivibles. 

Roberval commence par définir une courbe auxiliaire, qu’il nomme la compagne de la cycloïde, en reportant les segments [AB] du cercle initial en [CD] le long de la cycloïde. Il remarque que cette courbe est symétrique par rapport au centre du rectangle. L’aire en orange sous la compagne de la cycloïde est donc la moitié de celle du rectangle, soit πR², l’aire du cercle générateur.

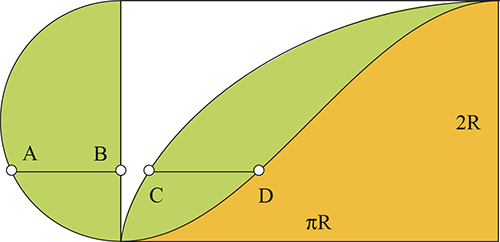
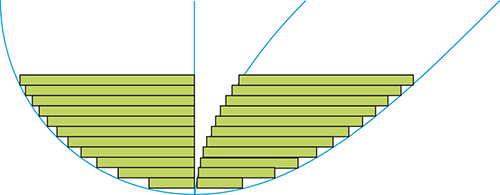
D’autre part, la méthode des indivisibles lui permet d’affirmer que l’aire entre la cycloïde et sa compagne est égale à l’aire du demi-cercle, car les deux zones sont engendrées par des segments parallèles et de même longueur. C’est ainsi qu’il retrouve le résultat conjecturé par Galilée : l’idée sous-jacente est que l’on retrouve deux fois la même somme de petits rectangles, comme le montre la figure suivante.

Les différentielles de Leibniz

Malgré le succès de Roberval pour la cycloïde, la méthode des indivisibles a vite montré ses limites. L’un de ses principaux défauts était de ne pas pouvoir s’adapter à toutes les situations. Pour calculer l’aire d’une surface limitée par une courbe, il fallait déployer des trésors d’ingéniosité.

Quelques années plus tard, c’est Leibniz qui effectue la percée tant attendue, en introduisant une notion générale quelque peu déroutante : celle d'accroissement infinitésimal d’une variable, qui généralisait l’idée des indivisibles. Si x était une quantité variable, le mathématicien allemand note dx un accroissement infinitésimal de cette quantité. Si une quantité y dépend de x, par exemple y = x², alors dy = (x + dx)² - x². Les deux termes dx et dy sont appelés différentielles  (dx est celle de x, et dy celle de y). En développant le carré de x + dx, cette égalité se simplifie en dy = 2x dx + (dx)². Arrivé à ce point, Leibniz affirme que le terme (dx)² est négligeable devant 2x dx, au point de le considérer comme nul, d’où dy = 2x dx.

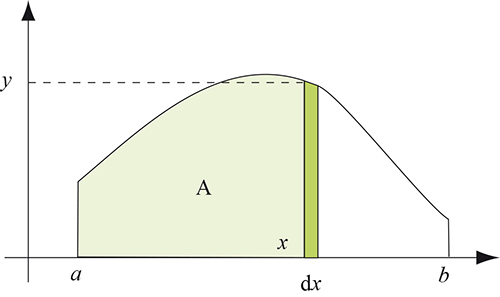
Bien entendu, de telles opérations manquent de rigueur : une quantité est nulle ou ne l’est pas, elle ne peut l’être quand on le désire et ne plus l’être en d’autres occasions ! Un gros travail fut nécessaire pour comprendre en quoi ce genre d’abus n’empêchait pas la théorie de fonctionner. Le jeu en valait la chandelle, car les différentielles de Leibniz permettent d’envisager les calculs d’aires d’une façon considérablement plus générale que les méthodes anciennes. Soit en effet un domaine délimité par une courbe d’équation y = y(x) > 0 pour x variant entre deux bornes a et b. Si l’on note A = A(x) l’aire entre les bornes a et x, on montre que dA = y dx et que l’aire totale est la somme de ces rectangles y dx, ce que l’on note aujourd'hui

  \( \int_{a}^{b}y\, dx\)  

(jusqu’au XVIII^e siècle, on employait la lettre « s »).

Avec cette méthode, il suffit de connaître des équations paramétriques de la cycloïde pour en déduire l’aire. Si R est le rayon du cercle, alors x = R(t – sin t), y = R (1 – cos t), l’aire A_cycl est égale à l’intégrale de 0 à 2π de y dx, soit :

\( {\rm A}_{cycl}\int_{0}^{2\pi}(1-\cos t)^2dt=3\pi {\rm R}^2.\)

Le calcul est plus abstrait, mais son avantage incomparable est qu’il n’y a plus vraiment besoin d’ingéniosité particulière, telle que celle dont Roberval avait fait montre. Pour évaluer l’aire sous la cycloïde, un calcul systématique suffit ! C’est la puissance irremplaçable du calcul intégral moderne.