B.R. : Le titre de votre livre affirme que la Terre ne tourne pas rond, mais rassurez-nous : elle est bien ronde, quand même ?
X.C. : Disons qu’elle est « presque ronde » ! On sait depuis Newton que la surface de la Terre est mieux décrite par un ellipsoïde de révolution, c’est-à-dire une ellipse que l’on fait tourner autour de son petit axe. Notre planète a un bourrelet à l’équateur, mais en première approximation on peut sans problème la regarder comme sphérique.

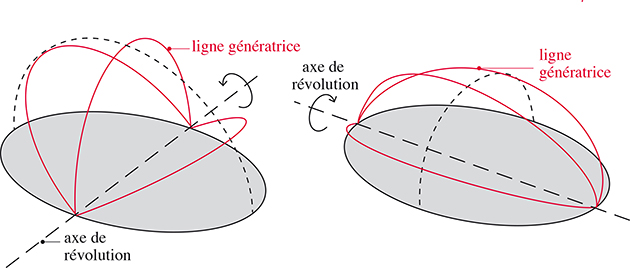
L’ellipsoïde de révolution est obtenu en faisant tourner une ellipse autour de l’un de ses deux axes.

Quand a-t-on compris que la Terre ressemblait à une sphère ?
Il y a un malentendu fréquent sur cette question. Beaucoup de gens croient, à tort, que l’on pensait la Terre plate avant l’époque moderne : c’est complètement faux, toutes les personnes cultivées savaient très bien et depuis fort longtemps que la Terre est ronde. Les traces écrites de cette idée remontent à la Grèce ancienne. Les pythagoriciens, ainsi que Platon, proposent déjà l’idée d’une Terre ronde, même s’ils le défendent avec des arguments qui ne sont pas convaincants pour un physicien d’aujourd’hui. Aristote en revanche, au IV^e siècle avant notre ère, donne un argument décisif : il constate que lors d’une éclipse de Lune, l’ombre portée de la Terre sur notre satellite est courbée comme un cercle. Il en déduit la rotondité de la Terre. Aristote signale aussi (mais on ignore si cet autre argument est de lui) qu’un bateau semble s’enfoncer sous l’horizon lorsqu’il s’éloigne, ce qui démontre d’une autre manière le caractère courbe de notre planète.

La mesure de la Terre

D’où vient alors ce mythe de la Terre plate ?
On trouve dans la Bible, ainsi que dans le Coran, un ou deux passages qui, pris au pied de la lettre, suggèrent que la Terre est une surface plate. Lactance, un père de l’Église, l’affirme même explicitement. Toutefois, dans tous les milieux instruits de l’époque médiévale on sait parfaitement à quoi s’en tenir. Il suffit d’ailleurs de se référer aux multiples représentations de Dieu soutenant le monde : la Terre y est toujours représentée comme une sphère.

Et sa taille ?
La première mesure de la circonférence de la Terre a été faite par Ératosthène, un savant grec du III^e siècle avant notre ère. En un mot, l’idée d’Ératosthène consiste à mesurer la portion de méridien (une ligne qui joint les pôles à la surface du globe) entre deux points et, à l’aide de mesures astronomiques, de déterminer l’angle que ces deux points font avec le centre de la Terre. Si la distance mesurée vaut d et l’angle a (en degrés), alors la circonférence de la Terre est de d × (360 / a). C’est extraordinairement simple, mais en pratique il était difficile à Ératosthène d’être précis dans ses mesures.

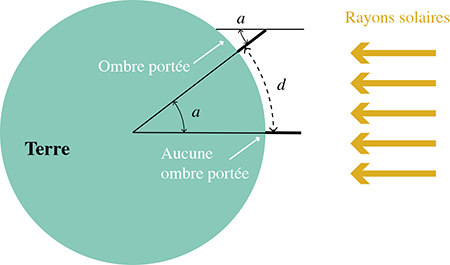
Pour cette expérience, les rayons solaires sont supposés parallèles.

Il s’est trompé de beaucoup ?
Il a fait mieux que donner le bon ordre de grandeur, mais il ne faut pas lui prêter plus qu’il ne pouvait faire. Un problème pour reconstituer son résultat est qu’il le donne en stères, une unité de mesure de l’époque qui était définie de manière très diverse selon les régions. Si l’on veut à tout prix dire qu’Ératosthène a été très précis, il suffit de choisir la définition qui produit le résultat « le plus proche de la réalité »…

La mesure faite par Ératosthène a-t-elle fait référence ?

C’est là qu’elle a cessé d’être parfaitement ronde ?
Newton s’est posé la question un peu par hasard, en cherchant à comprendre l’un des mouvements de la Terre. En plus des mouvements de rotation autour de son axe (qui cause l’alternance des jours et des nuits) et de révolution autour du Soleil (qui cause l’alternance des saisons), l’orientation de l’axe de la Terre n’est pas fixe : il tourne au fil du temps, et revient à sa position initiale en environ vingt-six mille ans : c’est la précession des équinoxes, connue depuis l’Antiquité et ainsi nommée parce qu’on l’observe en constatant que la position du Soleil au moment de l’équinoxe de printemps (ou d’automne) avance d’une année sur l’autre.

En quoi cela est-il lié à la forme de la Terre ?
Newton a compris que la précession des équinoxes devait s’expliquer par un défaut de sphéricité de la Terre. Comme son axe de rotation n’est pas exactement perpendiculaire au plan de son orbite, le fait que la Terre soit renflée à l’équateur fait que le Soleil exerce sur elle une attraction différenciée qui permet d’expliquer les mouvements de son axe de rotation. De façon étonnante, la forme de la Terre détermine donc l’un de ses mouvements.

 

Le rôle de l’attraction terrestre

Pourquoi cela a-t-il créé une polémique ?
Face à Newton, il y avait les cartésiens et la majorité de l’Académie des sciences de Paris, dont les idées sur les fondements de la physique s’opposaient à la théorie de la gravitation universelle. Les cartésiens penchaient, eux, pour une Terre amaigrie à l’équateur, donc en forme de ballon de rugby avec les pôles pour extrémités. Finalement, l’Académie des sciences a envoyé deux expéditions pour faire des mesures, l’une à l’équateur et l’autre en Laponie. C’est ce qui a permis de trancher la question une fois pour toutes en faveur de Newton. C’est aussi lors de ces expéditions que l’on a commencé à s’intéresser aux variations de l’attraction terrestre selon le lieu, en constatant qu’un pendule oscille plus lentement à l’équateur qu’à Paris, parce que la surface terrestre à l’équateur est plus éloignée du centre de la Terre.

Qu’en est-il des autres planètes ?
Les planètes du système solaire ne sont pas parfaitement sphériques, même si leur défaut de sphéricité est variable. On sait aujourd’hui mesurer l’aplatissement planétaire avec grande précision. On le définit comme le rapport (R_E – R_P) / R_E, où R_E désigne le rayon équatorial et R_P le rayon polaire. En voici les valeurs pour chaque planète : Mercure : 0, Vénus : 0, Terre : 0,0033529, Mars : 0,00589, Jupiter : 0,06487, Saturne : 0,09796, Uranus : 0,02293, Neptune : 0,0171.
Comme on le voit, la planète « la plus aplatie » est Saturne. On peut d’ailleurs constater visuellement son aplatissement même avec un télescope modeste ! La structure gazeuse de Jupiter, Saturne, Uranus et Neptune explique leur aplatissement plus important que celui des planètes solides (telluriques) que sont Mercure, Vénus, la Terre et Mars, les deux premières n’étant pas loin de sphères géométriquement parfaites.

Se pose donc alors la question d’une autre manière de considérer la surface de la Terre, une manière abstraite : les points où l’attraction s’exerce de la même manière.
Il est difficile de trouver le fil conducteur historique de cette question, dont on commence à parler principalement à partir des années soixante-dix. On définit alors le géoïde, une enveloppe virtuelle de la planète où l’attraction terrestre est la même en chaque point. On peut voir l’apparition de ce concept comme un effet de la mondialisation de la fin du XX^e siècle : auparavant, chaque État avait ses cartes et ses conventions, telles que celles qui définissaient l’altitude 0. En France, par exemple, c’était le niveau de la mer à Toulon (Var). Apparaît alors la nécessité d’un point de vue unifié, « global » dans les deux sens du terme.

Pour quelles raisons concrètes ?
Il y a la question du lancement des satellites artificiels en orbite autour de la Terre, mais aussi des considérations militaires, pour la conception de missiles intercontinentaux. L’armée américaine s’est beaucoup impliquée dès les premières études sur le géoïde. Les hydrologues s’intéressent aussi à la question : comprendre les variations, même faibles, de l’attraction terrestre selon le lieu est utile pour étudier les grands bassins versants.

Quelle est la forme du géoïde ?
Autant la forme visible de notre planète, que l’on appelait joliment à la Renaissance la « figure de la Terre », peut plaire aux mathématiciens qui y retrouvent une forme connue (l’ellipsoïde), autant le géoïde est une surface unique bien éloignée de l’élégance géométrique traditionnelle. Le géoïde est une déformation de l’ellipsoïde, avec des creux et des bosses un peu partout, qui reflètent les irrégularités de la matière terrestre. Les choses sont parfois subtiles : par exemple, on s’attendrait à ce qu’au-dessus d’une montagne le géoïde « monte » avec elle. Or ce n’est pas toujours le cas, si le socle de la montagne est d’un matériau moins dense.

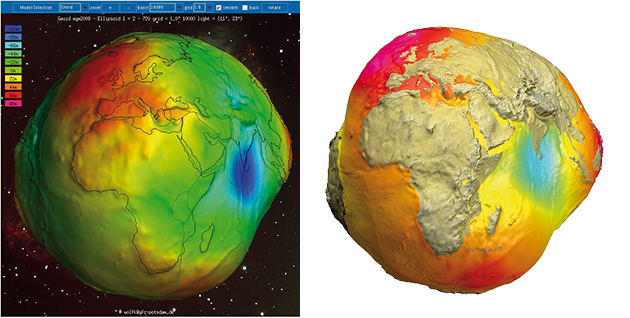Le géoïde.

Des applications locales concrètes

Le géoïde est-il si différent de l’ellipsoïde terrestre ?
Il y a autant de choix théoriques possibles pour le géoïde qu’il y a de choix possibles pour une surface sur laquelle l’attraction terrestre est constante. En pratique, on choisit celle qui « colle au plus près » à la forme physique de la Terre, et la différence entre les deux ne varie jamais plus d’une centaine de mètres d’altitude. Pour visualiser les différences sur un graphique, on est amené à appliquer un facteur d’échelle énorme par rapport à la réalité.

Depuis les années soixante-dix, y a-t-il eu d’autres applications que les emplois militaires ou hydrologiques ?
La principale application courante du concept est le GPS. Il se trouve en effet que les variations de l’attraction terrestre exercent un effet mesurable sur la position des satellites qui font les mesures. Connaître tout cela avec grande précision est nécessaire pour être capable de disposer d’un système de positionnement fiable à l’échelle du centimètre, une échelle qui doit permettre quantité d’applications nouvelles comme la mesure de terrains, ou même d’appartements. La forme de la Terre et de son géoïde a donc désormais des applications potentielles aussi à l’échelle la plus locale.

Xavier Campi est directeur de recherches honoraire au CNRS.
Il a mené une carrière en physique théorique sur le site de l’université Paris-XI. Il se consacre aujourd’hui à la diffusion de la connaissance scientifique. Il est l’auteur de l’ouvrage la Terre ne tourne pas rond (Cassini, 2014).