L’une des grandes affaires mathématiques de la Renaissance est l’introduction de la perspective. Cette révolution correspond, entre autres, à la conjonction de plusieurs préoccupations et progrès techniques : la disponibilité de copies des Éléments d’Euclide, base de la géométrie ; un essor artistique ; la volonté de réconcilier Platon, auteur très en vogue à la Renaissance, avec les représentations artistiques ; l’arrivée de vitres et vitraux de grandes surfaces.

Les Éléments d’Euclide traitant aussi des polyèdres, leur étude va reprendre, et on va même les dessiner et les reproduire. Une pratique artisanale de l’époque va jouer un rôle, celle de l’intartia. Il s’agit de panneaux de bois en marqueterie représentant (évidemment en perspective) ce que le panneau est censé cacher. Pour montrer leur virtuosité, les artisans vont figurer des polyèdres, au départ ceux des Éléments, puis des objets plus sophistiqués. Dans les ateliers où l’on travaille le bois, ces mêmes artisans vont aussi certainement chercher à construire physiquement ces polyèdres, pour vérifier la validité de leurs dessins. L’un des acteurs de cette époque est Piero della Francesca, qui rédige les premiers traités sur la perspective… et aussi sur les polyèdres. Malheureusement, il n’a pas publié de son vivant.

Du côté de la géométrie

Le plus grand mathématicien de l’époque est sans doute le moine Luca Pacioli. En 1494, il publie son chef-d’œuvre à Venise : Summa de arithmetica, geometria, proportioni et proportionalita. En 1496, le duc de Milan, Ludovic Sforza, l’invite à Milan pour enseigner les mathématiques dans les écoles du palais. Là, il rencontre Léonard de Vinci et lui enseigne la géométrie, en lui faisant accéder aux Éléments d’Euclide, car Léonard maîtrise mal le latin. Les deux hommes deviennent amis ; ils partent ensemble en 1499 vers Mantoue. Mais à Milan, entre 1496 et 1498, Pacioli compose le célébrissime De divina proportione, qui ne sera publié qu’en 1509 à Venise.

Cet ouvrage possède un statut très particulier dans l’histoire de l’imprimerie. Il est écrit en langue vulgaire. Dans la première partie, Compendio de divina proportione, il expose les propriétés du nombre d’or et de soixante types de polyèdres. Suivent les planches réalisées par Léonard. Enfin, une version italienne d’un ouvrage de Piero della Francesca conclut l’ouvrage. Le problème est que Pacioli ne cite jamais della Francesca, qui est décédé à cette époque. Il a d’ailleurs été accusé de plagiat pour cette publication ! A-t-il voulu faire connaître l’œuvre de della Francesca, qui n’a jamais été publiée de son vivant ?

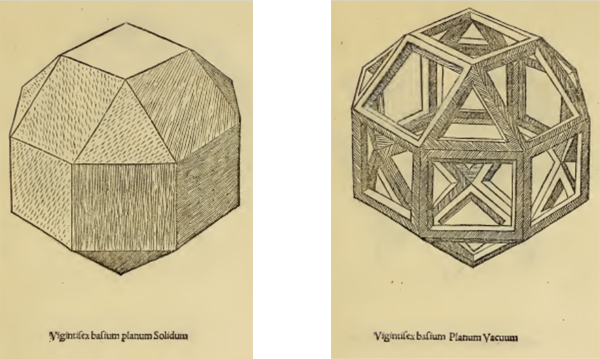
À gauche : Le petit rhombicuboctaèdre, forme planus.

À droite : Le petit rhombi-cuboctaèdre, forme vacuus.

Un autre point est que les planches de Léonard en disent beaucoup plus que le texte de Pacioli. Ce n’est pas surprenant : à cette époque, l’expression graphique est un moyen d’expression privilégié. Là, les prodigieuses illustrations de Léonard ont beaucoup contribué au succès de l’ouvrage, ce que Pacioli admet volontiers. C’est d’autant plus étonnant qu’à l’époque Léonard est… l’élève de Pacioli ! Ainsi, De divina proportione est le premier livre imprimé où l’illustrateur est bien meilleur que l’auteur…

Les solides décrits dans l’ouvrage sont essentiellement des polyèdres ; on rencontre aussi la sphère, le cône et le cylindre. Les polyèdres sont décrits sous deux formes : la forme planus, « pleine », comme si le polyèdre était taillé dans un bloc, et la forme vacuus, comme si l’on matérialisait les arêtes par des barreaux de bois, ce qui laisse l’intérieur du polyèdre vide et permet ainsi de voir sa structure interne. Très spectaculaire, cette représentation est entrée dans nos mémoires. En 1597, Kepler, qui n’a vraisemblablement pas eu accès au De divina proportione, l’emploie lui aussi pour ses polyèdres dans son Mysterium Cosmographicum.

À gauche : Le petit rhombicuboctaèdre étoilé, forme planus. 
À droite : Le petit rhombicuboctaèdre étoilé, forme vacuus.

De plus, Léonard présente systématiquement une forme elevatus : sur chaque face des polyèdres décrits, il somme une pyramide dont les faces latérales sont des triangles équilatéraux. C’est une nouvelle forme de génération de polyèdres, qui préfigure l’étoilement cher à Kepler. Ces polyèdres « étoilés » sont à nouveau déclinés sous les deux formes planus et vacuus.

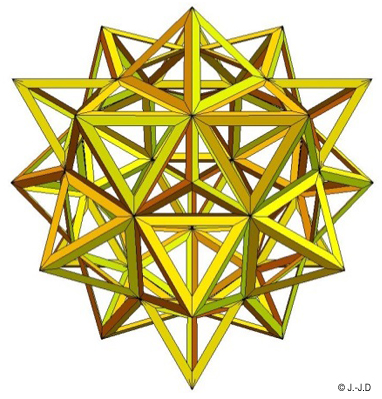
Le petit rhombicuboctaèdre étoilé.

Les polyèdres exhibés sont les cinq solides platoniciens et quelques polyèdres archimédiens, qui ne sont pas encore tous connus à l’époque (le texte d’Archimède qui en décrit treize a disparu et celui de Pappus, qui fait référence à Archimède, n’avait pas encore été édité). Pacioli pense même, à tort, que les solides semi-réguliers sont en nombre infini ; une raison pour lui de ne pas chercher à les trouver tous ! Ces polyèdres archimédiens sont le tétraèdre tronqué, l’octaèdre tronqué, l’icosaèdre tronqué, le cuboctaèdre et l’icosidodécaèdre (ces deux derniers sont vus comme cube tronqué et dodécaèdre tronqué), et une nouveauté, le petit rhombicuboctaèdre. Ces dénominations sont anachroniques : elles datent pour l’essentiel de Kepler. Enfin, Léonard montre en outre des prismes à bases triangulaire, carrée, pentagonale, hexagonale, et des pyramides à bases triangulaire, carrée, pentagonale et une sorte de géode. Le cube tronqué et le dodécaèdre tronqué, non décrits par Léonard, étaient connus de della Francesca ; l’icosidodécaèdre et le petit rhombicuboctaèdre semblent être décrits pour la première fois. Ce dernier deviendra l’emblème de Pacioli (voir en page 33, en haut à gauche du tableau).

Une polémique sur les modèles

Ces représentations de polyèdres interrogent les historiens des sciences : ont-ils été peints et dessinés d’après des modèles physiques ? Pacioli affirme que tous ont été construits. C’est vraisemblable : ils sont effectivement constructibles (contrairement aux patrons d’objets n’ayant aucune réalité constructible que l’on trouve chez d’autres auteurs de la Renaissance). La mode de l’intarsia laisse penser que de nombreux artisans étaient capables de les construire. La forme vacuus des modèles de Léonard n’est-elle pas directement la retranscription graphique de modèles en bois faits d’assemblages de barreaux ?

Plus troublant : si l’on consulte les trois versions connues du De Divina Proportione, c’est-à-dire  les manuscrits de Milan et de Genève et la version imprimée (éditée à Venise), on remarque que les polyèdres sont vus sous des angles judicieusement choisis. Comme si Léonard avait pu tourner autour de vrais modèles et sélectionner l’angle le plus seyant… À moins qu’il ait été doté d’un pouvoir de visualisation et d’abstraction lui permettant mentalement de trouver les meilleurs angles ? Dans les trois versions, les polyèdres sont vus sous des angles légèrement différents. Léonard aurait-il donc refait trois fois toutes ses constructions ?

Cependant, s’il avait dessiné ses figures suivant des modèles, il ne devrait y avoir aucune erreur dans ses schémas. Or, en étudiant de près le modèle du petit rhombicuboctaèdre elevatus, l’artiste Rinus Roelofs (né en 1954) s’est aperçu que plusieurs pyramides ne sont ni les bonnes, ni à la bonne place !

À gauche : Le pseudo petit rhombicuboctaèdre. À droite : Le petit rhombicuboctaèdre.

Le petit rhombicuboctaèdre, ce nouveau polyèdre de Luca Pacioli, est également à l’origine d’une polémique, toujours ouverte, sur le nombre de polyèdres archimédiens. En effet, en partant du solide qui possède la même symétrie que le cube et l’octaèdre, on peut par erreur faire tourner la coupe du bas de 45° et construire un nouveau solide, le pseudo petit rhombicuboctaèdre. Ce dernier répond à certaines définitions, locales, d’un polyèdre archimédien (à savoir : ses sommets sont sur une sphère, ses faces sont des polygones réguliers, et à chaque sommet se rencontrent les mêmes type et nombre de polygones). Mais il ne répond pas à une définition plus globale, qui est la transitivité des sommets (un groupe de symétrie permet de transformer n’importe quel sommet en tous les autres). Léonard a-t-il voulu représenter ce nouveau solide ? C’est la thèse de l’informaticien Carlo Heinrich Séquin. A-t-il reproduit un modèle assemblé avec une erreur ? Le mystère reste entier…

Les patrons, peu populaires…

Dans l’article New Light on the Rediscovery of the Archimedean Solids During the Renaissance, Peter Schreiber, Gisela Fischer et Maria Luise Sternath nous informent que les dessins de polyèdres vacuus sont tellement populaires que, dans les fac-similés et réimpressions, les autres dessins de Léonard ne sont plus reproduits. Or, à l’origine, il y avait aussi des patrons ! Ce fait, rarement signalé, est troublant. La plupart des auteurs considèrent que la première utilisation de patrons est celle d’Albrecht Dürer dans son Underweysung der Messung, mit dem Zirckel und Richtscheyt, in Linien ebnen und gantzen Corporen paru en 1525. Les patrons de Léonard semblaient-ils alors inintéressants ? Dans la planche représentée ici, on ne voit qu’un patron de dodécaèdre, agrémenté de quelques fioritures. Or, sur le dessin de Léonard, ce ne sont pas des fioritures… mais la construction du dodécaèdre camus ! Ce polyèdre est censé être inconnu à l’époque. L’utilisation de patrons pour construire de nouveaux polyèdres est, elle aussi, tout à fait innovante. Au XVI ^e siècle, l’usage des patrons était donc peut-être beaucoup plus répandu que ce l’on pensait. Et qui dit patron dit construction de modèles physiques !

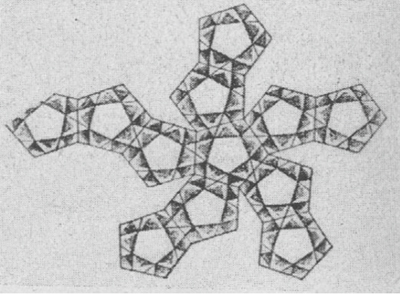
Patron du dodécaèdre camus de Léonard de Vinci dans De divina proportione.

D’autres polyèdres apparaissent dans les carnets de notes (ou codex) de Léonard. Son mode d’expression était essentiellement visuel. D’une page à l’autre, on saute d’un dessin de géométrie à une planche anatomique, voire à une étude pour tableau. Mais malgré cinq cents ans d’études, les spécialistes sont loin de tout connaître de son œuvre. Ce qui est maintenant certain, c’est que la connaissance de la géométrie et des polyèdres qu’avait Léonard de Vinci était remarquable pour son époque.

Le dodécaèdre camus.