Créer un monde virtuel nécessite déjà de représenter des formes, ainsi que leur apparence, et leur mouvement. Il faut ensuite simuler le voyage de la lumière jusqu'à l'œil via les objets de la scène ainsi éclairés. Et pour tout ça il faut… des maths (et de la physique, et de l'informatique, et parfois un peu de biologie aussi).

Modeler les formes

Vous avez déjà vu des images de maillages : on peut représenter la surface d'un objet comme un immense polyèdre irrégulier, à l'aide de facettes triangulaires ou quadrangulaires. Cependant, pour obtenir un aspect lisse, il faudrait des centaines de milliers de petites facettes, ce qui est très coûteux en mémoire. Voire, on aimerait adapter la quantité en fonction de la distance de l'objet à l'écran. De plus, l'artiste préfèrerait modeler avec des entités plus grandes, et plus souples que des facettes polygonales : il nous faut des éléments courbes. Comment faire ?

L'équivalent en 2D d'un maillage est une fonction affine par morceaux. Les courbes quant à elles correspondent à des fonctions, comme les polynômes. Pour tracer courbe tout en passant par des points clés (comme dans un logiciel de dessin vectoriel, de type Inkscape ou Illustrator), on utilise des polynômes par morceaux, choisis pour se recoller, pentes comprises. Quatre contraintes (deux hauteurs, deux pentes), cela nécessite un polynôme de degré 3, appelé fonction spline (voir les Algorithmes, Bibliothèque Tangente 37, 2013).

Pour se libérer de l'orientation imposée implicitement par une écriture du type y = f(x), on préfère exprimer les courbes en coordonnées paramétriques : on utilise un paramètre banalisé s à la place de l'abscisse x, et on utilise des vecteurs (position et tangente) à la place des scalaires (hauteurs et pentes) afin de faire bouger en même temps abscisses et ordonnées. Ce qui donne formellement P = f(s).

Pour passer au surfacique, donc à un « carreau spline », il suffit de voir ladite surface comme une nappe, c'est-à-dire une courbe glissant le long de rails courbes : des courbes splines « rail » dans une direction servent à définir les points de passage d'une courbe spline transverse glissant sur ces rails. La formule développée est en fait symétrique : on peut permuter les rôles des rails et de la courbe transverse glissante, ou encore voir cela comme un polynôme à deux paramètres, s et t, définis à partir de quatre points de contrôle, chacun constitué d'un sommet et de deux tangentes. On peut donc maintenant représenter les formes avec de vastes morceaux courbes.

Peindre l'apparence 

Qu'il soit à facettes ou courbe, un maillage reste un triste squelette : il faut habiller cette surface. Une couleur peut être représentée par trois composantes R (rouge), V (vert) et B (bleu). Mais où accrocher ces trois nombres ? Pas aux points clés, car on veut généralement peindre les surfaces avec une densité de points de couleur (une résolution) bien plus fine que le nombre de points clés définissant la géométrie. La solution consiste à tapisser la surface : on peint dans les pixels d'une image – la texture – destinée à être plaquée à la surface. Et plaquer, mathématiquement, c'est juste définir une injection de la surface vers l'image. Par exemple, pour texturer un carreau spline, on peut utiliser son paramétrage de surface (s, t) pour indiquer les coordonnées dans la texture : ainsi, tout point de la surface a un endroit dans la texture où l'on définit son apparence. Mais comme on ne veut pas se retrouver avec autant de bouts de texture qu'il y a de carreaux, et que l'on veut librement positionner la texture sur l'objet, on ajoute un système de coordonnées de texture (u, v) sur la surface, un mapping. Pour cela, il suffit d'en indiquer la valeur aux points clés, lesquels seront interpolés en même temps que la géométrie pour définir tout point de surface P(s, t). On n'a même pas forcément besoin d'une image explicite : toute fonction qui, à une coordonnée texture (u, v), retourne un triplet de couleurs (R, V, B), peut faire l'affaire. Ces textures procédurales permettent de créer un aspect riche à partir de quelques paramètres réglables.

Mais l'apparence ne se limite pas à une colorisation « plate » : on utilise des matériaux physiques, et ce sont tous leurs paramètres qu'il faut définir à la surface plutôt qu'un simple triplet (R, V, B). Ceux-ci peuvent inclurent une couleur diffuse, une couleur spéculaire, une rugosité, et bien d'autres coefficients, tous stockés en textures.

Mettre en vie : l'animation 

Animer, c'est déjà déplacer et tourner un personnage. Puis, hiérarchiquement : dans le repère du personnage, le bras peut lui-même tourner, et la main dans le repère du bras, et les doigts dans le repère de la main . La caméra elle-même a un repère qui peut être déplacé et tourné ; idem pour les sources de lumière. Pour unifier toutes ces transformations afin d'en faciliter le traitement, on les représente par des matrices 4 × 4, en coordonnées homogènes. Pourquoi ? Une rotation 2D se représente par une matrice 2 × 2, une rotation 3D par une matrice 3 × 3. Mais une matrice 4 × 4 permet de combiner rotations et translations, et plus encore ! Un point ordinaire est représenté en coordonnées homogènes, au départ, par ses trois coordonnées usuelles plus un poids égal à 1. Au final, on retrouvera le point 3D en divisant les trois premières coordonnées par le poids. La matrice

\( M=\left(\begin{array}{c c c|c} & & & \\ & R & & T \\ & & & \\ \hline 0 & 0 & 0 & 1 \end{array} \right)\)

(où R est une matrice de rotation 3 × 3 et T un vecteur de translation), multipliée à droite par le vecteur colonne 

\( \begin{pmatrix} P \\ 1 \end{pmatrix}\)

donne bien le point (RP + T, 1), tourné et translaté par rapport à P. En fait, les coordonnées homogènes permettent même de représenter la projection perspective à l'écran par une matrice : dans le cas canonique,  

\( M=\left(\begin{array}{c c c|c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \hline 0 & 0 & 1 & 0 \end{array}\right)\)

multipliée par 

\( \begin{pmatrix} P \\ 1 \end{pmatrix}" style="text-align: center;\)

donne 

\( \begin{pmatrix} P \\ z\end{pmatrix}\)

correspondant au point 3D de coordonnées (x / z, y / z , 1). L'avantage de cette représentation, c'est que la chaîne de transformations positionnant le doigt dans le monde s'obtient juste en multipliant les différentes matrices de changement de repère entre elles : composer, c'est multiplier. Et pour se ramener dans le repère de l'écran, perspective comprise, il suffit d'y combiner de surcroît l'inverse de celle positionnant la caméra dans le monde. Au final, il n'y a plus qu'à multiplier les points de la surface par une seule matrice pour trouver où ils se projettent à l'écran !

Animer, c'est aussi déformer. L'avantage de nos surfaces courbes, c'est qu'il suffit de déplacer-tourner les repères aux points clés pour déformer la surface. Mais ça reste laborieux (un personnage est fait de nombreux carreaux splines), et le graphiste préfère des contrôles plus intuitifs. Après tout, nous ne sommes pas des baudruches vides : la forme de notre peau s'appuie sur du muscle et suit les mouvements de notre squelette, entité plus naturelle à contrôler. Il est facile de modeler un squelette par des tiges articulées, mais comment « attacher » la surface à ce squelette ? Un indice : pour un bras rigide, il suffirait que sa géométrie soit décrite dans le repère de l'humérus, et ainsi le mouvement des points du bras se ferait en appliquant la matrice du repère de l'humérus. Mais un point proche du coude est attaché à la fois à l'humérus et au radius, son mouvement est un compromis entre les deux. Pour obtenir cela, la technique du skinning consiste à permettre d'associer plusieurs repères en même temps à un même objet, et d'indiquer pour chaque point le pourcentage de dépendance à chaque repère (attribut qui peut lui-même être peint dans une texture). Il suffit ensuite de combiner les transformations au prorata. 

Créer l'image : le rendu

En synthèse d'image réaliste, le rendu est obtenu en simulant la physique de la lumière, selon les lois de l'optique géométrique. Comme les chemins lumineux sont inversibles, il est équivalent et plus efficace de partir de la caméra virtuelle et de remonter la lumière jusqu'aux lampes (ou soleil) virtuels. L'algorithme du lancer de rayons consiste donc, pour chaque pixel de l'écran, à considérer le rayon partant du centre optique de l'œil et passant par le pixel, puis à déterminer ce qu'il voit en calculant l'intersection de cette demi-droite avec tous les objets de la scène, et même toutes les facettes de tous les objets de la scène, et enfin à trier tous ces points d'intersection par ordre de distance pour ne retenir que le plus proche. La texture permet alors de connaître la couleur de l'objet visible en ce pixel, mais ça ne suffit pas : d'une part, il faut savoir si cet endroit est éclairé ou à l'ombre, ce qui peut se faire en envoyant un rayon secondaire vers la lumière et en déterminant s'il intersecte un obstacle ou non. D'autre part, il faut tenir compte de la manière dont le matériau « prend la lumière » : un matériau mat renvoie la lumière identiquement dans toutes les directions, sachant qu'il la reçoit en fonction de son orientation (au prorata du cosinus de l'angle d'éclairement, obtenu par le produit scalaire entre la normale N à la surface et la direction L de la lumière), tandis qu'un matériau spéculaire la renvoie essentiellement autour de la direction miroir R (ce qu'on modélise en élevant le produit scalaire entre R et L à une puissance d'autant plus grande que le miroir est lisse, du moins pour les matériaux les plus simples). En outre, si une couche vernie ajoute un effet miroir, toute une réflexion de la scène se superpose à la couleur du matériau. Celle-ci est obtenue en envoyant un rayon secondaire dans une direction R (conformément à la loi de Snell-Descartes) pour déterminer ce qui y est vu. Pour un matériau transparent, on enverra de même un rayon réfracté dans la direction idoine.

De nos jours, on va plus loin dans la simulation : les sources de lumières ne sont pas ponctuelles mais larges, et « envoyer un rayon vers la lumière » correspond alors à une intégrale sur leur surface. De même, la lumière diffuse entre les murs par rebonds multiples : à chaque rebond, il faudrait donc envoyer des rayons secondaires dans toutes les directions (encore une intégrale). Et ainsi de suite pour intégrer tout le flux du transport radiatif reliant les sources de lumière à l'œil via les surfaces et leurs matériaux. Comme cette combinatoire est explosive, on utilise des méthodes d'intégration stochastiques, en s'efforçant de se concentrer sur les chemins lumineux susceptibles de rendre compte de l'essentiel de l'énergie transportée.

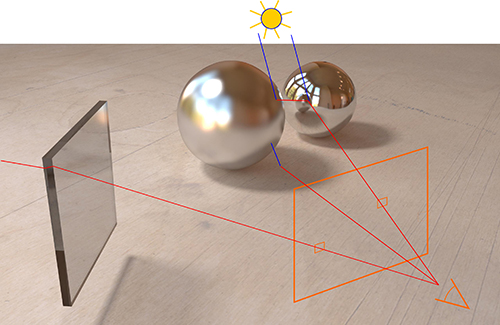
Pour deux pixels, rayon direct et rayon secondaire (lumière, reflets, réfraction)
permettant de déterminer la couleur à afficher.