Avez vous vu Avatar, réalisé par James Cameron (Twentieth Century Fox France, 2010) ? Dans ce film, comme d'ailleurs dans Shrek (Andrew Adamson et Vicky Jenson, 2001), Wall-E (Andrew Stanton, 2008), la Reine des neiges (Chris Buck et Jennifer Lee, 2013) et tant d'autres, on retrouve des animations faites par ordinateur. Quand on y pense, cela signifie que quelqu'un a créé une série d'instructions à envoyer à un ordinateur pour en arriver à ce produit fini.

Il ne s'agit pas là de faire dessiner une chaise ou une table ! On demande à un ordinateur de représenter un espace naturel, avec du relief et des personnages en mouvement. On ne peut évidemment pas se permettre de donner la position des pixels de couleur image par image, ce serait trop fastidieux et ingérable, tant en espace mémoire qu'en temps de traitement par la machine. On doit alors trouver une astuce permettant d'économiser du temps de calcul, sans quoi aucun ordinateur ne sera en mesure de compléter le travail.

La nature fractale du monde

Pour commencer, il semble plus simple de considérer un objet inanimé, une table par exemple. Ce meuble est bien défini : quatre pattes, un point de fuite, un plateau horizontal à une certaine hauteur, et un peu d'ombre permettent de le représenter. Mais qu'en est-il lorsque l'on prend un paysage comme ci-contre ? La complexité est telle que l'on ne sait même pas par où commencer !

L'idée est donc d'exploiter ces concepts mathématiques pour simplifier le nombre d'instructions nécessaires à la production d'images sophistiquées. Il devient alors possible de tirer profit de transformations géométriques pour reproduire des objets extrêmement détaillés avec très peu de consignes. Regardons le flocon de von Koch, et observons ce qui se trame avec un côté de cet objet étonnant.

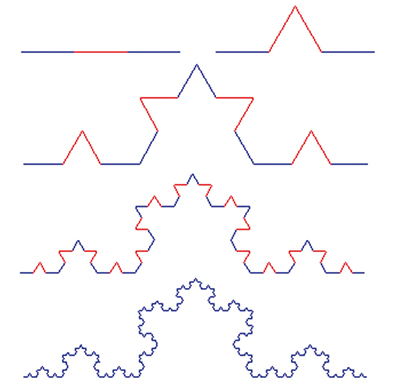
On prend un segment et on lui enlève le tiers du centre. Ensuite, on remplace ce tiers par deux tiers, que l'on dispose de telle sorte à obtenir une forme de triangle. Puis on recommence avec tous les côtés restants.

C'est cette « boucle sans fin » qui fait toute la magie ! Un ordinateur qui commence à traiter une image en se basant sur ces étapes ne terminera jamais le travail. Dans les cas réels, on doit spécifier une limite au programme (en pratique, moins de dix itérations suffisent pour obtenir un résultat spectaculaire).

On se retrouve, après une infinité d'étapes, avec un objet mathématique qui possède une surface finie (puisqu'il tient sur cette page) et un périmètre infini (puisqu'à chaque itération un segment voit sa longueur multipliée par 4/3).

Le même type de procédé peut être appliqué à partir d'un objet bidimensionnel. Vous pouvez d'ailleurs créer votre propre objet autosimilaire en allant sur le site Recursive Drawing. Des mathématiciens comme Karl Menger se sont même chargés d'imaginer de tels objets mathématiques en trois dimensions !

L'éponge de Menger.

Dans ce cas, le volume de l'objet est fini, alors que sa surface est infinie. C'est d'ailleurs une propriété qui est exploitée par l'un des organes du corps humain, le poumon. En effet, chaque bronche se sépare en plusieurs bronchioles qui possèdent plusieurs alvéoles, qui elles contiennent des capillaires. Ce sont ces capillaires qui assurent le transfert d'oxygène entre l'air aspiré et le sang qui circule dans nos veines (voir Mathématiques et Chimie, Bibliothèque Tangente 43). La surface de nos poumons est si grande que si on pouvait étendre entièrement nos poumons sur le sol, ils pourraient couvrir l'équivalent d'un terrain de tennis complet. Ce n'est pas exactement une surface infinie, mais cela suffit pour nos besoins.

De l'avion à l'animation

L'instigateur de l'utilisation des fractales dans l'animation d'images est Loren Carpenter. Bien qu'il soit aujourd'hui connu pour être l'un des cofondateurs du studio d'animation Pixar, il était à l'époque employé du département de services informatiques de Boeing. Un jour, on lui fait la demande de réaliser un paysage pour mettre en avant un nouvel avion. Une telle demande peut paraître ridicule aujourd'hui, mais elle permettait à l'époque d'économiser le vol simultané de deux avions (le nouvel avion et celui utilisé pour prendre le cliché). Cette image permettait donc de réduire de manière phénoménale les coûts de publicité… et de limiter les risques d'accident.

Carpenter sillonne les bibliothèques à la recherche d'informations. C'est ainsi qu'il tombe sur l'ouvrage phare de Benoît Mandelbrot, Forme, Hasard et Dimensions (Flammarion, 2010). Dans ce livre, on trouve une réflexion mathématique sur des questions pratiques (combien mesure la côte de la Bretagne ?). De plus, il est peuplé d'objets mathématiques aux allures réalistes. Une mine d'or pour orienter un informaticien dans ses efforts de programmation !

Loren Carpenter releva ainsi le défi de créer une image pour la compagnie Boeing. Il réalisa la toute première animation, en se basant sur l'idée des fractales, le court métrage Vol libre (John Lewis et L. Carpenter, 1980).

Ce tour de force met immédiatement la puce à l'oreille de la division informatique de Lucasfilm, où Carpenter peut poursuivre le développement de son logiciel Genesis Effect. Deux ans plus tard, on verra apparaître une scène entièrement générée par ordinateur, dans le film Star Trek II: The Wrath of Khan (Nicholas Meyer, 1982). Quelques années après, cette division deviendra la maison de production Pixar.

Depuis, le progrès ne s'est jamais arrêté, si bien qu'il est devenu difficile de déterminer si certaines images ou scènes sont réelles ou générées par ordinateur…