L'importance du problème de la quadrature de l'hyperbole a été affirmée par Marin Mersenne au début du XVIIe siècle. En langage moderne, il s'agit pour l'essentiel de déterminer la mesure de l'aire A(a) que délimitent la courbe H d'équation y = 1/x, l'axe (Ox) des abscisses, la verticale d'abscisse 1 et une autre verticale d'abscisse a quelconque.
Au début du XVIIe siècle, il y a plusieurs bonnes raisons pour s'intéresser à ce problème. La première est que l'hyperbole est l'une des trois « sœurs coniques » (avec l'ellipse et la parabole), qui sont des courbes connues et utilisées depuis l'Antiquité et dont l'intérêt scientifique vient soudain de déborder bien au-delà de la seule géométrie. Quelques années plus tôt en effet, Galilée a découvert que, sur Terre, la trajectoire d'un projectile non soumis à des frottements est une parabole, tandis que Johannes Kepler a proposé de rendre compte du mouvement des planètes à l'aide d'ellipses.
Une autre raison plus mathématique à l'intérêt pour l'hyperbole est que Pierre de Fermat vient de réaliser la quadrature de toutes les courbes de la forme y = xu. En langage moderne, il a trouvé une expression explicite pour une primitive de la fonction f(x) = xu ; c'est la fameuse formule xu+1/(u+1), valable pour toutes les valeurs de u… à la seule exception du cas u = –1, celui de l'hyperbole, pour lequel cette formule n'a pas de sens.
Nargués par l'hyperbole
Peut-être agacés d'être ainsi nargués par cette valeur rebelle, Grégoire de Saint-Vincent et sont élève Alfonso Antonio de Sarasa s'attaquent au problème entre 1647 et 1649. À l'aide d'un raisonnement géométrique extrêmement élégant, ils réalisent le premier pas significatif vers une compréhension de l'importance fondamentale des logarithmes en mathématiques, un siècle avant la synthèse qui sera finalement faite par Leonhard Euler.
Considérons la branche positive, celle du quadrant supérieur droit, de l'hyperbole H d'équation y = 1/x dans un repère cartésien ordinaire. Intéressons-nous aux transformations du plan qui laissent H globalement invariante, c'est-à-dire que chaque point de H est déplacé par ces transformations sur d'autres points eux aussi sur H. Soit b > 0. Notons Tb la transformation qui envoie le point de coordonnées (x, y) sur le point de coordonnées (x/b, by). En quelque sorte, on a affaire à une homothétie de rapport 1/b dans le sens des x et à une homothétie de rapport b dans le sens des y. Cela revient à « contracter » les figures d'un facteur b dans la direction horizontale, et à les « dilater » du même facteur b dans la direction verticale. Alors, quel que soit b, l'hyperbole H est globalement invariante par Tb : le point (x, 1/x) de H est envoyé sur (x/b, b/x), qui est bien lui aussi sur H.
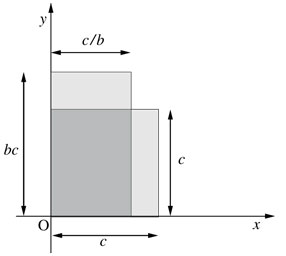Une propriété cruciale des transformations Tb est qu'elles préservent les aires. Cela peut sembler étonnant dans la mesure où les Tb ne préservent pas les longueurs, ni les formes des figures. Voici pourtant un élément de démonstration. Sous l'effet de Tb, un carré de côté c orienté selon les axes du repère est transformé en un rectangle de côtés c/b et bc, dont l'aire est (c/b)(bc) = c2, qui est bien égale à celle du carré initial. Ce qui est perdu par une dimension est donc très exactement compensé par ce qui est gagné par l'autre.
Vers une relation fondamentale
Munis de ces transformations Tb, on peut à présent étudier l'aire sous l'hyperbole. Considérons deux nombres a et b supérieurs à 1 et intéressons-nous à la valeur de l'aire A(ab) définie par le domaine limité par H, (Ox) et les droites d'équation x = 1 et x = ab. Les points de coordonnées (1, 1) et (ab, 1/(ab)) sont notés U et V.
Appliquons à présent la transformation Tb à cette figure. Les points U et V sont envoyés sur Tb(U) et Tb(V), de coordonnées (1/b, b) et (a, 1/a). Par préservation des aires, l'aire du nouveau domaine est égale à l'aire initiale, soit A(ab).
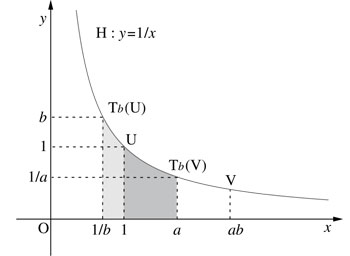
La droite verticale passant par U partage notre nouveau domaine en deux morceaux. L'aire du morceau de droite, limité par U et Tb(V), est par définition égale à A(a). Reste à estimer celle de gauche. Pour cela, appliquons lui la transformation T1/b (qui n'est autre que la réciproque de Tb). Le point Tb(U) est renvoyé sur U, tandis que le point U est envoyé sur le point de coordonnées (b, 1/b).
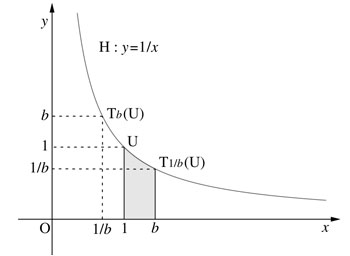
L'aire ainsi délimitée, qui est égale à celle de notre morceau de gauche précédent, est donc égale à A(b).
Ainsi, pour tous a et b plus grands que 1 (mais ce qui suit est en réalité valable pour tous a > 0 et b > 0), on a la relation fondamentale : A(ab) = A(a) + A(b).
C'est précisément la relation qui définit les fonctions logarithmes ! Il resterait encore à déterminer de laquelle il s'agit, c'est-à-dire la valeur (aujourd'hui notée e) telle que A(x) = loge(x) pour tout x.
Il faut attendre Euler, un siècle plus tard, pour que ce dernier point soit éclairci. Toutefois, même sans la mise au jour de e, le résultat de Saint-Vincent et de Sarasa est déjà d'une portée considérable. En faisant apparaître la relation fonctionnelle A(ab) = A(a) + A(b) au cœur du calcul de l'intégrale de 1/x, ce résultat marque l'irruption définitive des logarithmes dans l'analyse mathématique, jetant ainsi un pont à jamais incontournable entre l'algèbre et l'analyse.
Lire la suite