Les étonnantes inventions de John Neper

Né en Ecosse en 1550 dans une famille de grands propriétaires terriens, John Neper, version francisée du nom Napier (pour qu'en France, on prononce son nom comme outre-Manche…), sorti sans diplôme de l'université de Saint-Andrews, protestant convaincu, auteur d'un ouvrage de théologie violemment antipapiste, n'était pas à proprement parler mathématicien. Cherchant à faciliter le travail des navigateurs et astronomes, préoccupé de trigonométrie sphérique, il est l'auteur d'un aide-mémoire pour la résolution des triangles sphériques et de quelques formules connues sous le nom d'analogies de Napier ; pas de quoi passer à la postérité. Sa renommée, il la doit à sa géniale intuition d'avoir inventé de quoi révolutionner le calcul : les logarithmes.

Vingt ans de logarithmes

Comme le seront après lui Pierre de Fermat (vers 1601–1665), Thomas Bayes (vers 1702–1761) ou Gottfried Leibniz (1646–1716), John Neper était au départ un amateur éclairé de mathématiques. Il avait fait de cette discipline non pas sa profession, mais son passe-temps favori, et ce dans le souci d'alléger le travail de tous les calculateurs.

« Il n'y a rien de plus pénible, dans la pratique des mathématiques, […] que ces multiplications, divisions, extractions de racines carrées et cubiques de grands nombres, qui, à côté d'une assommante perte de temps, engendrent pour la plupart nombre d'erreurs insaisissables. […] Remplaçons les nombres par d'autres, qui fonctionneront seulement par addition et soustraction, division par deux ou par trois. »

Inspiré par la formule : sin(a) sin(b) = (1/2) cos(a – b) – (1/2) cos(a + b), il cherche donc à exprimer un produit de deux facteurs sous forme de somme et plus généralement à utiliser une telle relation pour simplifier les calculs. L'idée n'est pas neuve, elle a déjà été utilisée par les astronomes arabes du XI^e siècle ; elle a aussi inspiré l'horloger suisse créateur d'instruments Jost Bürgi (1552–1632), qui avait conçu vers 1610 une table de correspondance entre une suite arithmétique et une suite géométrique.

C'est alors qu'en 1614, John Neper publie en latin Mirifici logarithmorum canonis descriptio, où il introduit la notion de logarithme (de logos, « rapport » et arithmos, « nombre ») par une approche mécanique. Il rentre largement dans les détails.

Il choisit un segment [AB] de longueur qu'il fixe à 10⁷ et, parallèlement, une demi-droite [A'X) allant à l'infini. Les points C et C', avec la même vitesse initiale, se déplacent simultanément, le premier de A vers B avec une vitesse proportionnelle à la distance CB restant à parcourir, le second de A' vers X avec une vitesse uniforme. Neper établit une relation entre y, représenté par A'C', et x, représenté par BC, et pose tout de go y = Nap.log x, mettant en correspondance une suite arithmétique de premier terme 0 et de raison 1 (celle des logarithmes) et une suite géométrique de premier terme 10⁷ et de raison  \( {\dfrac{10^7-1}{10^7}},\)   c'est-à-dire    \( 1-{\dfrac{1}{10^7}}.\)  

Le point C se déplace avec une vitesse proportionnelle à BC de A vers B (AB = 10⁷). Dans le même temps, le point C' se déplace à vitesse constante. 

Pour Neper, x représente d'ailleurs le sinus d'un angle. C'est pourquoi il parle la plupart du temps de « logarithmes de sinus », et « son » sinus (noté Sin) est la demi-corde correspondant à un angle X dans un cercle de rayon 10⁷. Ceci signifie x = 10⁷Sin X et il a choisi 10⁷ car, pensait-il, les meilleures tables de sinus offrent une précision de sept décimales.

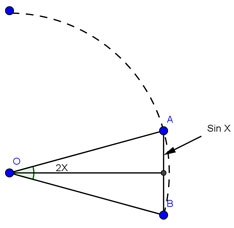
Le sinus x = AC de Napier est la demi-corde correspondant à l'angle X. 

Comme OA = OB = 10⁷, 

Sin(0°) = 0 

et Sin(90°) =10⁷.

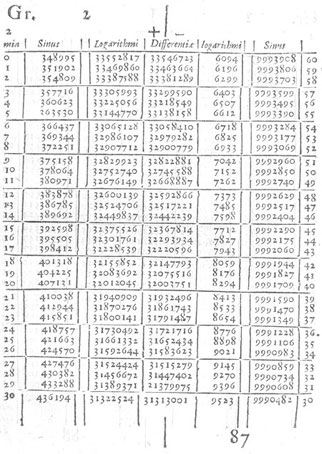
La première table de logarithmes de Neper donne donc les valeurs successives, pour n allant de 10⁷ à 1, des termes de la suite définie par \( 10^7\left(1-{\dfrac{1}{10^7}}\right)^n\)   ainsi que des angles associés, de minute en minute. C'est l'auteur lui-même qui a ainsi tabulé « ses » logarithmes pour ces dix millions de valeurs (!), ce qui, disait-il, lui a pris vingt années de sa vie, mais vingt ans… pour épargner du temps à d'autres calculateurs. D'autres tables vont suivre, construites sur des subtilités de calcul de plus en plus raffinées.

La table de logarithmes de Neper.

Évidemment, ces logarithmes définis par Neper ne sont pas « nos » logarithmes habituels, ils ne sont pas définis par rapport à une « base » (nombre dont le logarithme est égal à 1), et ne vérifient pas non plus Nap.log 1 = 0, ce qui ne facilite pas toujours les choses dans les calculs… 

C'est le mathématicien britannique Henri Briggs (1556-1630) qui le fait remarquer à Neper lors de leur rencontre à l'été 1615, lui suggérant de construire de nouvelles tables, cette fois d'un logarithme de base 10, avec log 1 = 0. Briggs lui-même construisit de telles tables. Il revoit Neper en 1616. Le décès de Neper en 1617 a empêché leur troisième rencontre.

Nous utilisons aujourd'hui le logarithme népérien, défini à partir de la quadrature de l'hyperbole et possédant des propriétés algébrique analogues, mais ce n'est pas le « Nap.log » du mathématicien écossais ; ce nom est seulement un hommage à Neper.

Un bricoleur mathématique de génie 

Neper a été, à plus d'un titre, un génie inventif. Déjà, on sait que y = Nap.log x revient à dire que  \( x=10^7\left(1-{\dfrac{1}{10^7}}\right)^y\) ; sa découverte permet de répondre à la question suivante : pour un nombre y donné, quel est le nombre x dont il est le logarithme ? Mais surtout, Neper lui-même a, dans le Livre second de sa Descriptio, décrit minutieusement, exemples à l'appui, « l'emploi efficace dans la trigonométrie de la merveilleuse table des logarithmes ». 

L'un de ses exemples parle de lui-même : on donne un triangle ABC où AB = 26 302, BC = 57 955 et l'angle en C est de 26°. Il s'agit de calculer l'angle en A sachant qu'il est aigu. Avec force détails, l'auteur donne la marche à suivre : 
utiliser la relation  

\( {\dfrac{\text{AB}}{\sin \widehat{\text{C}}}}= {\dfrac{\text{BC}}{\sin \widehat{\text{A}}}},\)  

puis passer aux logarithmes, d'où

Nap.log sin( \( \widehat{\text{A}}\) ) = Nap.log BC + Nap.log sin( \( \widehat{\text{C}}\)  ) – Nap.log AB,

et enfin utiliser « sa » table pour trouver

Nap.log sin( \( \widehat{\text{A}}\) ) = 346 675.

Comme on lit, toujours dans la table, Nap.log(Sin 75) = 346 683, on conclut que \( \widehat{\text{A}}\)  =75° environ.

Familier de la trigonométrie du triangle, Neper l'était certainement, mais il l'était aussi de la trigonométrie sphérique, au point d'avoir là aussi laissé son nom à un ensemble de formules relatives à un triangle sphérique de côtés a, b, c et d'angles  \( \widehat{\text{A}},\)   \( \widehat{\text{B}},\)   \( \widehat{\text{C}}\)  qui leur sont respectivement opposés. Ces quatre identités sont connues sous le nom d'analogies de Napier :

\( $${\dfrac{\sin \left({\dfrac{1}{2} ({\widehat{\text{A}}- {\widehat{\text{B}}})}}\right)} {\sin \left({\dfrac{1}{2} ({\widehat{\text{A}}+ {\widehat{\text{B}}})}}\right)}} = {\dfrac{\tan \left({\dfrac{1}{2} {(a- b})}\right)} {\tan \left({\dfrac{1}{2} c}\right)}}, $$\)   

  \( $${\dfrac{\cos \left({\dfrac{1}{2} ({\widehat{\text{A}}- {\widehat{\text{B}}})}}\right)} {\cos \left({\dfrac{1}{2} ({\widehat{\text{A}}+ {\widehat{\text{B}}})}}\right)}} = {\dfrac{\tan \left({\dfrac{1}{2} {(a+ b})}\right)} {\tan \left({\dfrac{1}{2} c}\right)}}, $$\)  

\( $${\dfrac{\sin \left({\dfrac{1}{2} (a-b)}\right)} {\sin \left({\dfrac{1}{2} (a+b)}\right)}} = {\dfrac{\tan \left({\dfrac{1}{2} ({\widehat{\text{A}}- {\widehat{\text{B}}})}}\right)} {\cot \left({\dfrac{1}{2} {\widehat{\text{C}}}}\right)}}, $$\)  

\( $${\dfrac{\cos \left({\dfrac{1}{2} (a-b)}\right)} {\cos \left({\dfrac{1}{2} (a+b)}\right)}} = {\dfrac{\tan \left({\dfrac{1}{2} ({\widehat{\text{A}}+ {\widehat{\text{B}}})}}\right)} {\cot \left({\dfrac{1}{2} {\widehat{\text{C}}}}\right)}}. $$\)

 Le souci constant de Neper de faciliter la tâche aux calculateurs ne s'arrête pas là : il est ainsi le premier à utiliser la notation décimale avec point (notre virgule) pour les nombres fractionnaires, écrivant par exemple 1615,384 au lieu de  \( $$1615\dfrac{384}{1000} $$\) .

Il crée également des réglettes qui portent son nom (les fameux bâtons de Neper), préfigurant les premières machines à calculer mécaniques, qu'il présente dans l'un de ses autres ouvrages, publié en 1617, Rabdologiae.

Boîte de bâtonnets de Neper à quatre faces.

De construction très simple, ces « bûchettes » vont permettre, sans calcul, de donner le résultat d'une multiplication, comme celle de 966 975 par 6. On aligne de gauche à droite les bâtons « 9 », « 6 », « 6 », « 9 », « 7 », « 5 » sur lesquels on lit, ligne 6 :

Ce qui donne immédiatement le résultat, par addition des nombres contigus (ne pas oublier la retenue !) : 5 801 850. Il suffisait d'y penser !

John Neper a indiscutablement laissé une trace dans l'histoire, non seulement dans celle du calcul en imaginant les logarithmes, qualifiés par Pierre-Simon de Laplace en 1795 « d'admirable instrument qui, en réduisant à quelques heures le travail de plusieurs mois, double si l'on peut dire la vie des astronomes », mais dans l'histoire des mathématiques en général, avec toutes les perspectives, comme l'exponentielle, réelle ou complexe, que la fonction logarithme a permis d'ouvrir.